代码随想录算法训练营第60期第六十二天打卡

        大家好，我们昨天主要讲解了求解最小生成树的两种算法，今天我们就继续我们的图论部分，我们今天的主题主要是最短路算法，其中有一个最短路算法是非常有名的，叫做Dijkstra算法，我们今天就主要讲解拓扑排序与最短路算法。

第一部分 拓扑排序

       我们今天就主要讲解拓扑排序的理论基础与代码实现，我们先不刷题，我们要先充分理解好这个算法以后再去刷题，一聊到 拓扑排序，大家可能会想这是排序，不会想到这是图论算法。其实我第一次听说到拓扑排序的时候也是觉得这应该是属于排序算法，而在C++里我们有STL，其实排序是不难实现的，我们先说说 拓扑排序的应用场景。

        例如大学排课，例如 先上A课，才能上B课，上了B课才能上C课，上了A课才能上D课，等等一系列这样的依赖顺序。 问给规划出一条 完整的上课顺序。拓扑排序在文件处理上也有应用，我们在做项目安装文件包的时候，经常发现 复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。其实我们目前举的例子都比较简单，大家或许很轻松就可以看出，但是如果规模大了呢？大家是否还可以看出来？其实拓扑排序解决的就是这种问题，概括来说，给出一个 有向图，把这个有向图转成线性的排序 就叫拓扑排序。当然拓扑排序也要检测这个有向图 是否有环，即存在循环依赖的情况，因为这种情况是不能做线性排序的。所以拓扑排序也是图论中判断有向无环图的常用方法。

        接下来我们重点看拓扑排序的思路，其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。大家不需要去纠结这个问题。这里我们主要讲的是BFS，在这里BFS比较清晰易懂，我们可以看一下下面的图：

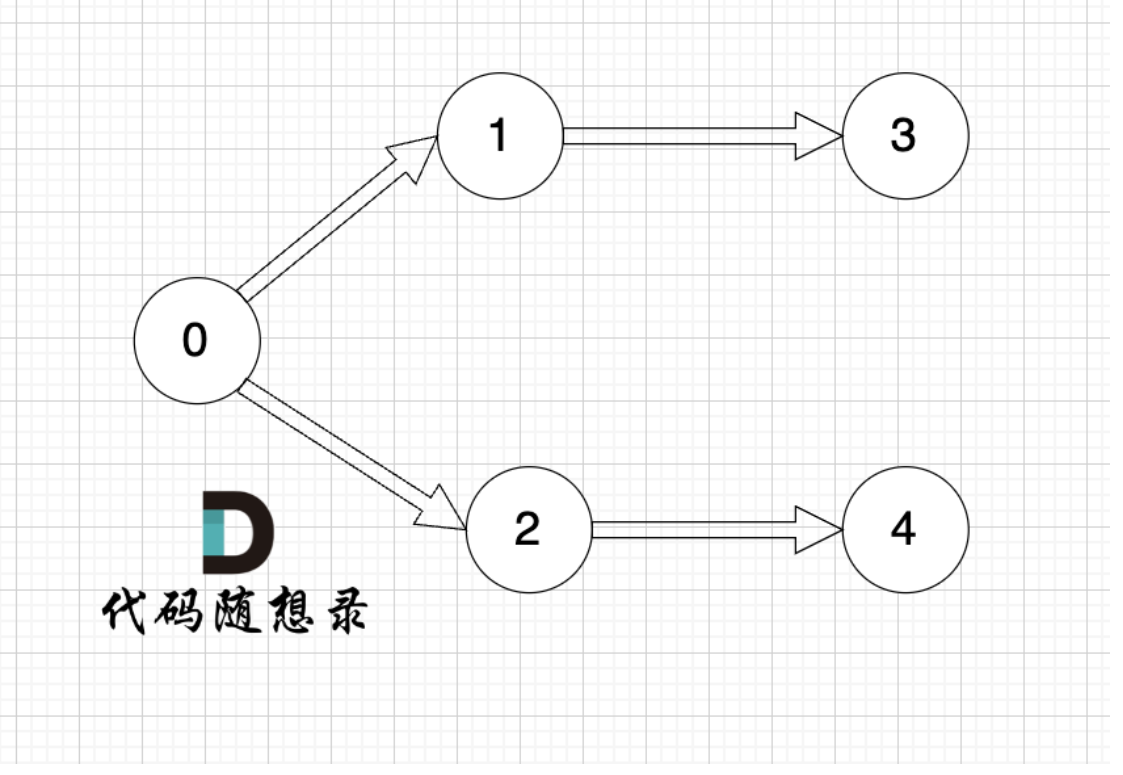
       其实相信大家可以很轻松看出来我们这个图的起点是节点0，但是我们这只是图上看出来的而已，我们要找到有说服力的依据才可以，其实我们可以看到我们的节点0入度为0而出度为2，这就表明不存在指向节点0的边但是节点0却可以指向其他的节点，所以当我们做拓扑排序的时候，应该优先找 入度为 0 的节点，只有入度为0，它才是出发节点。其实我们拓扑排序的过程就两步，第一步就是找到入度为0 的节点，加入结果集，第二步是将该节点从图中移除，我们一直循环如下两步其实就可以将所有节点都在图中移除了。结果集的顺序，就是我们想要的拓扑排序顺序 （结果集里顺序可能不唯一）。我们就不模拟这个过程了，其实大家也可以意识到方法是不止一种的，但是有一点我是一定要说明的，就是如果图中有环应该如何处理？大家可以看下图：

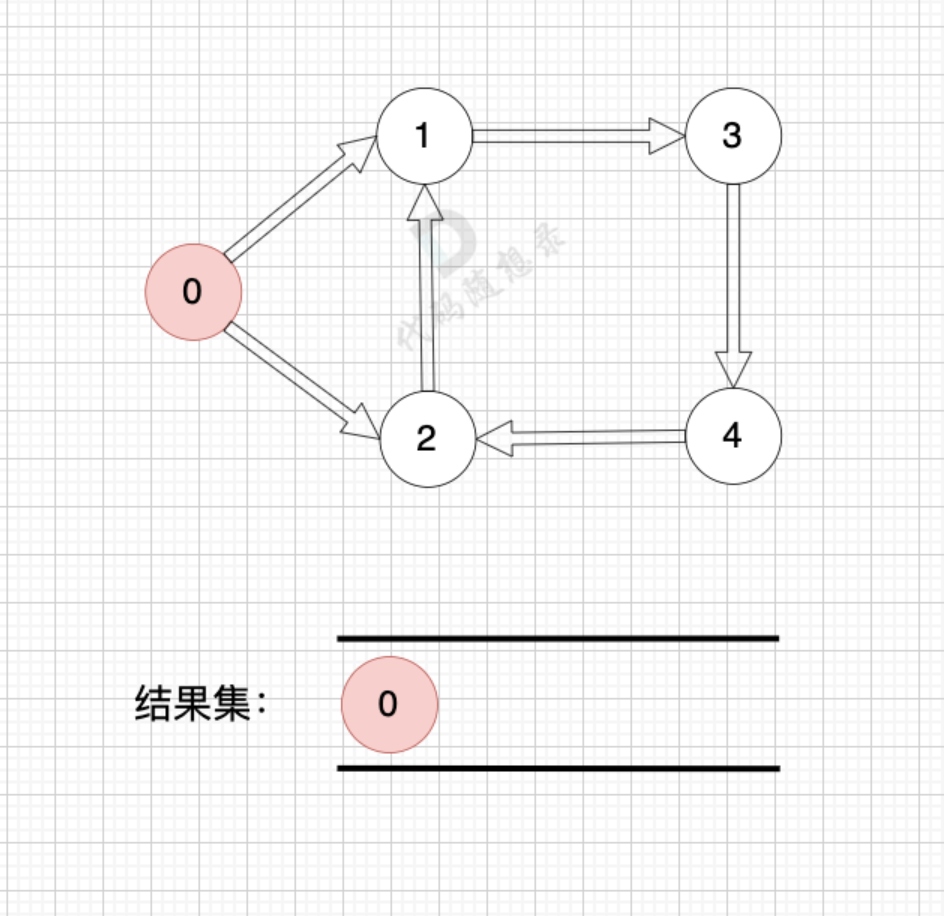
       有环的话，我们可以看到我们找到了入度为0的节点，我们加入结果集并将其在图中删除，我们就会发现我们接下来就找不到入度为0的节点了，那么如果我们发现结果集元素个数 不等于 图中节点个数，我们就可以认定图中一定有 有向环！这也是拓扑排序判断有向环的方法。

       综上，大家会觉得这个算法也不难，其实的确不难，那我们就可以尝试写代码来实现这个算法了：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
int main() {int m, n, s, t;cin >> n >> m;vector<int> inDegree(n, 0); // 记录每个文件的入度unordered_map<int, vector<int>> umap;// 记录文件依赖关系vector<int> result; // 记录结果while (m--) {// s->t，先有s才能有tcin >> s >> t;inDegree[t]++; // t的入度加一umap[s].push_back(t); // 记录s指向哪些文件}queue<int> que;for (int i = 0; i < n; i++) {// 入度为0的文件，可以作为开头，先加入队列if (inDegree[i] == 0) que.push(i);//cout << inDegree[i] << endl;}// int count = 0;while (que.size()) {int  cur = que.front(); // 当前选中的文件que.pop();//count++;result.push_back(cur);vector<int> files = umap[cur]; //获取该文件指向的文件if (files.size()) { // cur有后续文件for (int i = 0; i < files.size(); i++) {inDegree[files[i]] --; // cur的指向的文件入度-1if(inDegree[files[i]] == 0) que.push(files[i]);}}}if (result.size() == n) {for (int i = 0; i < n - 1; i++) cout << result[i] << " ";cout << result[n - 1];} else cout << -1 << endl;}

        其实大家看完代码应该也不难理解，我们就是找度为0的节点，然后去找与这个节点相邻的节点，其实代码也不难理解了，最后大家注意我们没有环的情况下才可以得到完整的拓扑排序，一旦没有得到完整的拓扑排序我们就可以断定这个图是存在环的。关于拓扑排序我们就分享这么多，我们接下来看我们的最短路问题。

第二部分 dijkstra（朴素版）

        接下来来到我们的dijkstra算法，我们这个最短路算法其实有两种版本，一种叫做朴素版，另一种叫做堆优化版本，我们今天主要讲解朴素版的版本，明天我们讲解堆优化版本，最短路算法其实是给出一个有向图，一个起点，一个终点，问起点到终点的最短路径。我们就引入最流行的dijkstra算法：在有权图（权值非负数）中求从起点到其他节点的最短路径算法。但是大家需要注意dijkstra 算法可以同时求 起点到所有节点的最短路径。而且权值不能为负数。

        我们首先给出dijkstra三部曲：第一步，选源点到哪个节点近且该节点未被访问过，第二步，该最近节点被标记访问过，第三步，更新非访问节点到源点的距离（即更新minDist数组），那么就有一个数组非常重要就是minDist。minDist数组 用来记录 每一个节点距离源点的最小距离。其实我们也知道这个最小距离是会不断更新的。

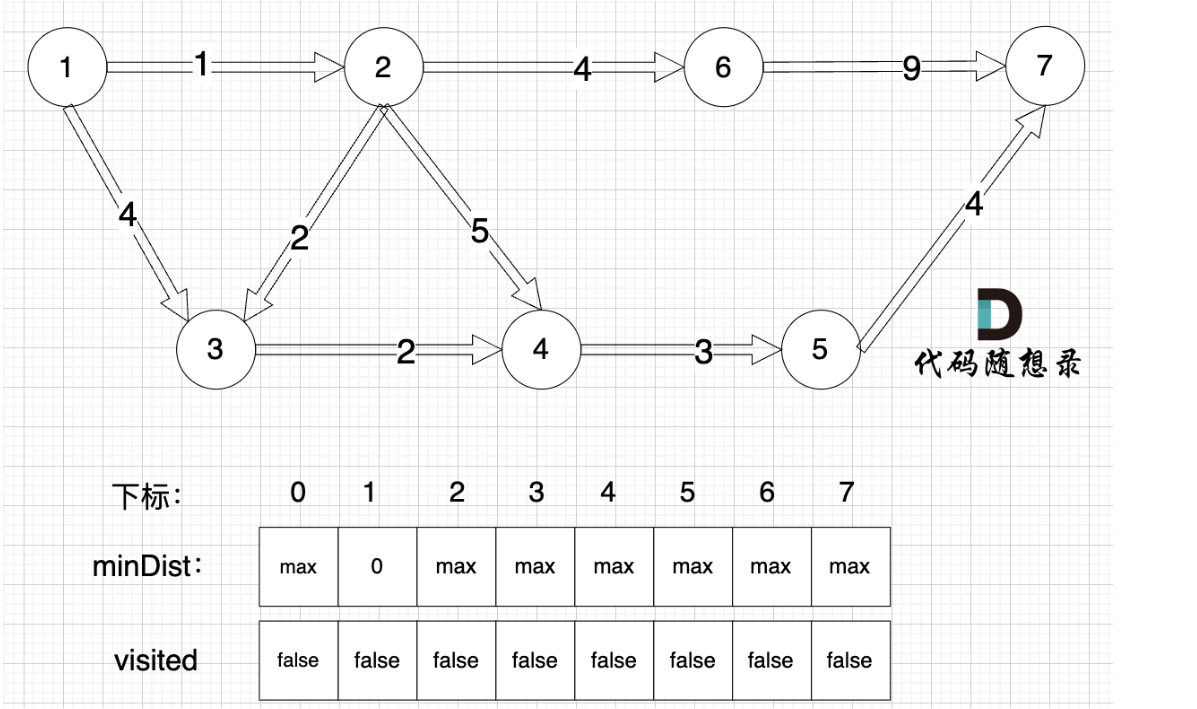
         大家可以看上面的图示，我们初始是将起点与其他各个点的距离设置为无穷大，我们的visited数组设置都未访问过，图中，max 表示默认值，节点0 不做处理，统一从下标1 开始计算，这样下标和节点数值统一。首先源点（节点1） 到自己的距离为0，所以 minDist[1] = 0，接下来根据三部曲更新 minDist数组，即：源点（节点1） 到 节点2 和 节点3的距离。我们可以看到源点到节点2的最短距离为1，小于原minDist[2]的数值max，更新minDist[2] = 1，源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[3] = 4，同时节点2被标记访问过，因为目前来说节点2是距离起点最近的，接下来的思路与之类似，更新 minDist数组，即：源点（节点1） 到 节点6 、 节点3 和 节点4的距离。至于为什么更新这些节点是因为 源点（节点1）通过 已经计算过的节点（节点2） 可以链接到的节点 有 节点3，节点4和节点6。则源点到节点6的最短距离为5，小于原minDist[6]的数值max，更新minDist[6] = 5，源点到节点3的最短距离为3，小于原minDist[3]的数值4，更新minDist[3] = 3，源点到节点4的最短距离为6，小于原minDist[4]的数值max，更新minDist[4] = 6。接下来的过程与之类似，我们就是一直更新最短路径，直到找到终点结束。

     那么我们就可以考虑用代码来实现：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {int n, m, p1, p2, val;cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));for(int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid[p1][p2] = val;}int start = 1;int end = n;// 存储从源点到每个节点的最短距离std::vector<int> minDist(n + 1, INT_MAX);// 记录顶点是否被访问过std::vector<bool> visited(n + 1, false);minDist[start] = 0;  // 起始点到自身的距离为0for (int i = 1; i <= n; i++) { // 遍历所有节点int minVal = INT_MAX;int cur = 1;// 1、选距离源点最近且未访问过的节点for (int v = 1; v <= n; ++v) {if (!visited[v] && minDist[v] < minVal) {minVal = minDist[v];cur = v;}}visited[cur] = true;  // 2、标记该节点已被访问// 3、第三步，更新非访问节点到源点的距离（即更新minDist数组）for (int v = 1; v <= n; v++) {if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {minDist[v] = minDist[cur] + grid[cur][v];}}}if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点else cout << minDist[end] << endl; // 到达终点最短路径}

      大家注意我们这个算法并不适合边权存在负数的情况，我们后面会讲解解决边权为负数的最短路算法，大家目前先把这个理解好。

今日总结

        今天我们主要讲解了拓扑排序与最短路算法，其实算法实现起来还是有难度，大家一刷的时候大致理解好算法的基本思想就可以了，没必要去深究，我们今天就讲解到这里，我们下次博客再见！