二水平设计的单次重复
本文是实验设计与分析(第6版,Montgomery著傅珏生译)第6章2k析因设计第6.5的python解决方案。本文尽量避免重复书中的理论,着于提供python解决方案,并与原书的运算结果进行对比。您可以从Detail 下载实验设计与分析(第6版,Montgomery著傅珏生译)电子版。本文假定您已具备python基础,如果您还没有python的基础,可以从Detail 下载相关资料进行学习。
即使是对于中等大小的因子个数,2k析因设计的处理组合的总数也是很大的。例如,25设计有32个处理组合,26设计有64个处理组合等。因为资源通常受限,实验者能做的重复次数也就受到限制。通常可用的资源只允许对设计做一次重复,除非实验者愿意消去某些原来的因子。
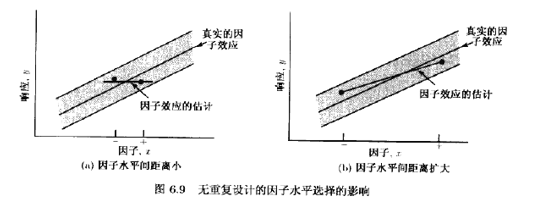
每个试验组合仅进行一次实验的风险是,我们可能拟合了含噪声的模型。即,若响应y变化程度大,这可能会误导从实验中得到的结论。如图6.9a所示。该图中,直线代表真实的因子效应。但是,由于出现在响应变量(用阴影带表示)中的随机变异性,实验者得到了用照圆点表示的两个测量到的响应。于是,因子效应的估计接近于零。结果,实验者得到了关于该因子的错误结论。如果响应的变化程度较小,错误结论的可能性也会较小,另一种确保得到可靠的效应估计的方法是增加低(-)水平和高(+)水平因子间的距离,如图6.9b所示。该图中,低因子水平和高因子水平间的增加了的距离得到了真实因子效应的合理估计。
一次重复策略通常用于有相对多的需考虑因子的筛选实验。因为,我们在不能完全确信实验误差小的情形下,采取尽量拉开因子水平是一个好的做法,重读第1章中选择因子水平的指南,也许会有帮助
2k设计的单次重复有时称为无重复的析因设计,因为仅有一次重复,所以没有误差的内在估计(即“纯误差”)。无重复析因设计的一种分析法是,假定某些高阶的交互作用可被忽略,并将它们的均方组合起来用于估计误差.这要借助于效应稀疏原理(sparsity of effect principle),也就是,很多系统的一些主效应和低阶的交互作用处于支配地位,而很多高阶交互作用可被忽路。
当分析无重复析因设计的数据时,有时出现真正的高阶交互作用。此时,将高阶交互作用集中起来作为误差均方使用是不恰当的。Daniel(1959)提出的分析方法是克服这一困难的简便途径。Daniel建议,检查效应估计量的正态概率图。可被忽略的效应是正态分布的,其均值为零方差为σ2,因此会大致落在图上的一条直线附近;而显著效应有非零均值因此不会落在这一直线上。因此,基于正态概率图,初始模型必须指定包含那些显显不为零的效应。显然可以将忽略的效应组合成误差的估计。
例6.2 24设计的单次重复
一种化学产品是在压力容器中生产的。在一个小规模的试验性工厂中进行一项析因实验,用以研究可能会影响这种产品浅透率的因子,4个因子是温度(A)、压强(B),甲醛浓度(C)和搅拌速度(D)。每一因子取两个水平,
24试验的单次重复所得的数据如:表6.10和图6.10所示。依随机次序进行16次试验。工程师感兴趣的是使渗透率达到最大。在当前的生产条件下,产品的渗透率钓为75gal/h(加仑/小时)。当前生产用的甲醛浓度,即因子C,为高水平。工程师希望尽可能减少甲醛浓度,们一直未能做到这一点,因为这总
是造成渗透率太低

开始分析这些数据时,先将效应估计量画在正态概率纸上。24设计的对照常数的加号和减号表如表6.11所示。由这些对照,可以估计15个因子效应以及平方和,如表6.12所示。
这些效应的正态概率图如图611所示。沿直线上的所有效应可被忽路,而大的效应则远离此直线。此分析显露出的重要效应是主效应A,C,D以及AC交互作用和AD交互作用,


图6.12a画出了主效应A,C,D的图形。所有这3个效应都是正的,如果我们只考虑这些主效应,就可以将此3个效应以高水平来实验以使渗透率最大化。不过,还需考察任一重要的交互作用。我们知道,凡被显著的交互作用牵涉到的主效应,都没有多大的意义。
图6.12b画出了AC交互作用和AD交互作用的图形。这些交互作用是求解问题的关健。由AC交互作用看出,当浓度处于高水平时温度效应很小,当浓度处于低水平时温度效应很大,在低浓度,高温度时得到最好的结果。AD交互作用显示出,低祖时搅拌速度D的效应小,但高温时搅拌速度D有大的正的效应。因此,当A和D处于高水平而C处于低水平时,会得到最好的渗透率,这就允许将甲醛浓度减小至低水平,这是实验者的另一个目的


import numpy as np
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import pandas as pd
import statsmodels.api as sm
from sklearn import linear_model
import seaborn as sns
import matplotlib.pyplot as plt
import mistat
from scipy import special
from scipy.stats import ncx2
x1 = [-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1]
x2 = [-1,-1,1,1,-1,-1,1,1,-1,-1,1,1,-1,-1,1,1]
x3 = [-1,-1,-1,-1,1,1,1,1,-1,-1,-1,-1,1,1,1,1]
x4= [-1,-1,-1,-1,-1,-1,-1,-1,1,1,1,1,1,1,1,1]
y1 = [45,71,48,65,68,60,80,65,43,100,45,104,75,86,70,96]
data = {"y1":y1,"x1":x1,"x2":x2,"x3":x3,"x4":x4}
data=pd.DataFrame(data)
model1 = smf.ols(formula='data.y1 ~ data.x1*data.x2*data.x3*data.x4', data=data).fit()
print(model1.summary2())
#这个时候如果进行方差分析是得不到结果的
anova_table = sm.stats.anova_lm(model1, typ=2)
anova_table
#会出现如下错误提示:ValueError: array must not contain infs or NaNs
#下面改变模型
model1 = smf.ols(formula='data.y1 ~ data.x1+data.x2+data.x3+data.x4+data.x1*data.x2+data.x1*data.x3+data.x1*data.x4+data.x2*data.x3+data.x2*data.x4+data.x3*data.x4+data.x1*data.x2*data.x3+data.x1*data.x2*data.x4+data.x1*data.x3*data.x4+data.x2*data.x3*data.x4', data=data).fit()
print(model1.summary2())
anova_table = sm.stats.anova_lm(model1, typ=2)
anova_table
>>> anova_table
sum_sq df F PR(>F)
data.x1 1870.5625 1.0 247.347107 0.040424
data.x2 39.0625 1.0 5.165289 0.263883
data.x3 390.0625 1.0 51.578512 0.088077
data.x4 855.5625 1.0 113.132231 0.059678
data.x1:data.x2 0.0625 1.0 0.008264 0.942284
data.x1:data.x3 1314.0625 1.0 173.760331 0.048203
data.x1:data.x4 1105.5625 1.0 146.190083 0.052533
data.x2:data.x3 22.5625 1.0 2.983471 0.334095
data.x2:data.x4 0.5625 1.0 0.074380 0.830499
data.x3:data.x4 5.0625 1.0 0.669421 0.563451
data.x1:data.x2:data.x3 14.0625 1.0 1.859504 0.402820
data.x1:data.x2:data.x4 68.0625 1.0 9.000000 0.204833
data.x1:data.x3:data.x4 10.5625 1.0 1.396694 0.447071
data.x2:data.x3:data.x4 27.5625 1.0 3.644628 0.307178
Residual 7.5625 1.0 NaN NaN
1.设计投影
图6.11中的效应可以有另外的解释方式。因为B(压强)不显著且涉及B的所有交互作用可被忽略,所以可以在实验中放弃B使得设计变为A,C,D的有两次重复的23析因设计。考察表6.10中的列A,C,D,容易看出这些列形成有两次重复的23设计。使用这一简化假定,对数据进行的方差分析概括在表6.13中。由此分析所得的结论与由例6,2所得的结论本质上相同。注意,使用将24单次重复投影到有重复的23中去的方法,可以得到ACD交互作用的估计量以及建立在所谓的隐藏重复(hidden replication)基础上的误差估计量。

将无重复的析因设计投影到因子较少的有重复的析因设计中去这一概念非常有用。一般说来,如果有一个2k设计的单次重复,且其中的h(h<k)个因子可被忽略因而可被丢失,则原先的数据对应于留下来的k一h个因子的具有2h次重复的二水平析因设计。
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import pandas as pd
import statsmodels.api as sm
from sklearn import linear_model
import seaborn as sns
import matplotlib.pyplot as plt
import mistat
from scipy import special
from scipy.stats import ncx2
x1 = [-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1]
x2 = [-1,-1,1,1,-1,-1,1,1,-1,-1,1,1,-1,-1,1,1]
x3 = [-1,-1,-1,-1,1,1,1,1,-1,-1,-1,-1,1,1,1,1]
x4= [-1,-1,-1,-1,-1,-1,-1,-1,1,1,1,1,1,1,1,1]
y1 = [45,71,48,65,68,60,80,65,43,100,45,104,75,86,70,96]
data = {"y1":y1,"x1":x1,"x2":x2,"x3":x3,"x4":x4}
data=pd.DataFrame(data)
model1 = smf.ols(formula='data.y1 ~ data.x1+data.x3+data.x4+data.x1*data.x3+data.x1*data.x4+data.x3*data.x4+data.x1*data.x3*data.x4', data=data).fit()
print(model1.summary2())
anova_table = sm.stats.anova_lm(model1, typ=2)
anova_table
>>> anova_table
sum_sq df F PR(>F)
data.x1 1870.5625 1.0 83.367688 0.000017
data.x3 390.0625 1.0 17.384401 0.003124
data.x4 855.5625 1.0 38.130919 0.000267
data.x1:data.x3 1314.0625 1.0 58.565460 0.000060
data.x1:data.x4 1105.5625 1.0 49.272981 0.000110
data.x3:data.x4 5.0625 1.0 0.225627 0.647483
data.x1:data.x3:data.x4 10.5625 1.0 0.470752 0.512032
Residual 179.5000 8.0 NaN NaN
