当前位置：首页 > backend >正文

5 种距离算法总结！！

backend 2025/5/10 11:53:32

大家好！我是我不是小upper～

今天，咱们聚焦一个在机器学习领域极为关键、在实际项目中也高频使用的主题 ——距离算法。在机器学习的世界里，距离算法就像是一把 “度量尺”，专门用来衡量数据点之间的相似性或差异性。它的应用场景十分广泛，每一个场景都对算法的性能和效果起着至关重要的作用：

聚类分析：在聚类分析任务中，距离算法堪称核心工具。以 K 均值聚类为例，算法首先随机初始化 K 个聚类中心，随后通过不断计算每个数据点与这些聚类中心的距离，将数据点分配到距离最近的聚类簇中，并更新聚类中心的位置。这个迭代过程不断重复，直到聚类结果稳定。而层次聚类则是基于数据点之间的距离，通过计算簇与簇之间的距离，将距离近的簇逐步合并，构建出树形的聚类结构，最终根据需求确定合适的聚类层次。
最近邻分类：最近邻分类是一种直观且实用的基于距离的分类算法。其中，K 最近邻（KNN）算法的原理最为典型。当遇到一个待分类样本时，KNN 算法会计算该样本与训练集中所有样本的距离，然后找出距离最近的 K 个邻居样本。根据这 K 个邻居样本中出现频率最高的类别，来决定待分类样本的类别。例如，在手写数字识别任务中，通过计算待识别数字图像与训练集中图像的距离，找到最相似的 K 个数字图像，进而判断待识别数字的类别。
特征选择：在特征选择环节，距离算法能帮助我们评估特征之间的关联程度。我们可以通过计算特征向量之间的距离，来衡量特征之间的相关性或互信息。距离较近的特征，往往具有较高的相关性，可能存在信息冗余；而与目标变量距离较近的特征，则意味着它们与目标变量的关联更为紧密，对模型的贡献更大。通过筛选出与目标变量高度相关的特征，我们可以减少特征空间的维度，降低模型的复杂度，同时提升模型的性能和泛化能力。
异常检测：距离算法也是异常检测的重要手段。基于距离的异常检测方法，会将每个数据点与其邻近点之间的距离作为判断依据。当某个数据点与其他数据点的距离超出预先设定的阈值时，就会被认定为异常点或离群点。比如在银行交易数据中，如果某笔交易记录与其他正常交易记录的距离过大，就可能存在异常交易行为，需要进一步关注和审查。
降维：在处理高维数据集时，数据的复杂性和计算成本会显著增加。距离算法可以帮助我们在降低数据维度的同时，尽可能保留数据的重要结构信息。通过计算数据点之间的距离或相似性，我们可以将高维数据映射到一个较低维度的空间中。例如，主成分分析（PCA）就是一种常用的降维方法，它通过寻找数据的主要成分方向，将数据投影到这些方向上，从而实现降维。在这个过程中，距离算法用于衡量数据点在不同维度上的分布和差异，确保降维后的数据集能够最大程度地保留原始数据的特征和信息。

接下来，我将详细地去介绍5 种经典的距离算法，不仅会深入讲解算法的原理和适用场景，还会提供完整的 Python 代码，让大家能够轻松理解并应用这些算法到实际项目中！

欧几里德距离（Euclidean Distance）：

在度量空间中，欧几里德距离（Euclidean Distance）作为经典的距离度量方法，通过计算两点之间直线段的长度，精准刻画数据点间的空间差异，在数据挖掘、机器学习、图像处理等领域扮演着举足轻重的角色。

常见使用场景

数据挖掘领域：在海量数据处理中，欧几里德距离能够量化不同数据样本的相似程度。以聚类分析为例，算法依据数据点间的欧氏距离，将距离相近的样本聚为一类，从而挖掘数据内在的分布模式；在推荐系统中，通过计算用户行为数据或商品特征向量间的欧氏距离，找出相似用户或商品，实现精准推荐。
机器学习领域：在 K 近邻（KNN）等分类算法中，欧几里德距离是衡量特征相似性的核心工具。当新样本需要分类时，算法计算其与训练集中所有样本的欧氏距离，找出距离最近的 K 个邻居，依据邻居类别投票确定新样本归属，直观地将空间距离转化为分类决策依据。
图像处理领域：在图像匹配和检索任务中，欧几里德距离用于量化图像特征向量的差异。通过提取图像的颜色、纹理等特征，计算特征向量间的欧氏距离，距离越小则图像相似度越高，从而实现快速的图像检索与匹配。

下面是一个使用 Python 代码计算欧几里德距离：

import mathdef euclidean_distance(point1, point2):"""计算两个点之间的欧几里德距离输入参数：point1: 第一个点的坐标，格式为 (x1, y1)point2: 第二个点的坐标，格式为 (x2, y2)返回值：两个点之间的欧几里德距离"""x1, y1 = point1x2, y2 = point2distance = math.sqrt((x2 - x1)**2 + (y2 - y1)**2)return distance# 示例使用
point_1 = (2, 3)
point_2 = (5, 7)
distance = euclidean_distance(point_1, point_2)
print("两点之间的欧几里德距离：", distance)

上述代码定义了euclidean_distance函数，接收两个二维坐标点point1和point2作为参数。通过解包操作提取坐标值，依据欧几里德距离公式

$\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$ ，

利用math.sqrt函数计算并返回两点间的直线距离。以点(2, 3)和(5, 7)为例，经计算可得欧氏距离为5。

可视化演示

为了更直观地理解欧几里德距离，我们借助matplotlib库将两点及其距离可视化：

import matplotlib.pyplot as pltpoint1 = (2, 3)
point2 = (5, 7)# 计算欧几里德距离
distance = ((point2[0] - point1[0])**2 + (point2[1] - point1[1])**2)**0.5# 创建一个新的图形
fig, ax = plt.subplots()# 网格
ax.grid(True, linestyle='--', linewidth=0.5, color='gray')# 两个点
ax.plot(point1[0], point1[1], 'ro', label='A')
ax.plot(point2[0], point2[1], 'bo', label='B')# 连线
ax.plot([point1[0], point2[0]], [point1[1], point2[1]], 'k-', label='Distance')# 欧几里德距离标签
ax.annotate(f'Euclidean Distance: {distance:.2f}', xy=(3.5, 5), xytext=(3.5, 5))# 添加每个点的标签
ax.annotate('A', xy=point1, xytext=(point1[0]-0.8, point1[1]+0.3))
ax.annotate('B', xy=point2, xytext=(point2[0]-0.8, point2[1]+0.3))
ax.annotate(f'{distance:.2f}', xy=((point1[0]+point2[0])/2, (point1[1]+point2[1])/2),xytext=((point1[0]+point2[0])/2-0.5, (point1[1]+point2[1])/2+0.4))# 设置坐标轴范围
ax.set_xlim(0, 6)
ax.set_ylim(0, 8)# 添加图例
ax.legend()plt.show()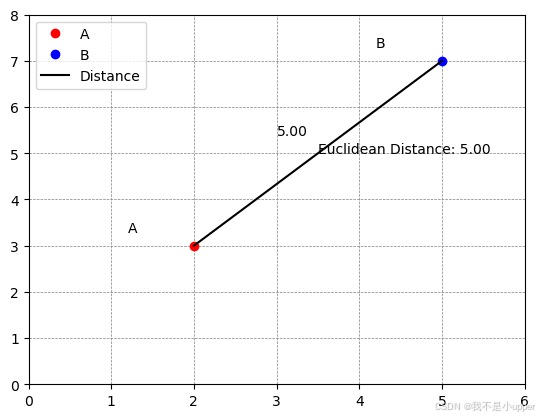

运行代码后，将生成一个带有灰色网格的二维坐标系。其中，红点A代表坐标(2, 3)，蓝点B代表坐标(5, 7)，黑色线段连接两点直观呈现欧几里德距离。图中还添加了清晰的标注，包括点的标签、距离数值标签，以及图例说明，可以帮助我们更直观地理解欧氏距离在二维空间中的几何意义。

曼哈顿距离（Manhattan Distance）：

曼哈顿距离，又被称作城市街区距离或 L1 距离，是一种独特的距离度量方式。它与欧几里德距离直接计算两点间直线长度不同，曼哈顿距离更像是在城市网格状的街区中，从一个地点到另一个地点沿着街道横竖行走的总路程，通过计算两点在各个坐标轴上差值的绝对值之和，来衡量它们之间的距离。

常见使用场景

路径规划：在网格地图场景中，如城市道路规划、游戏地图导航等，曼哈顿距离是计算最短路径的得力助手。由于现实中的道路往往呈网格状布局，两点间无法直接直线通行，而曼哈顿距离恰好能模拟行人或车辆在街道上横向、纵向移动的实际路程，帮助规划出符合实际道路规则的最短路线。
物流管理：在物流配送环节，仓库与各个配送目的地通常分布在城市的不同区域，道路网络也多为网格状。曼哈顿距离可以精准计算货物从仓库到目的地的最短配送路径，考虑到实际交通规则和道路布局，为物流调度提供合理的参考，优化配送路线，减少运输成本和时间。
特征选择：在数据分析与机器学习领域，曼哈顿距离可用于评估特征之间的相关性。通过计算不同特征向量在各个维度上的差异绝对值之和，来衡量特征之间的相似程度或关联程度。以此为依据，能够筛选出与目标变量相关性高的特征，剔除冗余或无关特征，实现特征选择和降维，提高模型的效率和性能。

下面使用Python代码计算曼哈顿距离：

def manhattan_distance(point1, point2):"""计算两个点之间的曼哈顿距离输入参数：point1: 第一个点的坐标，格式为 (x1, y1)point2: 第二个点的坐标，格式为 (x2, y2)返回值：两个点之间的曼哈顿距离"""x1, y1 = point1x2, y2 = point2distance = abs(x2 - x1) + abs(y2 - y1)return distance# 示例使用
point_1 = (2, 3)
point_2 = (5, 7)
distance = manhattan_distance(point_1, point_2)
print("两点之间的曼哈顿距离：", distance)

对于示例中的点（2, 3）和（5, 7），计算结果为下图：

网上特别流行的一张图：

该图形展示了二维平面上两个点A和B之间的曼哈顿距离。曼哈顿距离是通过在坐标轴上的横向和纵向移动来测量的，即将水平方向和垂直方向的距离相加。

切比雪夫距离（Chebyshev Distance）：

在度量空间中，切比雪夫距离是一种独特且实用的距离度量方式，专门用于刻画两个向量之间的差异程度。它的核心定义为：两个向量在各个维度上元素差值的最大值，这个 “最大差值” 就代表了两个向量间的切比雪夫距离。从数学公式来看，若有两个向量 $\mathbf{x}=(x_1,x_2,\cdots,x_n)$ 和 $\mathbf{y}=(y_1,y_2,\cdots,y_n)$ ，它们之间的切比雪夫距离 $d(\mathbf{x},\mathbf{y})$ 表示为：

$d(\mathbf{x},\mathbf{y}) = \max_{i=1}^{n} \vert x_i - y_i \vert$

其中，n为向量的维度， $\vert x_i - y_i \vert$ 计算的是两个向量在第i个维度上元素的差值绝对值，而整个公式就是在所有维度的差值绝对值中取最大值。

常见使用场景

图像处理领域：在图像分类、对象识别和图像匹配等任务中，切比雪夫距离发挥着重要作用。例如，在对图像特征进行分析时，可将图像的某些特征抽象为向量，通过计算不同图像特征向量间的切比雪夫距离，判断图像的相似性。若两张图像特征向量在某一关键维度上差异过大（即切比雪夫距离的那个 “最大差值” 过大），则说明这两张图像在该特征上有明显区别，有助于快速筛选出符合特定条件的图像。
机器学习领域：在聚类算法，如 K - means 算法中，切比雪夫距离可作为衡量数据点间相似性的度量标准。传统 K - means 算法常用欧几里得距离，但在某些场景下，数据点在某些维度上的差异对聚类结果影响更大，此时使用切比雪夫距离，以 “最大维度差距” 来划分数据点，能更好地反映数据间的内在结构，得到更符合需求的聚类结果。
异常检测领域：切比雪夫距离常用于识别异常数据点。在一组数据中，每个数据可看作高维空间中的一个向量，当某个数据向量与其他正常数据向量在某一维度上的差异显著超出正常范围（即与其他向量的切比雪夫距离过大），就可将其判定为异常数据，帮助人们及时发现数据集中的异常情况，以便进一步分析处理。

下面使用 Python 计算切比雪夫距离：

def chebyshev_distance(x, y):assert len(x) == len(y), "Vectors must have the same length"return max(abs(a - b) for a, b in zip(x, y))# 例子：计算两个向量的切比雪夫距离
vector1 = [1, 2, 3]
vector2 = [4, 5, 6]
distance = chebyshev_distance(vector1, vector2)
print("切比雪夫距离:", distance)

上述代码定义了chebyshev_distance函数，专门用于计算两个向量之间的切比雪夫距离。函数接收两个向量参数x和y，首先通过assert len(x) == len(y)语句进行条件判断，确保输入的两个向量长度一致。因为只有维度相同的向量，计算它们在各维度上的差值才有意义，若向量长度不同，就无法准确计算切比雪夫距离，此时程序会抛出异常提示 “Vectors must have the same length”。

在确认向量长度一致后，函数使用了一个精妙的生成器表达式abs(a - b) for a, b in zip(x, y)。这里的zip(x, y)函数将两个向量x和y中对应位置的元素一一配对，例如x的第一个元素与y的第一个元素组成一对，第二个元素与第二个元素组成一对，以此类推。然后，abs(a - b)计算每一对元素的差值绝对值，最后通过max()函数从所有这些差值绝对值中找出最大值，这个最大值就是两个向量之间的切比雪夫距离，并将其返回。

以向量vector1 = [1, 2, 3]和vector2 = [4, 5, 6]为例，它们对应元素的差值绝对值分别为abs(1 - 4)=3、abs(2 - 5)=3、abs(3 - 6)=3，通过max()函数选取最大值，最终得到切比雪夫距离为3，程序输出 “切比雪夫距离: 3” 。

闵可夫斯基距离（Minkowski Distance）：

在向量空间的度量体系中，闵可夫斯基距离堪称一座 “桥梁”，它将多种经典距离度量方法统一在一个公式框架之下，是切比雪夫距离、欧几里得距离和曼哈顿距离的通用化表达。通过调整关键参数，闵可夫斯基距离能够灵活切换，适配不同场景下的距离计算需求。

从数学定义来看，对于两个向量 $\mathbf{x}=(x_1,x_2,\cdots,x_n)$ 和 $\mathbf{y}=(y_1,y_2,\cdots,y_n)$ ，闵可夫斯基距离 $d(\mathbf{x},\mathbf{y})$ 的计算公式为：

$d(\mathbf{x},\mathbf{y}) = \left(\sum_{i = 1}^{n} \vert x_i - y_i \vert^p\right)^{\frac{1}{p}}$

其中，n 表示向量的维度， $\vert x_i - y_i \vert$ 计算的是两个向量在第 i 个维度上元素的差值绝对值，p 是一个大于 0 的实数参数，它决定了距离度量的特性和类型。

特殊情况解析

当 p = 1 时：闵可夫斯基距离退化为曼哈顿距离（Manhattan Distance），也被称为城市街区距离或 L1 距离。此时的计算公式变为： $d(\mathbf{x},\mathbf{y}) = \sum_{i = 1}^{n} \vert x_i - y_i \vert$ 在二维平面中，若向量 A 的坐标为 $(x_1, y_1)$ ，向量 B 的坐标为 ( $x_2, y_2$ )，则曼哈顿距离表示从点 A 到点 B 在网格状路径（只能沿水平或垂直方向移动）上的最短行走距离，就像在城市街区中从一个路口到另一个路口的路程计算方式。
当 p = 2 时：闵可夫斯基距离转化为欧几里得距离（Euclidean Distance），是最直观的直线距离度量。计算公式如下： $d(\mathbf{x},\mathbf{y}) = \sqrt{\sum_{i = 1}^{n} (x_i - y_i)^2}$ 在二维空间中，它代表两点之间直线段的长度；在高维向量空间里，同样用于计算两点间的 “直线” 距离，广泛应用于几何学、机器学习等领域。
当 $p \to +\infty$ 时：闵可夫斯基距离趋近于切比雪夫距离（Chebyshev Distance），其本质是取两个向量在各个维度上元素差的最大值，即： $d(\mathbf{x},\mathbf{y}) = \max_{i = 1}^{n} \vert x_i - y_i \vert$

由此可见，参数 p 就像一个 “调控开关”，改变 p 的取值，就能调整距离计算中各个维度的权重分布，实现从不同角度衡量向量间的差异。

常见使用场景

数据挖掘领域：在聚类、分类和异常检测等任务中，闵可夫斯基距离为数据间的相似性度量提供了灵活的选择。例如，在聚类分析时，通过调整 p 值，可以根据数据特点选择合适的距离度量方式，使聚类结果更贴合数据内在结构；在异常检测中，也能通过它精准识别与其他数据点差异较大的异常点。
图像处理领域：在图像匹配、对象识别和图像检索等场景中，闵可夫斯基距离可用于量化图像特征向量之间的差异。比如，将图像的颜色、纹理等特征转换为向量后，根据不同的任务需求选择合适的 p 值计算距离，从而快速找到相似图像。
文本挖掘领域：在文本分类、信息检索和自然语言处理等任务里，闵可夫斯基距离能够度量文本向量之间的相似度。将文本表示为向量形式后，利用它可以计算不同文本间的距离，进而实现文本分类、检索相关文档等功能。

下面使用 Python 计算闵可夫斯基距离：

import mathdef minkowski_distance(x, y, p):assert len(x) == len(y), "Vectors must have the same length"return math.pow(sum(math.pow(abs(a - b), p) for a, b in zip(x, y)), 1/p)# 例子：计算两个向量的闵可夫斯基距离
vector1 = [1, 2, 3]
vector2 = [4, 5, 6]
distance = minkowski_distance(vector1, vector2, 3)
print("闵可夫斯基距离:", distance)

上述代码定义了 minkowski_distance 函数，专门用于计算两个向量之间的闵可夫斯基距离。函数接收三个参数：向量 x、向量 y 以及参数 p。首先，通过 assert len(x) == len(y) 语句确保输入的两个向量长度一致，因为只有维度相同的向量，才能依据公式准确计算闵可夫斯基距离，若长度不同，程序会抛出异常提示 “Vectors must have the same length”。

接下来，函数使用了一个嵌套的生成器表达式 math.pow(abs(a - b), p) for a, b in zip(x, y)。其中，zip(x, y) 将两个向量中对应位置的元素一一配对，abs(a - b) 计算每一对元素的差值绝对值，math.pow(abs(a - b), p) 对差值绝对值进行 p 次幂运算。sum() 函数将所有维度上计算得到的 p 次幂结果求和，最后通过 math.pow(..., 1/p) 对求和结果进行 $\frac{1}{p}$ 次幂运算，也就是开 p 次方，得到的最终结果就是两个向量之间的闵可夫斯基距离，并将其返回。

以向量 vector1 = [1, 2, 3] 和 vector2 = [4, 5, 6] 为例，当 p = 3 时，经过函数的一系列计算，最终得到闵可夫斯基距离为 4.326748710922225，程序输出 “闵可夫斯基距离: 4.326748710922225” 。

余弦相似度（Cosine Similarity）：

在机器学习和数据挖掘领域，余弦相似度是一种应用极为广泛的相似性度量方法，它专注于衡量两个向量在方向上的相似程度，通过计算两个向量夹角的余弦值，巧妙地揭示数据之间的内在关联。与传统距离度量方法（如欧几里得距离）不同，余弦相似度更关注向量的方向一致性，而非向量的长度差异，这使得它在处理高维数据时展现出独特的优势。

核心公式解析

余弦相似度的计算公式如下：

$\text{Cosine Similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|} = \frac{\sum_{i = 1}^{n} A_i B_i}{\sqrt{\sum_{i = 1}^{n} A_i^2} \sqrt{\sum_{i = 1}^{n} B_i^2}}$

其中， $\mathbf{A}=(A_1,A_2,\cdots,A_n)$ 和 $\mathbf{B}=(B_1,B_2,\cdots,B_n)$ 是待比较的两个向量； $\mathbf{A} \cdot \mathbf{B}$ 表示向量 $\mathbf{A}$ 和 $\mathbf{B}$ 的点积，它等于对应元素乘积的总和； $\|\mathbf{A}\|$ 和 $\|\mathbf{B}\|$ 分别是向量 $\mathbf{A}$ 和 $\mathbf{B}$ 的模（长度），通过对各元素平方和开方计算得到。从几何角度来看，该公式计算的就是两个向量夹角的余弦值，余弦值越接近 1，说明两个向量的方向越相近，数据的相似性越高；余弦值越接近 -1，则表示两个向量方向相反；当余弦值为 0 时，意味着两个向量相互垂直，即数据之间不存在相似性。

常见使用场景

文本相似度计算：在自然语言处理领域，文本通常被转化为高维向量（如词向量、TF-IDF 向量）进行表示。余弦相似度可以高效地计算不同文本向量之间的相似程度，广泛应用于文本分类、信息检索、文本查重等任务。例如，在搜索引擎中，通过计算用户查询文本与文档库中文档的余弦相似度，能够快速筛选出与查询内容最相关的文档；在文本分类任务中，根据待分类文本与各类别样本的余弦相似度，判断其所属类别。
推荐系统：推荐系统中，用户和商品的特征往往被抽象为向量形式。通过计算用户特征向量与商品特征向量的余弦相似度，可以找到与用户兴趣最匹配的商品，为用户提供个性化推荐。比如，电商平台根据用户的历史购买记录、浏览行为等生成用户特征向量，同时将商品的属性、类别等信息转化为商品特征向量，利用余弦相似度计算两者的相似性，进而向用户推荐相似性较高的商品。
图像处理：在图像处理任务中，图像的特征（如颜色直方图、局部特征描述子等）可以用向量表示。余弦相似度用于衡量不同图像向量之间的相似性，在图像匹配、图像检索、图像聚类等方面发挥重要作用。例如，在图片搜索应用中，用户上传一张图片，系统将其特征向量与数据库中图片的特征向量进行余弦相似度计算，返回相似性高的图片作为搜索结果。

对于直观理解余弦相似度的计算过程，我们用Python代码再来表示：

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity# 定义两个向量 A 和 B
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])# 将向量转换为行向量
A = A.reshape(1, -1)
B = B.reshape(1, -1)# 计算余弦相似度
similarity = cosine_similarity(A, B)[0][0]print("余弦相似度:", similarity)

上述代码借助 numpy 库和 sklearn 库中的 cosine_similarity 函数，实现了余弦相似度的快速计算。首先，使用 np.array 定义了两个向量 A 和 B。由于 cosine_similarity 函数期望输入的是二维数组（每一行代表一个向量），因此通过 reshape(1, -1) 将一维向量转换为只有一行的二维行向量。最后，调用 cosine_similarity 函数传入两个行向量，函数返回一个二维数组，其中 [0][0] 表示第一个向量（即 A）与第二个向量（即 B）之间的余弦相似度，将结果打印输出。

可视化理解

为了更直观地理解余弦相似度的计算原理，我们通过以下代码进行可视化展示：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Arc# 定义两个向量 A 和 B
A = np.array([1, 2])
B = np.array([2, 3])# 计算向量 A 和 B 的模
norm_a = np.linalg.norm(A)
norm_b = np.linalg.norm(B)# 计算夹角余弦值
cos_theta = np.dot(A, B) / (norm_a * norm_b)# 绘制向量 A 和 B
plt.quiver(0, 0, A[0], A[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.quiver(0, 0, B[0], B[1], angles='xy', scale_units='xy', scale=1, color='b')# 绘制夹角
theta = np.arccos(cos_theta)
arc = Arc((0,0), 0.5, 0.5, angle=0, theta1=0, theta2=np.degrees(theta))
plt.gca().add_patch(arc)# 设置坐标轴范围
plt.xlim(-1, 3)
plt.ylim(-1, 4)# 添加标签和标题
plt.text(1, 2.5, 'A', fontsize=12)
plt.text(2, 3.5, 'B', fontsize=12)
plt.title('Cosine Similarity')# 显示图形
plt.grid()
plt.show()

这段代码使用 matplotlib 库绘制了二维平面上的两个向量 A 和 B，并直观呈现了它们之间的夹角。首先，定义向量 A 和 B 后，通过 np.linalg.norm 函数计算向量的模，利用 np.dot 函数计算点积，进而得到夹角的余弦值 cos_theta。接着，使用 plt.quiver 函数以箭头形式绘制出向量 A 和 B，箭头起点为坐标原点 (0, 0)，箭头方向和长度对应向量的方向和模。然后，通过 np.arccos 函数将余弦值转换为弧度制的夹角 theta，使用 Arc 类绘制表示夹角的圆弧，并添加到图形中。最后，设置坐标轴范围、添加向量标签和图形标题，并通过 plt.show() 显示可视化图形，帮助我们更清晰地理解余弦相似度与向量夹角之间的关系。