基础RNN网络详解
循环神经网络(Recurrent Neural Network, RNN)是一类专门用于处理序列数据的神经网络架构。与传统的前馈神经网络不同,RNN引入了"记忆"的概念,能够利用之前的信息来处理当前的输入。
1. RNN的基本结构
RNN的核心思想是将网络的隐藏状态在时间步之间传递,使网络具有记忆能力。其基本结构可以表示为:

x:当前时间步的输入
h:隐藏状态(传递记忆信息)
y:当前时间步的输出
箭头方向:数据流动方向(h的循环箭头表示状态传递)
数学表示
对于一个时间步t:
- 输入:xₜ
- 隐藏状态:hₜ = f(Wₕₕ·hₜ₋₁ + Wₓₕ·xₜ + bₕ)
- 输出:yₜ = g(Wₕᵧ·hₜ + bᵧ)
其中:
- Wₕₕ:隐藏层到隐藏层的权重矩阵
- Wₓₕ:输入到隐藏层的权重矩阵
- Wₕᵧ:隐藏层到输出层的权重矩阵
- bₕ, bᵧ:偏置项
- f, g:激活函数(通常f使用tanh或ReLU,g根据任务选择)
2. RNN的展开形式
为了更清楚地理解RNN如何处理序列数据,我们可以将其在时间维度上展开:
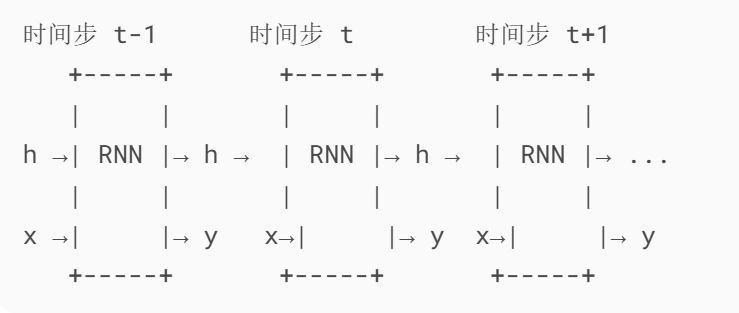
关键特点:
每个时间步共享同一组参数(W_xh, W_hh, W_hy)
隐藏状态h像"记忆"一样在时间步间传递
输出y可选择性使用(如只在最后时间步输出)
这种展开形式显示了RNN如何在每个时间步处理输入并传递隐藏状态。
3. RNN的常见类型
根据输入和输出的关系,RNN可以分为几种类型:
- 一对一:传统的前馈神经网络结构
- 一对多:如图像字幕生成(单张图像→单词序列)
- 多对一:如情感分析(单词序列→情感)
- 多对多(等长):如视频帧分类(每帧对应一个标签)
- 多对多(不等长):如机器翻译(不同长度的输入输出序列)
4. RNN的训练:BPTT算法
RNN使用随时间反向传播(Backpropagation Through Time, BPTT)算法进行训练:
- 前向传播整个序列,计算每个时间步的输出
- 计算每个时间步的损失(通常使用交叉熵或均方误差)
- 反向传播误差,计算梯度
- 更新权重参数
梯度消失与爆炸问题
RNN在训练长序列时面临的主要挑战:
- 梯度消失:梯度随着时间步呈指数衰减,较早时间步的信息难以影响参数更新
- 梯度爆炸:梯度随着时间步呈指数增长,导致训练不稳定
解决方案:
- 梯度裁剪(针对梯度爆炸)
- 使用LSTM或GRU等改进结构
- 使用残差连接
5. RNN的局限性
尽管RNN是处理序列数据的基础模型,但它有一些明显的局限性:
- 难以捕获长期依赖关系(由于梯度消失问题)
- 计算是顺序的,难以并行化
- 对长序列的记忆能力有限
这些局限性导致了更先进的架构如LSTM和GRU的发展,以及后来Transformer架构的出现。
6. 简单RNN的Python实现示例
import numpy as npclass SimpleRNN:def __init__(self, input_size, hidden_size, output_size):# 权重初始化self.Wxh = np.random.randn(hidden_size, input_size) * 0.01self.Whh = np.random.randn(hidden_size, hidden_size) * 0.01self.Why = np.random.randn(output_size, hidden_size) * 0.01# 偏置初始化self.bh = np.zeros((hidden_size, 1))self.by = np.zeros((output_size, 1))def forward(self, inputs):# 初始化隐藏状态h = np.zeros((self.Whh.shape[0], 1))self.last_inputs = inputsself.last_hs = { -1: h }# 前向传播for i, x in enumerate(inputs):h = np.tanh(np.dot(self.Wxh, x) + np.dot(self.Whh, h) + self.bh)self.last_hs[i] = h# 计算输出y = np.dot(self.Why, h) + self.byreturn y, hdef backward(self, d_y, learn_rate=0.01):# 初始化梯度d_Wxh = np.zeros_like(self.Wxh)d_Whh = np.zeros_like(self.Whh)d_Why = np.zeros_like(self.Why)d_bh = np.zeros_like(self.bh)d_by = np.zeros_like(self.by)d_h_next = np.zeros_like(self.last_hs[0])# 反向传播for t in reversed(range(len(self.last_inputs))):h = self.last_hs[t]h_prev = self.last_hs[t-1]# 输出层的梯度d_Why += np.dot(d_y, h.T)d_by += d_y# 隐藏层的梯度d_h = np.dot(self.Why.T, d_y) + d_h_nextd_h_raw = (1 - h * h) * d_h # tanh的导数d_bh += d_h_rawd_Wxh += np.dot(d_h_raw, self.last_inputs[t].T)d_Whh += np.dot(d_h_raw, h_prev.T)d_h_next = np.dot(self.Whh.T, d_h_raw)# 裁剪梯度防止爆炸for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:np.clip(d, -1, 1, out=d)# 更新参数self.Wxh -= learn_rate * d_Wxhself.Whh -= learn_rate * d_Whhself.Why -= learn_rate * d_Whyself.bh -= learn_rate * d_bhself.by -= learn_rate * d_by
7. RNN的应用场景
尽管有更先进的架构,基础RNN仍然在一些场景中有应用价值:
- 简单的时间序列预测
- 字符级语言模型
- 低资源环境下的序列处理任务
- 教学和理解序列模型的基础
总结
基础RNN是理解更复杂序列模型的重要起点。虽然它有一些局限性,但其核心思想——在时间步之间保持和传递隐藏状态——仍然是许多现代序列模型的基础。理解RNN的工作原理有助于更好地掌握LSTM、GRU以及Transformer等更先进的架构。
