序列容器(vector,deque,list)
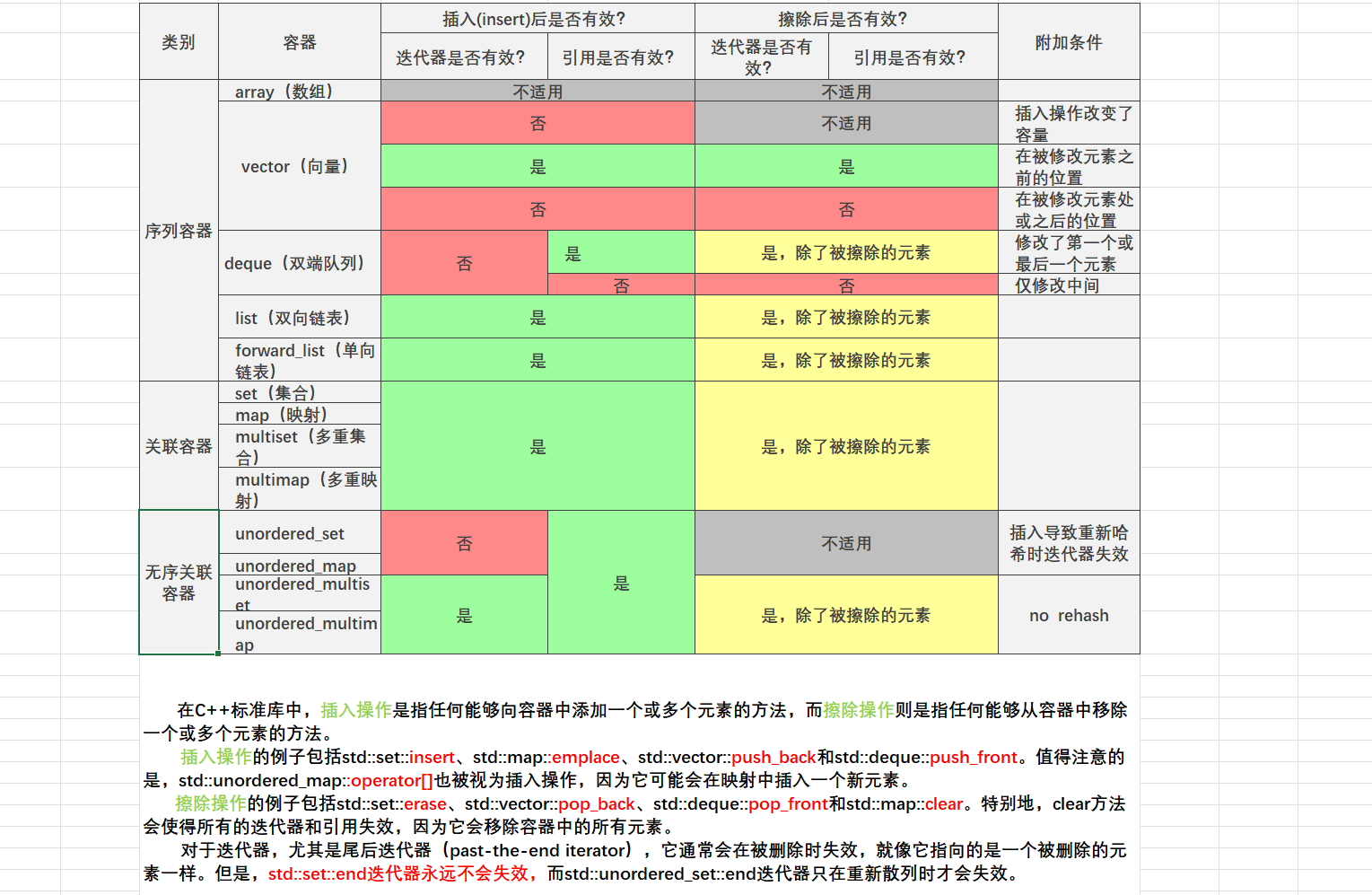
STL 序列式容器(vector、deque、list、array、forward_list)的核心特征是按插入顺序存储元素(元素的逻辑顺序与物理存储顺序一致)
vector
下图是底层原理 具体点击链接vector介绍
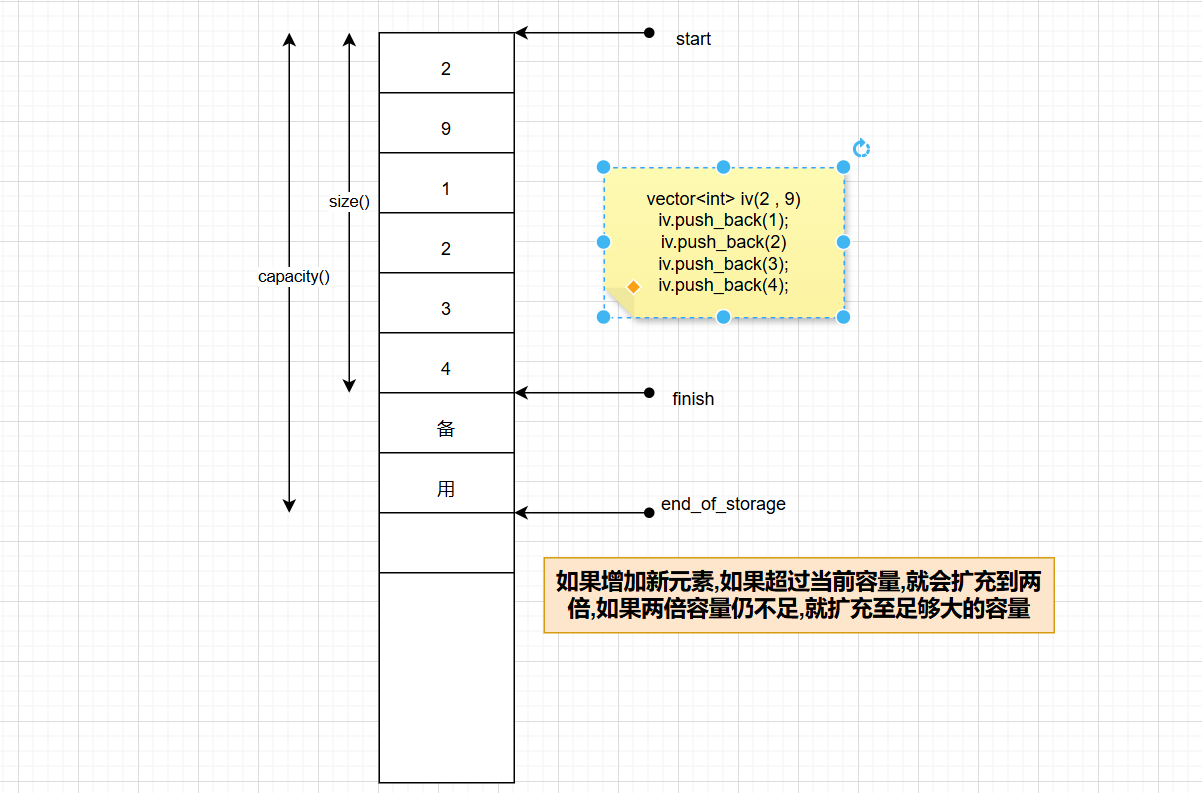
deque(双端队列)
在 C++ STL 中,deque(Double-Ended Queue,双端队列)是一种支持两端高效插入 / 删除的序列式容器,底层通过 “分段动态数组 + 中控数组” 的结构实现,兼顾了随机访问能力和双端操作效率。以下从核心特性、底层原理、常用接口、适用场景等方面全面解析 deque:
一、核心特性
-
双端高效操作
- 头部(
front)和尾部(back)的插入(push_front/push_back)、删除(pop_front/pop_back)操作均为 O (1) 时间复杂度(无需像vector那样移动大量元素,也无需像list那样分配节点)。
- 头部(
-
支持随机访问
- 提供下标运算符(
[])和at()成员函数,可直接访问指定位置的元素,时间复杂度 O(1)(优于list的 O (n),但底层实现比vector复杂)。
- 提供下标运算符(
-
动态扩容
- 容量不足时会自动扩容,但扩容逻辑比
vector更灵活:vector扩容需分配新的连续内存并拷贝所有元素(O (n) 开销),而deque只需新增一个 “分段数组” 并更新中控数组(避免大规模拷贝,平均扩容开销更低)。
- 容量不足时会自动扩容,但扩容逻辑比
-
非连续内存存储
- 底层并非连续内存(与
vector不同),而是由多个小型连续内存块(分段数组)和一个 “中控数组”(存储各分段数组的地址)组成,通过中控数组实现对分段的管理,对外表现为 “连续的元素序列”。
- 底层并非连续内存(与
二、底层原理(为什么能兼顾双端操作和随机访问?)
deque 的底层结构可拆解为两部分,理解这部分能更清晰其特性来源:
-
分段数组(Buffer)
- 每个分段数组是固定大小的连续内存块(例如默认 512 字节),用于存储实际的元素;
- 分段数组的大小可通过编译器宏(如
_DEQUE_BUF_SIZE)调整,也可在定义deque时通过模板参数指定。
-
中控数组(Map)
- 本质是一个 “指针数组”,每个元素指向一个分段数组;
- 中控数组会预留一定的空闲位置(头部和尾部),当头部需要插入元素且当前首分段已满时,直接在中控数组头部新增一个分段指针;尾部同理,避免中控数组频繁扩容。
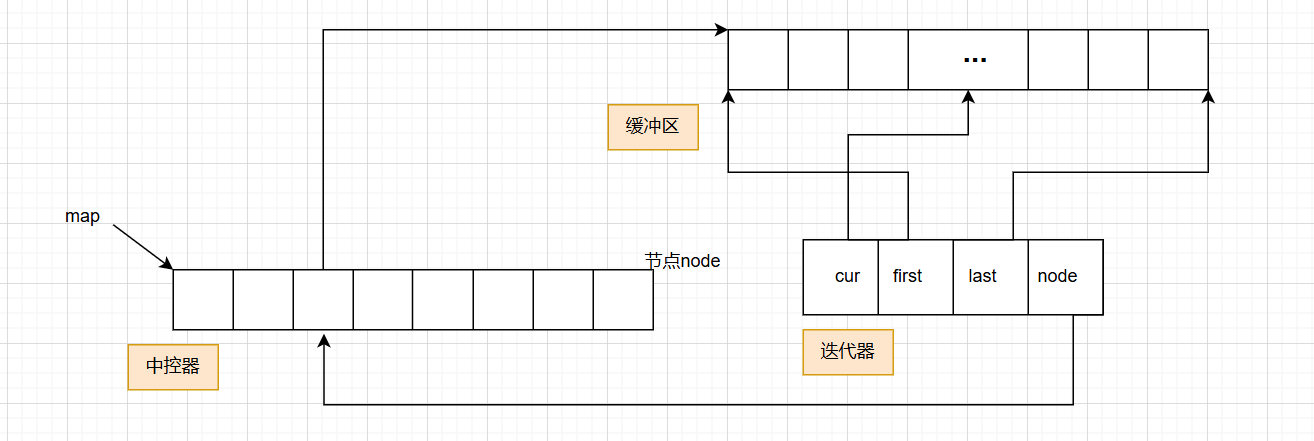
访问元素的逻辑:
当通过下标 i 访问 deque 元素时,底层会先计算 i 所在的 “分段索引”(i / 分段大小)和 “分段内偏移”(i % 分段大小),再通过中控数组找到对应的分段数组,最后通过偏移获取元素 —— 这一过程是 O (1),因此支持随机访问。
三、常用成员函数(核心接口)
deque 的接口与 vector 类似,但新增了双端操作的接口,以下是高频使用的成员函数:
| 类别 | 成员函数 | 功能描述 |
|---|---|---|
| 构造 / 析构 | deque() | 默认构造空的 deque |
deque(n, val) | 构造包含 n 个 val 的 deque | |
deque(beg, end) | 从迭代器范围 [beg, end) 构造 deque(如从 vector 或 string 初始化) | |
| 双端操作 | push_front(val) | 在头部插入元素 val(O(1)) |
push_back(val) | 在尾部插入元素 val(O(1)) | |
pop_front() | 删除头部元素(O (1),需确保 deque 非空) | |
pop_back() | 删除尾部元素(O (1),需确保 deque 非空) | |
| 元素访问 | operator[](i) | 访问下标 i 处的元素(无越界检查,越界行为未定义) |
at(i) | 访问下标 i 处的元素(有越界检查,越界抛 out_of_range 异常) | |
front() | 获取头部元素(O (1)) | |
back() | 获取尾部元素(O (1)) | |
| 容量操作 | size() | 返回元素个数(O (1)) |
empty() | 判断是否为空(O (1),空返回 true) | |
resize(n, val) | 调整元素个数为 n:不足补 val,多余删除 | |
clear() | 清空所有元素(O (n),元素析构,但中控数组和分段数组可能保留以复用) | |
| 迭代器 | begin()/end() | 获取首元素 / 尾后元素的迭代器(支持随机访问,可 ++/--/+n/-n) |
rbegin()/rend() | 获取反向迭代器(从尾部向头部遍历) |
四、适用场景(什么时候用 deque?)
deque 的特性决定了它适合 “需要双端操作 + 随机访问” 的场景,典型场景包括:
-
实现队列(Queue)或双端队列
- STL 的
queue容器适配器默认以deque为底层容器(因为queue需支持push_back和pop_front,deque这两个操作都是 O (1),优于vector的pop_front(O(n)))。
- STL 的
-
频繁在两端插入 / 删除,且需要随机访问
- 例如:滑动窗口算法(需在窗口两端添加 / 移除元素,同时访问窗口内任意位置元素)、日志存储(新日志追加到尾部,旧日志从头部删除,偶尔需查询中间日志)。
-
替代
vector避免大规模扩容开销- 当
vector存储大量元素时,扩容会拷贝所有元素,开销较大;而deque扩容只需新增分段,适合元素数量动态增长且规模较大的场景(但随机访问效率略低于vector,需权衡)。
- 当
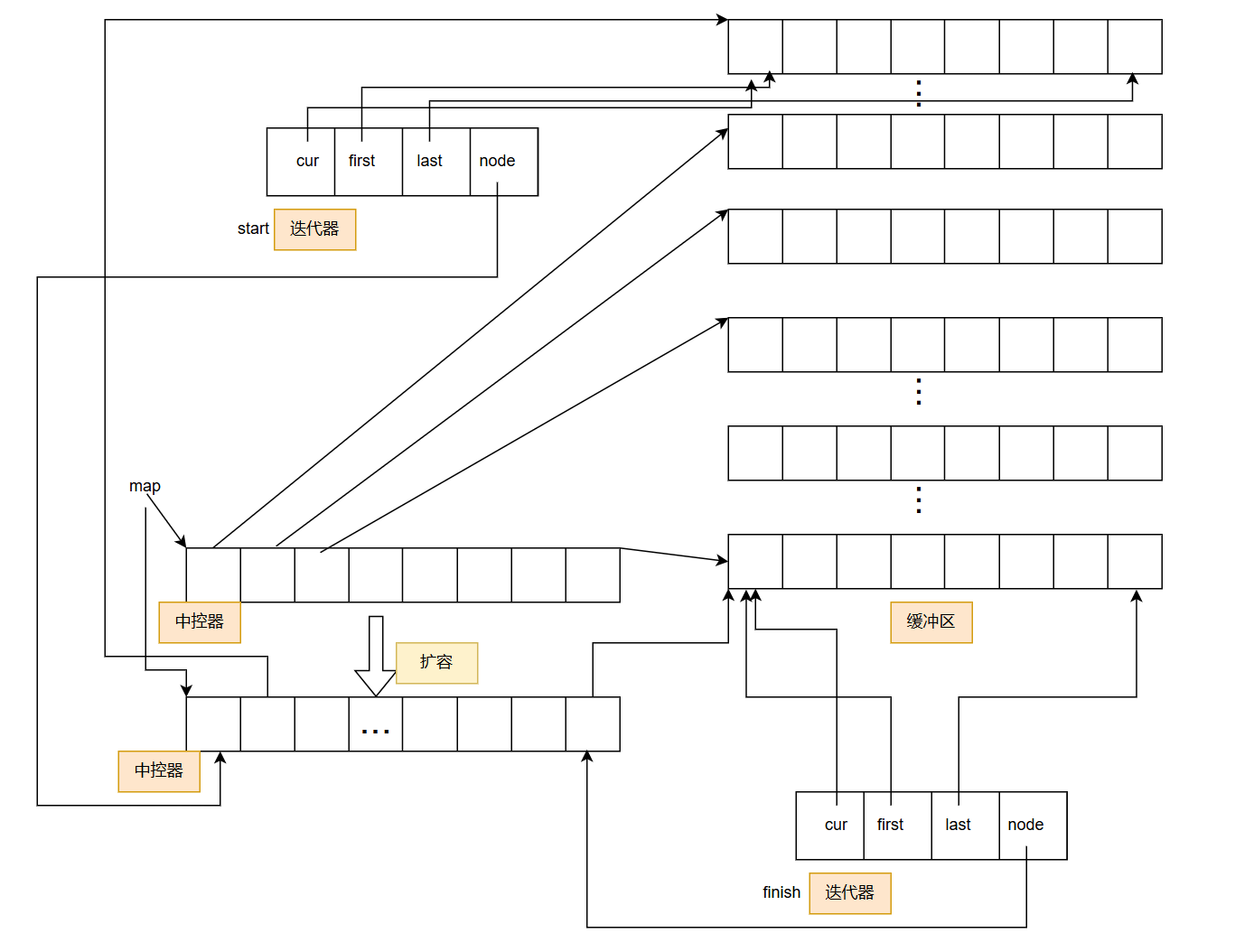
五、与其他容器的对比(vector vs list vs deque)
| 特性 | vector | list | deque |
|---|---|---|---|
| 底层结构 | 连续动态数组 | 双向链表 | 分段数组 + 中控数组 |
随机访问([]/at) | 支持(O (1)) | 不支持(O (n)) | 支持(O (1)) |
| 头部插入 / 删除 | 不支持头部插入,可以删除 | 高效(O (1)) | 高效(O (1)) |
| 尾部插入 / 删除 | 高效(O (1),扩容时 O (n)) | 高效(O (1)) | 高效(O (1)) |
| 中间插入 / 删除 | 不高效(O (n)) | 高效(O (1),找位置 O (n)) | 不高效(O (n)) |
| 内存利用率 | 高(连续内存,缓存友好) | 低(节点有指针开销) | 中等(分段有少量浪费) |
| 扩容开销 | 高(拷贝所有元素) | 低(仅分配新节点) | 低(新增分段) |
六、使用示例(代码演示)
#include <iostream>
#include <deque>
#include <algorithm> // 用于 sort 等算法int main() {// 1. 构造 deque 并初始化std::deque<int> dq1; // 空 dequestd::deque<int> dq2(5, 10); // 5个10:[10,10,10,10,10]std::deque<int> dq3(dq2.begin(), dq2.end()); // 从 dq2 复制:[10,10,10,10,10]// 2. 双端插入元素dq1.push_back(20); // 尾部插入:[20]dq1.push_front(10); // 头部插入:[10,20]dq1.push_back(30); // 尾部插入:[10,20,30]// 3. 随机访问和遍历std::cout << "dq1[1] = " << dq1[1] << std::endl; // 输出 20(随机访问)std::cout << "dq1 遍历:";for (int i = 0; i < dq1.size(); ++i) {std::cout << dq1[i] << " "; // 10 20 30}std::cout << std::endl;// 4. 双端删除元素dq1.pop_front(); // 删除头部:[20,30]dq1.pop_back(); // 删除尾部:[20]// 5. 排序(支持随机访问迭代器,可直接用 sort 算法)std::deque<int> dq4 = {3, 1, 4, 2};std::sort(dq4.begin(), dq4.end()); // 排序后:[1,2,3,4]std::cout << "排序后 dq4:";for (auto val : dq4) {std::cout << val << " "; // 1 2 3 4}return 0;
}
七、注意事项
- 避免中间插入 / 删除:
deque中间插入 / 删除需要移动该位置两侧的元素(O (n) 时间),效率低,若需频繁中间操作,优先用list。 - 迭代器稳定性:
deque的迭代器在扩容时可能失效(中控数组扩容会导致分段指针地址变化),但在两端插入 / 删除时,除了首分段和尾分段的迭代器,其他分段的迭代器仍有效(与vector所有迭代器失效不同)。 - 不适合存储大对象:每个分段数组存储元素,若元素体积大,分段数量会减少,但随机访问逻辑不变,不过内存碎片可能增加(需结合实际场景权衡)。
总之,deque 是 STL 中 “平衡双端操作和随机访问” 的容器,在需要频繁操作两端且需随机访问的场景中,是比 vector 和 list 更优的选择。
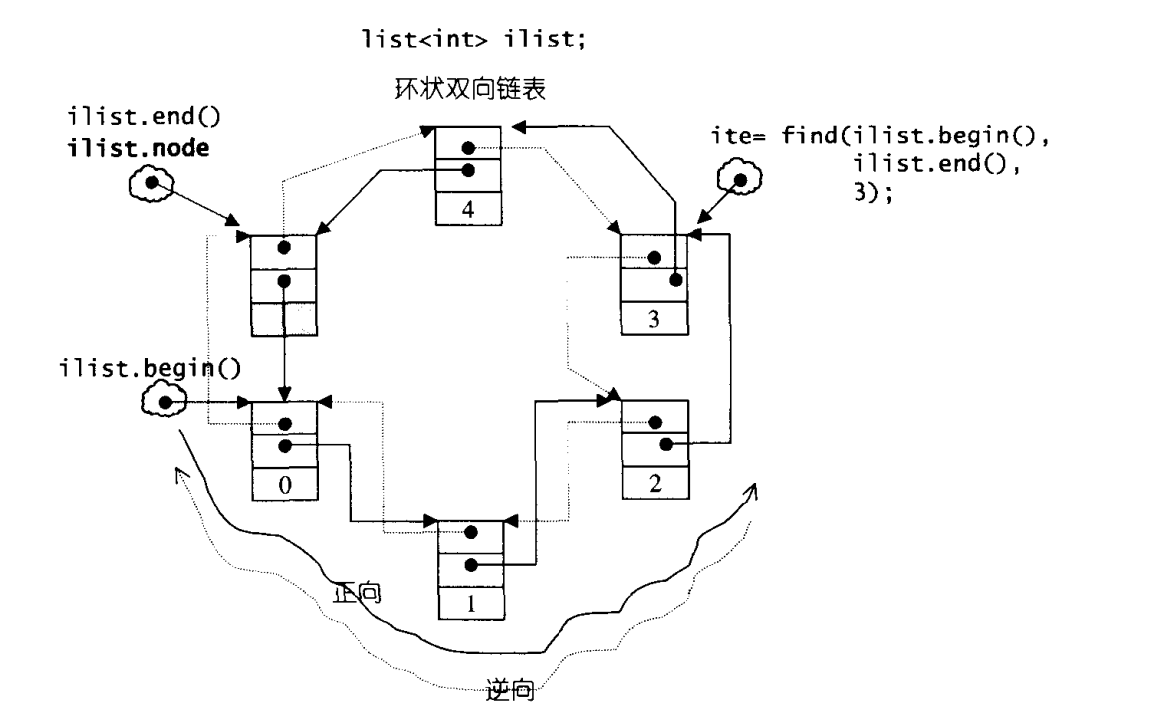
list(双向链表)
在 C++ STL 中,std::list 是一种双向链表(双向非循环链表) 容器,其元素通过节点间的指针连接,不要求内存连续。这种结构使其在任意位置的插入和删除操作上具有独特优势,以下从核心特性、底层原理、常用接口和适用场景等方面详细解析:
一、核心特性
-
双向链表结构
每个节点包含:- 数据域(存储元素值)
- 前驱指针(指向当前节点的前一个节点)
- 后继指针(指向当前节点的后一个节点)
首节点的前驱指针和尾节点的后继指针均为nullptr,不形成循环。
-
高效的插入与删除
- 在任意位置(头部、尾部、中间)插入或删除元素的时间复杂度为 O(1)(只需修改相邻节点的指针,无需移动其他元素)。
- 但查找目标位置需要遍历链表,时间复杂度为 O(n),因此 “查找 + 插入 / 删除” 的整体复杂度为 O (n)。
-
不支持随机访问
无法通过下标([])直接访问元素,必须从首节点或尾节点开始遍历(通过迭代器++/--移动),访问第 n 个元素的时间复杂度为 O (n)(这是与vector、deque的核心区别)。 -
内存动态分配
元素在堆上逐个分配内存,节点间无需连续,因此不会像vector那样因扩容导致大规模内存拷贝,但存在额外的指针内存开销(每个节点两个指针)。
二、底层原理(为何插入删除高效?)
list 的高效插入 / 删除源于其链表结构:
- 当已知插入 / 删除位置的迭代器时,操作仅需 3 步:
- 创建新节点(插入时)或标记待删除节点(删除时);
- 修改前一个节点的后继指针,指向新节点(插入)或下一个节点(删除);
- 修改新节点(插入)或下一个节点的前驱指针,指向合适的节点。
- 整个过程无需移动其他元素,仅涉及指针修改,因此效率极高。
例如,在节点 A 和 B 之间插入节点 C:
原链表:A <-> B
插入后:A <-> C <-> B
(仅需修改 A 的后继指针和 B 的前驱指针)
三、常用成员函数(核心接口)
list 提供了丰富的接口,尤其针对链表特性优化了插入、删除和移动操作:
| 类别 | 成员函数 | 功能描述 |
|---|---|---|
| 构造 / 析构 | list() | 默认构造空链表 |
list(n, val) | 构造包含 n 个 val 的链表 | |
list(beg, end) | 从迭代器范围 [beg, end) 构造链表(如从 vector 或数组初始化) | |
| 两端操作 | push_front(val) | 在头部插入元素(O (1)) |
push_back(val) | 在尾部插入元素(O (1)) | |
pop_front() | 删除头部元素(O (1),需确保链表非空) | |
pop_back() | 删除尾部元素(O (1),需确保链表非空) | |
| 任意位置操作 | insert(pos, val) | 在迭代器 pos 指向的位置前插入 val,返回新元素的迭代器(O (1)) |
erase(pos) | 删除迭代器 pos 指向的元素,返回下一个元素的迭代器(O (1)) | |
erase(beg, end) | 删除迭代器范围 [beg, end) 内的元素,返回下一个元素的迭代器(O (n)) | |
| 元素访问 | front() | 获取头部元素的引用(O (1)) |
back() | 获取尾部元素的引用(O (1)) | |
| 链表操作 | clear() | 清空所有元素(O (n)) |
size() | 返回元素个数(O (1),C++11 后支持,之前版本需遍历计数) | |
empty() | 判断是否为空(O (1)) | |
sort() | 对链表排序(内部实现为归并排序,O (n log n),不支持 std::sort 因为需要随机访问迭代器) | |
reverse() | 反转链表(O (n)) | |
splice(pos, list2) | 将链表 list2 的所有元素移动到当前链表 pos 位置前(O (1),无元素拷贝) |
四、适用场景(什么时候用 list?)
list 适合以下场景:
-
频繁在任意位置插入 / 删除元素
例如:实现链表式数据结构(如邻接表)、日志系统(需在中间插入修正记录)、 undo/redo 操作栈(频繁在头部插入历史记录)。 -
元素数量动态变化大,且无需随机访问
当不需要通过下标访问元素,仅需顺序遍历,且增删操作频繁时,list比vector(中间增删效率低)和deque(中间增删效率低)更合适。 -
需要高效移动元素块
通过splice成员函数可以 O (1) 时间移动整个链表或子链表(无元素拷贝,仅修改指针),适合实现链表合并、拆分等操作。
五、与 vector、deque 的对比
| 特性 | list | vector | deque |
|---|---|---|---|
| 底层结构 | 双向链表 | 连续动态数组 | 分段数组 + 中控数组 |
随机访问([]) | 不支持(O (n)) | 支持(O (1)) | 支持(O (1)) |
| 任意位置插入 / 删除 | O (1)(已知位置) | O (n)(需移动元素) | O (n)(需移动元素) |
| 内存连续性 | 不连续 | 连续 | 分段连续 |
| 内存开销 | 高(节点含指针) | 低(仅存储元素) | 中(分段管理) |
| 迭代器类型 | 双向迭代器 | 随机访问迭代器 | 随机访问迭代器 |
| 适用场景 | 频繁任意位置增删 | 频繁随机访问 | 频繁双端操作 + 随机访问 |
六、使用示例(代码演示)
#include <iostream>
#include <list>
#include <algorithm> // 用于 find 等算法int main() {// 1. 构造 list 并初始化std::list<int> lst1; // 空链表std::list<int> lst2(3, 5); // 3个5:[5,5,5]std::list<int> lst3(lst2.begin(), lst2.end()); // 从 lst2 复制:[5,5,5]// 2. 插入元素lst1.push_back(10); // 尾部插入:[10]lst1.push_front(20); // 头部插入:[20,10]auto it = lst1.begin(); // it 指向 20++it; // it 指向 10lst1.insert(it, 30); // 在 10 前插入 30:[20,30,10]// 3. 遍历元素(只能通过迭代器或范围 for)std::cout << "lst1 元素:";for (int val : lst1) {std::cout << val << " "; // 20 30 10}std::cout << std::endl;// 4. 删除元素lst1.pop_front(); // 删除头部:[30,10]it = std::find(lst1.begin(), lst1.end(), 30); // 查找 30 的迭代器if (it != lst1.end()) {lst1.erase(it); // 删除 30:[10]}// 5. 链表特有操作std::list<int> lst4 = {3, 1, 2};lst4.sort(); // 排序:[1,2,3]lst4.reverse(); // 反转:[3,2,1]std::cout << "lst4 排序反转后:";for (int val : lst4) {std::cout << val << " "; // 3 2 1}return 0;
}
七、注意事项
- 迭代器有效性:
list的迭代器在插入元素后仍有效(只需调整指针,节点地址不变);删除元素后,只有指向被删除节点的迭代器失效,其他迭代器仍可使用(这是list的重要优势)。 - 不支持
std::sort:std::sort要求随机访问迭代器,而list是双向迭代器,因此必须使用自身的sort()成员函数。 - 缓存不友好:由于元素内存不连续,CPU 缓存命中率低,遍历速度通常慢于
vector(即使两者时间复杂度均为 O (n))。
总之,list 是针对 “频繁任意位置增删” 优化的容器,在不需要随机访问的场景中,能显著提升操作效率。
---------------------------------------------------------------------------------------------------------------------------------
deque插入(insert)的底层原理
通过__index判断插入点位置,选择移动元素更少的方向(头部或尾部),体现 “短路径优先” 的优化思想。这段代码的注释清晰展现了deque中间插入的优化逻辑,即通过巧妙利用头尾操作的高效性,减少元素移动的数量,从而提升插入性能。
// 模板函数定义:在deque的中间位置插入单个元素的辅助函数
// 返回值:插入后新元素的迭代器
// 参数:__pos-插入位置迭代器;__x-要插入的元素值
template <class _Tp, class _Alloc>
typename deque<_Tp, _Alloc>::iterator
deque<_Tp,_Alloc>::_M_insert_aux(iterator __pos, const value_type& __x)
{// 计算插入点__pos相对于起始位置_M_start的偏移量(逻辑索引)// 用于判断插入点更靠近头部还是尾部difference_type __index = __pos - _M_start;// 复制要插入的元素(避免原元素被意外修改,确保值的稳定性)value_type __x_copy = __x;// 判断插入点是否更靠近头部(距离头部比距离尾部近)// 采用"短路径优先"策略,减少需要移动的元素数量if (size_type(__index) < this->size() / 2) {// 分支1:插入点靠近头部,从头部方向移动元素// 在头部插入一个当前头部元素的副本(利用deque头部插入高效的特性)// 此时头部会有一个重复元素,后续会通过移动覆盖push_front(front());// 定义迭代器:__front1指向新插入的头部副本元素iterator __front1 = _M_start;++__front1;// __front2指向__front1的下一个元素(原头部元素)iterator __front2 = __front1;++__front2;// 重新定位插入点__pos:因头部插入可能导致迭代器失效,通过索引重新计算__pos = _M_start + __index;// __pos1指向插入点的下一个元素(需要移动的起始位置)iterator __pos1 = __pos;++__pos1;// 将[__front2, __pos1)范围内的元素复制到__front1开始的位置// 效果:从头部方向将元素向后移动一个位置,为新元素腾出空间copy(__front2, __pos1, __front1);}else {// 分支2:插入点靠近尾部,从尾部方向移动元素// 在尾部插入一个当前尾部元素的副本(利用deque尾部插入高效的特性)// 此时尾部会有一个重复元素,后续会通过移动覆盖push_back(back());// 定义迭代器:__back1指向新插入的尾部副本元素iterator __back1 = _M_finish;--__back1;// __back2指向__back1的前一个元素(原尾部元素)iterator __back2 = __back1;--__back2;// 重新定位插入点__pos:因尾部插入可能导致迭代器失效,通过索引重新计算__pos = _M_start + __index;// 将[__pos, __back2]范围内的元素从后向前复制到__back1方向// 效果:从尾部方向将元素向后移动一个位置,为新元素腾出空间copy_backward(__pos, __back2, __back1);}// 在腾出的插入位置放入新元素的副本*__pos = __x_copy;// 返回指向新插入元素的迭代器return __pos;
}需要注意的是: vector 的 insert 操作可能导致迭代器失效,这是由 vector 底层连续内存的特性决定的。当插入元素引发内存重新分配或元素移动时,原有的迭代器、指针或引用可能指向无效内存,使用它们会导致未定义行为(如程序崩溃、数据错误)。
如何避免迭代器失效?
-
使用
insert的返回值更新迭代器
vector::insert会返回一个新的迭代器,指向插入的新元素。用这个返回值更新原迭代器,可避免失效:auto it = vec.begin() + 1; // 插入元素并获取新迭代器 it = vec.insert(it, 99); // it 现在指向新插入的99,有效 -
提前预留足够容量(
reserve)
若已知插入元素的数量,先用reserve(n)预留足够容量,避免插入时触发扩容:vec.reserve(100); // 预留100个元素的空间 // 后续插入不超过100个元素时,不会触发扩容 -
插入后重新获取迭代器
若无法提前预留容量,插入后通过索引或begin()重新计算迭代器:vec.insert(vec.begin() + 1, 99); auto it = vec.begin() + 1; // 重新获取,有效
