【计算机组成原理·信息】2数据①
1.数据如何表示?
使用一种“编码”方式,将人类世界的“真值”➡️计算机世界的“机器数”,这个过程就叫“表示”。
真值:人类习惯书写和理解的原始数值。它带有正负号、小数点。
例如:-5,+10,-3.75, +0.0,-0.0。
机器数:真值在计算机内部的二进制表示形式。就是一串由 0 和 1 组成的序列。
机器数的位数被称为机器字长。
例如,真值 -5 的某种机器数表示可能是 10000101(最高位1表示负)。
编码:将真值转换为机器数(或反之)的一套规则和标准。它是一座桥梁。解决了“符号”和“小数点”的数字化问题。
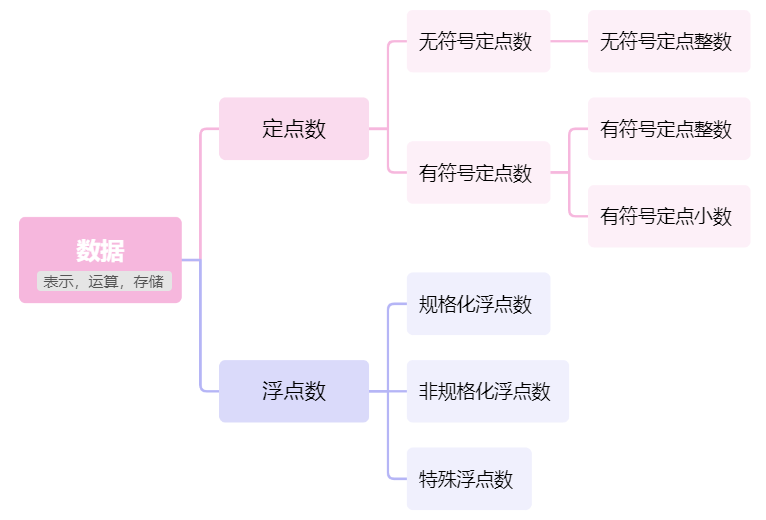
①无符号定点数编码:最直接的二进制规则,所有位都表示数值。
②有符号定点数编码:原码、反码、补码、移码。它们规定了符号位和数值位如何组合。
③浮点数编码:IEEE 754标准。它规定了如何把实数分解成符号、阶码、尾数三部分。
(除了数的编码,还有非数值编码:ASCII码(字符)、BCD码(十进制))
1.1.进位计数制
学习进位计数制是为了理解如何将“真值”➡️“机器数”。
1.1.1.r进制数
1.1.1.1.基数r
一种计数制中,每个数码位所用到的基本符号的个数,也就是一个位能有几位数字,称为基数。
| r | 符号 | 进制书写规范 |
|---|---|---|
| r=2 二进制 (Binary) | 0,1 | 下标法: 字母后缀:1011B |
| r=8 八进制 (Octal) | 0,1,2,3,4,5,6,7 | 下标法: 字母后缀:17O |
| r=10 十进制 (Decimal) | 0,1,2,3,4,5,6,7,8,9 | 字母后缀:123D |
| r=16 十六进制 (Hexadecimal) | 0,1,2,3,4,5,6,7,8,9, A=10,B=11,C=12,D=13,E=14,F=15 | 下标法: 字母后缀:1FH 前缀法(常见于程序代码): |
计算机采用二进制的原因:
①可使用具有两个稳定状态的物理器件表示(高/低电平,电容充/放电)。
②0/1可对应逻辑假/真,便于实现逻辑运算。
③可使用逻辑门电路方便地实现算术运算。
💎练习题

为何使用八进制和十六进制:与二进制转换方便,便于程序员阅读和记录机器代码。
1.1.1.2.位权rⁿ
数码在不同位置上所代表的数值权重,即系数应乘的幂次。
整数部分:从右向左,第位(
从
开始)的位权为
小数部分:从左向右,第位(
从
开始)的位权为
1.1.1.3.数值计算公式
一个进制数
对应的十进制值为
1.1.2.数制转换
1.1.2.1.² ⁸ ¹⁶→¹⁰
方法:使用数值计算公式。
示例:
二进制 → 十进制
八进制 → 十进制
十六进制 → 十进制
1.1.2.2.²⇄ ⁸ ¹⁶
方法:由于一位八进制数对应三位二进制数,一位十六进制数对应四位二进制数。
二进制 → 八/十六进制的方法是:①以小数点为界,向左、右分组。②八进制,每3位一组,不足补0;十六进制,每4位一组,不足补0。③将每组二进制数转换为对应的八、十六进制数。
八/十六进制 → 二进制的方法是:将每一位八、十六进制数,展开为对应的3位、4位二进制数即可。
示例:
1.1.2.3.¹⁰→² ⁸ ¹⁶
方法:整数部分采用除基取余法转换;小数部分采用乘基取整法转换。
①除基取余法:将十进制整数连续除以基数,直到商为0。
先得到的余数是低位,后得到的是高位。(先得到的写在小数点那一边)
②乘基取整法:将十进制小数连续乘以基数r,直到积为整数或达到所需精度。
先得到的整数部分是高位,后得到的是低位。(先得到的写在小数点那一边)
技巧(拼凑法):对于熟悉的数字,可用位权拼凑。

示例:
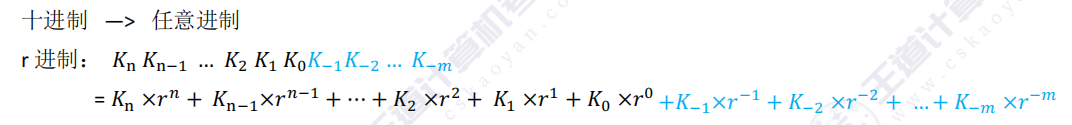


💎练习题

1.2.定点数表示
定点数表示:定点数的“真值”➡️“机器数”

注意:这里不能表示所有定点数,只能表示小数点固定在数值位后或小数点固定在符号位后的定点数。比如说广义上的定点数是包含9.7的,但是这里的“定点数表示”无法表示出9.7,如果要表示,需要把9.7转换为浮点数表示。
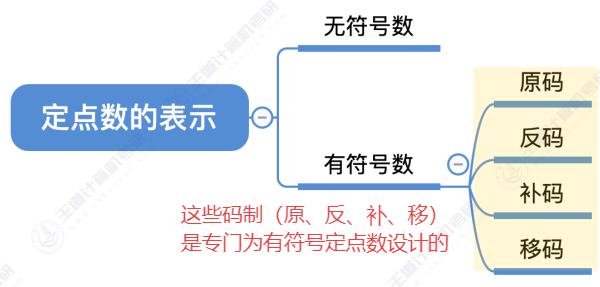
✅ 无符号定点数:用直接二进制表示(可视为原码)
✅ 有符号定点数:现代计算机主要用补码,但原码、反码、移码都有其特定应用场景
1.2.1.无符号定点数
定义:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
通常只讨论无符号整数,几乎没有“无符号小数”的概念。
表示范围:若用位二进制表示无符号数,其表示范围为
,表示个数有
个。例如,8位无符号数,范围为
0 (0000 0000) 到 255 (1111 1111)。
(只有)无符号定点整数
1️⃣所有二进制位均为数值位,无符号位。默认符号为正。
2️⃣位无符号整数范围:
。
3️⃣例如8位无符号整数的最小值为0000 0000 → 0;最大值为1111 1111 → 255。
💎练习题

