当前位置：首页 > ai >正文

PAT 1068 Find More Coins

ai 2025/8/18 7:36:59

在这里插入图片描述

这一题的意思是说在N个硬币中选择，使得面额等于M，如果有多种情况，输出字典序从小到大排列的顺序，如果没有选择能使得最后的面额等于M那么就输出No Solution
看题意很明显能想出是选与不选，可以采用dfs递归回溯遍历来枚举所有的情况，当出现等于M的序列后就把它放入到ans数组中。
在这个递归回溯的过程中可以采用挂缓存表的方法，即记忆化搜索，
用缓存表，存储dp[cnt][w]即能不能从第cnt个开始，质量为w，凑出最终的序列是M
如果可以的话，就标记为dp[cnt][w]=1;不可以的话，就标记dp[cnt][w]=0，
判断该状态可不可以的方法就是判断序列数有没有增加

if(ans.size()>nowsize) {dp[cnt][w] = 1;} else {dp[cnt][w] = 0;}

因为数据范
围是N<10^4,那么采用dfs是很容易超时的，因此需要剪枝

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>using namespace std;
int N;
int M;
int v[10001];
int dp[10001][100]; 
vector<vector<int>> ans; 
void dfs(int cnt,int w,vector<int>& q)
{if(cnt>N){return;}if(w>M){return ;}if(w==M){ans.push_back(q);return;}if(dp[cnt][w]==1){//说明可以 }if(dp[cnt][w]==0){return ;}int nowsize=ans.size();q.push_back(v[cnt+1]);dfs(cnt+1,w+v[cnt+1],q);q.pop_back();dfs(cnt+1,w,q);if(ans.size()>nowsize) {dp[cnt][w] = 1;} else {dp[cnt][w] = 0;}}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>N>>M;for(int i=1;i<=N;i++){cin>>v[i];}memset(dp,-1,sizeof(dp));vector<int> q;q.push_back(v[1]);dfs(1,v[1],q);q.pop_back();dfs(1,0,q);if(ans.size()==0){cout<<"No Solution";return 0;}for(int i=0;i<ans.size();i++){sort(ans[i].begin(),ans[i].end());}sort(ans.begin(), ans.end());bool flag=0;for(int j=0;j<ans[0].size();j++){if(flag==0){cout<<ans[0][j];flag=1;}else{cout<<" "<<ans[0][j];}}	cout<<endl;return 0;}

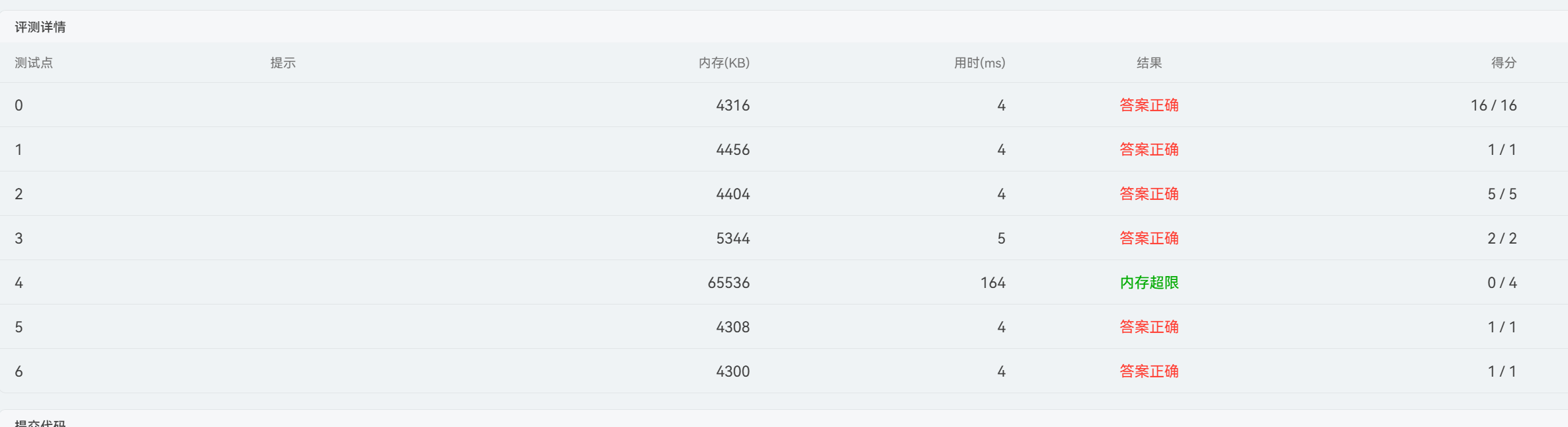
在这里插入图片描述
因为采用的是二维数组来保存，因此容易出现了内存超限。
最合适的方法应该采用dp table的方法，因为题目上的选与不选，每一个硬币只能选一次，这是很明显的01背包
01背包的核心是写出状态转移方程，明确状态转移方程的含义

bool dp[10001][100];

dp[N][M]的意思从前N个硬币选出M个，如果能为true，如果不能为false
那么就可以套用01背包的模板了

	for(int i=1;i<=N;i++)//从前i个里面选择{for(int j=0;j<=M;j++)//面值为j{if(v[i]<=j&&dp[i-1][j-v[i]])//如果当前面置是小于等于j，并且前i-1个中能选择出来j-v[i]的面值。{dp[i][j]=true;//}else//如果不能，那么从前i个里面选择面值为j，实际上就相当于从从i-1里面选择面值为j{dp[i][j]=dp[i-1][j];}}}

要注意的是这样的选择，是无序的，而题目上想让我们输出字典序最小的满足题意的序列。

sort(v+1,v+1+N,cmp);

因此，我们应该在递推状态转移方程前面对硬币面额进行一个从大到小的排序，
为啥要从大到小排序呢，因为我们在后面想得到dp[N][M]必须是逆序，面值的序列是字典序从小到大。

int j=M;for(int i=N;i>=1;i--){if(j>=v[i]&&dp[i-1][j-v[i]]){ans.push_back(v[i]);j-=v[i];}}

当把所有的值放入到序列中后
按题目要求输出即可

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>using namespace std;
int N;
int M;
int v[10001];
bool dp[10001][100]; 
//要清楚这个dp方程的含义
//什么呢，dp[i][j]从前i个中选出质量为j 
//如果能选出就为true，不能为false 
bool cmp(int a,int b)
{return a>b;
}
vector<int> ans;
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>N>>M;for(int i=1;i<=N;i++){cin>>v[i];}sort(v+1,v+1+N,cmp);dp[0][0]=true;//dp[0][1]=false;for(int i=1;i<=N;i++){for(int j=0;j<=M;j++){if(v[i]<=j&&dp[i-1][j-v[i]]){dp[i][j]=true;}else{dp[i][j]=dp[i-1][j];}}} if(dp[N][M]!=true){cout<<"No solution";return 0;}int j=M;for(int i=N;i>=1;i--){if(j>=v[i]&&dp[i-1][j-v[i]]){ans.push_back(v[i]);j-=v[i];}}// sort(ans.begin(),ans.end());for(int i=0;i<ans.size();i++){if(i==0){cout<<ans[i];}else{cout<<" "<<ans[i];}}return 0;}