当前位置： 首页 > ai >正文

数据结构——栈和队列oj练习

ai 2025/8/18 5:38:56

225. 用队列实现栈 - 力扣（LeetCode）

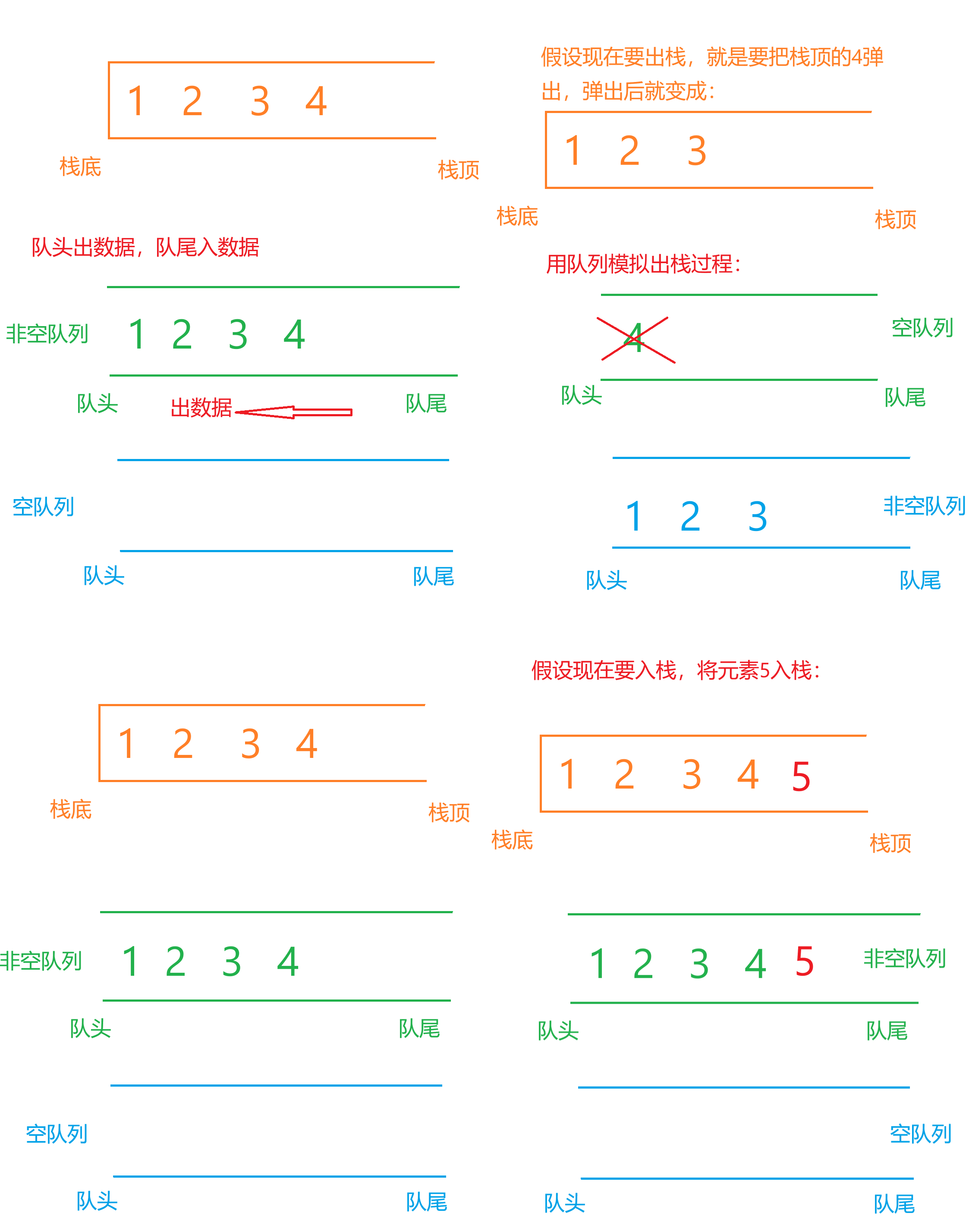
这一题需要我们充分理解队列和栈的特点。

队列：队头出数据，队尾入数据。

栈：栈顶出数据和入数据。

我们可以用两个队列实现栈，在这过程中，我们总要保持其中一个队列为空。如果我们出栈，也就是要将栈顶元素弹出，就相当于对非空队列进行操作，就是要把非空队列的队尾元素弹出队列。但是队列的队尾是不能出数据的，想要让队尾数据出队列，就要让这个数据到达队头，同时我们还要保留其他的数据，就需要用到另一个队列来保存。

所以说，我们要用队列模拟出栈过程，就要把非空队列中的数据不断弹出放到另一个队列中，直到非空队列中的数据个数变成1，保留下这个数据的值，再将这个数据从队列中弹出。

对于取栈顶元素过程，大部分代码可以复用出栈的代码。或者我们可以发现栈顶元素就是非空队列的队尾元素，我们直接取出非空队列的队尾元素即可。

对于入栈过程，对于栈，我们直接将数据放到非空队列的队尾即可。

typedef int Qdatatype;typedef struct QueueNode
{Qdatatype data;struct QueueNode* next;
}QueueNode;//队列的结构定义：
typedef struct Queue
{QueueNode* phead;//队头QueueNode* ptail;//队尾int size;//队列中有效数据个数
}Queue;//初始化
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}//销毁
void QueueDesTroy(Queue* pq)
{QueueNode* pcur = pq->phead;while (pcur){QueueNode* pnext = pcur->next;free(pcur);pcur = pnext;}pq->phead = pq->ptail = NULL;pq->size = 0;
}//入队列
//入队列是在队尾入的，所以入队列相当于链表的尾插
void QueuePush(Queue* pq, Qdatatype x)
{assert(pq);//申请新的节点空间QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));newnode->next = NULL;newnode->data = x;//尾插//如果此时队列中一个元素都没有if (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else//队列本来就有元素{pq->ptail->next = newnode;pq->ptail = newnode;}(pq->size)++;
}//判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}//出队列
//出队列是在队头出的，相当于链表的头删
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//如果链表中只有一个元素if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else//直接头删{QueueNode* newhead = pq->phead->next;free(pq->phead);pq->phead = newhead;}(pq->size)--;
}//取队头数据
Qdatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}//取队尾数据
Qdatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;
}//队列有效元素个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}//=========前面为队列的实现===========
//栈的结构
typedef struct 
{Queue q1;Queue q2;
} MyStack;//栈的初始化
MyStack* myStackCreate() {MyStack* stack=(MyStack*)malloc(sizeof(MyStack));QueueInit(&(stack->q1));QueueInit(&(stack->q2));return stack;
}
//入栈
void myStackPush(MyStack* obj, int x) 
{Queue* empty=&(obj->q1);Queue* nonempty=&(obj->q2);if(QueueEmpty(&(obj->q2))){empty=&(obj->q2);nonempty=&(obj->q1);}QueuePush(nonempty,x);
}
//出栈
int myStackPop(MyStack* obj) 
{Queue* empty=&(obj->q1);Queue* nonempty=&(obj->q2);if(QueueEmpty(&(obj->q2))){empty=&(obj->q2);nonempty=&(obj->q1);}while(QueueSize(nonempty)!=1)//让非空队列中的元素不停地出栈直到栈中只有一个元素{//将元素放到原来是空的队列中QueuePush(empty,QueueFront(nonempty));//出队列QueuePop(nonempty);}int ret=QueueFront(nonempty);QueuePop(nonempty);return ret;
}
//取栈顶元素:两种方法
//方法一：
int myStackTop(MyStack* obj) 
{Queue* empty=&(obj->q1);Queue* nonempty=&(obj->q2);if(QueueEmpty(&(obj->q2))){empty=&(obj->q2);nonempty=&(obj->q1);}while(QueueSize(nonempty)!=1)//让非空队列中的元素不停地出栈直到栈中只有一个元素{//将元素放到原来是空的队列中QueuePush(empty,QueueFront(nonempty));//出队列QueuePop(nonempty);}int ret=QueueFront(nonempty);QueuePush(empty,ret);QueuePop(nonempty);return ret;
}
//方法二：
int myStackTop(MyStack* obj) 
{Queue* empty=&(obj->q1);Queue* nonempty=&(obj->q2);if(QueueEmpty(&(obj->q2))){empty=&(obj->q2);nonempty=&(obj->q1);}return QueueBack(nonempty);
}//判断栈是否为空
bool myStackEmpty(MyStack* obj) {return QueueEmpty(&(obj->q1)) && QueueEmpty(&(obj->q2));
}
//销毁
void myStackFree(MyStack* obj) 
{QueueDesTroy(&(obj->q1));QueueDesTroy(&(obj->q2));free(obj);obj=NULL;
}

232. 用栈实现队列 - 力扣（LeetCode）

我们是可以用两个栈实现队列的结构的。具体实现方法如下：

我们定义两个栈，一个栈A是专门用来插入数据的，另一个栈B是专门用来出数据的。当我们要插入数据的时候，直接往A中插入即可，当我们要删除数据的时候，要先检查B是否为空，如果B为空，就讲A中的数据全部放入B中，如果B不为空，就直接对B进行出栈操作。

typedef int stdatatype;//定义栈的结构：
typedef struct Stack
{stdatatype* arr;int top;//指向栈顶的后一个位置，也可以表示有效数据个数int capacity;//栈中的最大容量
}ST;
//初始化
void STInit(ST* ps)
{assert(ps);//防止后续空指针解引用ps->arr = NULL;ps->top = 0;//如果使top=0，那么top指向栈顶元素的后一个位置，//如果想让top指向栈顶元素,就要让top初始化为-1ps->capacity = 0;
}//销毁
void STDesTroy(ST* ps)
{assert(ps);free(ps->arr);ps->arr = NULL;ps->capacity = ps->top = 0;
}//入栈——栈顶
void STPush(ST* ps, stdatatype x)
{assert(ps);//先判断是否需要扩容if (ps->top == ps->capacity){//需要扩容int newcapacity = ps->capacity > 0 ? 2 * ps->capacity : 4;stdatatype*tmp = (stdatatype*)realloc(ps->arr, newcapacity * sizeof(stdatatype));ps->arr = tmp;ps->capacity = newcapacity;}ps->arr[(ps->top)++] = x;
}//栈是否为空
bool STEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈———栈顶
void STPop(ST* ps)
{assert(ps);//出栈之前先判空assert(ps->top);ps->top--;
}//取栈顶元素
stdatatype STTop(ST* ps)
{assert(ps);//去栈顶元素之前先判空assert(ps->top);return ps->arr[ps->top - 1];
}//获取栈中有效元素个数
int STSize(ST* ps)
{assert(ps);return ps->top;
}//================以上全是栈的实现=============
typedef struct 
{ST pushst;ST popst;
} MyQueue;MyQueue* myQueueCreate() 
{MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));STInit(&(obj->pushst));STInit(&(obj->popst));return obj;
}
void myQueuePush(MyQueue* obj, int x) 
{STPush(&(obj->pushst),x);
}int myQueuePop(MyQueue* obj) 
{if(!STEmpty(&(obj->popst))){int ret=STTop(&(obj->popst));STPop(&(obj->popst));return ret;}else{while(!STEmpty(&(obj->pushst))){STPush(&(obj->popst),STTop(&(obj->pushst)));STPop(&(obj->pushst));}int ret=STTop(&(obj->popst));STPop(&(obj->popst));return ret;}
}int myQueuePeek(MyQueue* obj) 
{if(!STEmpty(&(obj->popst))){int ret=STTop(&(obj->popst));return ret;}else{while(!STEmpty(&(obj->pushst))){STPush(&(obj->popst),STTop(&(obj->pushst)));STPop(&(obj->pushst));}int ret=STTop(&(obj->popst));return ret;}}bool myQueueEmpty(MyQueue* obj) 
{return STEmpty(&(obj->pushst)) && STEmpty(&(obj->popst));
}void myQueueFree(MyQueue* obj) 
{STDesTroy(&(obj->pushst));STDesTroy(&(obj->popst));free(obj);
}

622. 设计循环队列 - 力扣（LeetCode）

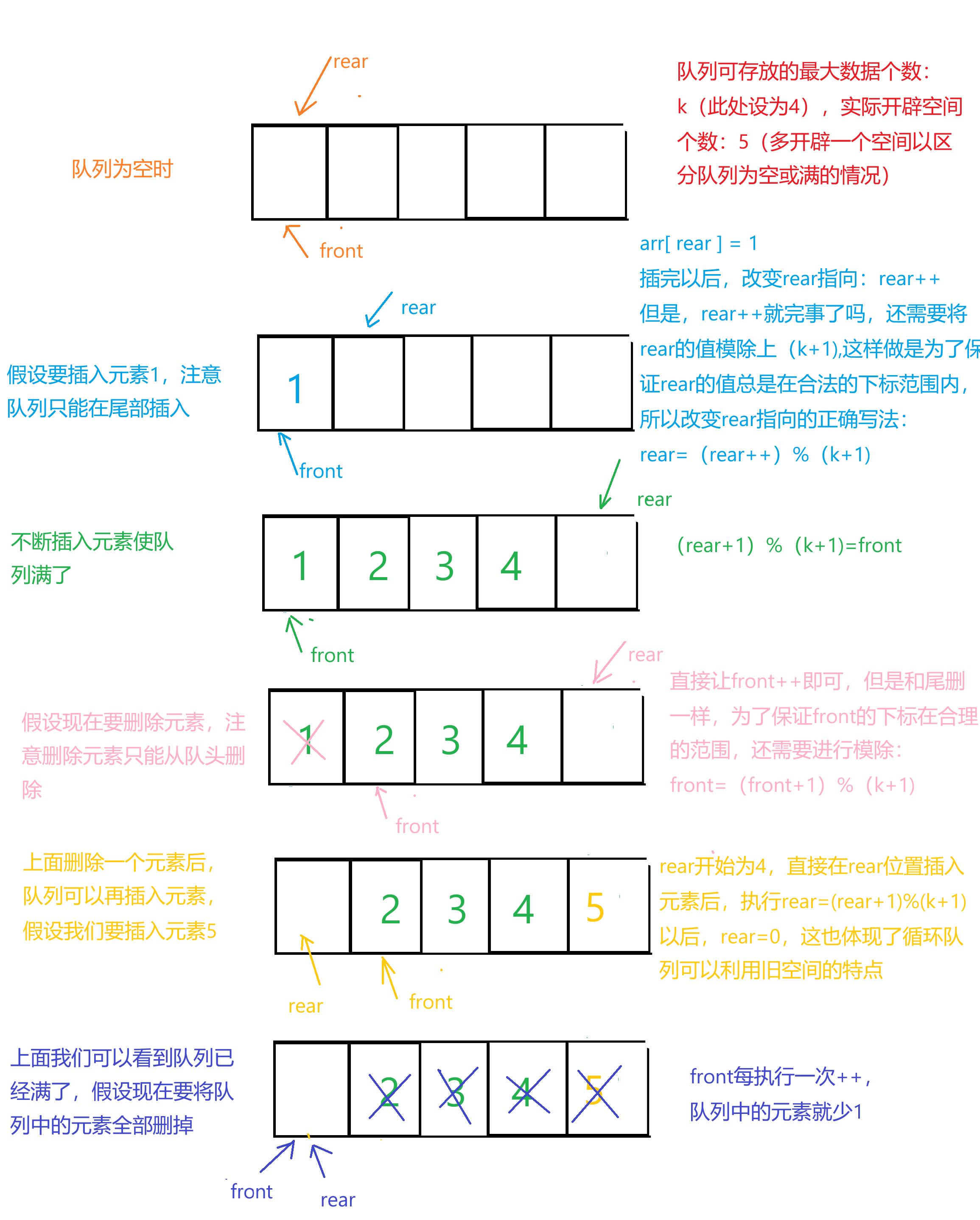
//我们用数组的结构设计循环队列
//这一题要善于运用模除的运算从而达到利用旧空间的效果
typedef struct {int front;int rear;int*arr;int capacity;
} MyCircularQueue;bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{return obj->rear==obj->front;
}bool myCircularQueueIsFull(MyCircularQueue* obj) 
{return (obj->rear+1)%(obj->capacity)==obj->front;
}MyCircularQueue* myCircularQueueCreate(int k) 
{MyCircularQueue*cirque=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));cirque -> front=0;//指向 队头元素（即下一个要出队的元素）。cirque -> rear= 0;//rear指向的是队尾元素的下一个位置cirque -> arr=(int*)malloc(sizeof(int)*(k+1));//多开辟一个空间以区分队列满和空的状态cirque->capacity=k+1;return cirque;
}
//尾插
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{if(!myCircularQueueIsFull(obj)){obj->arr[(obj->rear)++]=value;obj->rear=(obj->rear)%(obj->capacity);return true;}return false;
}
//头删
bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{if(myCircularQueueIsEmpty(obj)){return false;}obj->front= ( obj->front+1)%(obj->capacity);return true;
}int myCircularQueueFront(MyCircularQueue* obj) 
{if(myCircularQueueIsEmpty(obj)){return -1;}return obj->arr[obj->front];
}int myCircularQueueRear(MyCircularQueue* obj) 
{if(myCircularQueueIsEmpty(obj)){return -1;}return obj->arr[(obj->rear-1+obj->capacity)%(obj->capacity)];
}void myCircularQueueFree(MyCircularQueue* obj) {free(obj->arr);free(obj);
}

解析：图中我们解释了如何插入和删除元素

设计循环双端队列

双端队列（Deque，Double-Ended Queue）是一种支持 队头（front）和队尾（rear）两端高效插入和删除 的数据结构。

上一题我们实现了循环队列的实现，有了上一题的基础，我们就能利用循环队列来实现双端队列：

//双端队列中：
//front 直接指向当前队头元素（即下一个从队头出队的元素）。
//rear 指向队尾的下一个空位（即下一个插入队尾的位置）。
//在队头插入数据时，要先改变front指向；同理，在队尾插入元素以后，要改变rear的指向
//然而，插入元素后不能同时让front和rear同时递增或同时递减
//我们就使在队头插入数据后，front--，队尾插入数据后rear++typedef struct {int front;int rear;int capacity;int*arr;
} MyCircularDeque;MyCircularDeque* myCircularDequeCreate(int k) 
{MyCircularDeque* obj=(MyCircularDeque*)malloc(sizeof(MyCircularDeque));obj->front=obj->rear=0;obj->arr=(int*)malloc(sizeof(int)*(k+1));obj->capacity=k+1;return obj;
}bool myCircularDequeIsEmpty(MyCircularDeque* obj) 
{return obj->rear==obj->front;
}bool myCircularDequeIsFull(MyCircularDeque* obj) 
{return (obj->rear+1)%(obj->capacity)==obj->front;
}
//头插
bool myCircularDequeInsertFront(MyCircularDeque* obj, int value) 
{if(myCircularDequeIsFull(obj)){return false;}//front指向的是队头元素，所以我们再进行头插时，需要先改变队头指向obj->front=(obj->front-1+obj->capacity)%(obj->capacity);obj->arr[obj->front]=value;return true;
}bool myCircularDequeInsertLast(MyCircularDeque* obj, int value) 
{if(myCircularDequeIsFull(obj)){return false;}obj->arr[obj->rear]=value;//改变rear指向obj->rear=(obj->rear+1)%(obj->capacity);return true;
}bool myCircularDequeDeleteFront(MyCircularDeque* obj) 
{if(myCircularDequeIsEmpty(obj)){return false;}//插入元素是让front--，那么删除元素就要让front++obj->front=(obj->front+1)%(obj->capacity);return true;
}bool myCircularDequeDeleteLast(MyCircularDeque* obj) 
{if(myCircularDequeIsEmpty(obj)){return false;}obj->rear=(obj->rear-1+obj->capacity)%(obj->capacity);return true;
}int myCircularDequeGetFront(MyCircularDeque* obj) 
{if(myCircularDequeIsEmpty(obj)){return -1;}return obj->arr[obj->front];
}int myCircularDequeGetRear(MyCircularDeque* obj) 
{if(myCircularDequeIsEmpty(obj)){return -1;}return obj->arr[(obj->rear-1+obj->capacity)%(obj->capacity)];
}void myCircularDequeFree(MyCircularDeque* obj) 
{free(obj->arr);obj->arr=NULL;obj->front=obj->rear=obj->capacity=0;free(obj);obj=NULL;
}

http://www.xdnf.cn/news/17977.html

相关文章：

  • 深度解析 Spring Bean 生命周期
  • 【网络安全】Webshell的绕过——绕过动态检测引擎WAF-缓存绕过（Hash碰撞）
  • 《P4180 [BJWC2010] 严格次小生成树》
  • MySQL 插入数据提示字段超出范围？一招解决 DECIMAL 类型踩坑
  • 安卓11 12系统修改定制化_____修改运营商版本安装特定应用时的默认规则
  • 机器学习相关算法：回溯算法 贪心算法 回归算法(线性回归) 算法超参数 多项式时间 朴素贝叶斯分类算法
  • 一文速通Python并行计算：14 Python异步编程-协程的管理和调度
  • C语言：文件操作详解
  • 后量子密码算法SLH-DSA介绍及开源代码实现
  • Java8~Java21重要新特性
  • C++ 最短路Dijkstra
  • CodeBuddy IDE深度体验：AI驱动的全栈开发新时代
  • Maven下载和配置-IDEA使用
  • 【算法】——力扣hot100常用算法技巧
  • 使用IntersectionObserver实现页面右侧运营位区域固定，和页面列表数据分页加载
  • JetPack系列教程（七）：Palette——让你的APP色彩“飞”起来！
  • 【大语言模型 02】多头注意力深度剖析：为什么需要多个头
  • 后量子密码算法ML-DSA介绍及开源代码实现
  • 【DL学习笔记】常用数据集总结
  • 微服务架构实战指南：从单体应用到云原生的蜕变之路
  • 56. 合并区间
  • 【Java基础面试题】数据类型
  • PAT乙级_1085 PAT单位排行_Python_AC解法_含疑难点
  • C语言（11）—— 数组（超绝详细总结）
  • C++基础——内存管理
  • QT基础入门
  • Tomcat Server 组件原理
  • 肖臻《区块链技术与应用》第23-26讲 - The DAO事件、BEC事件、反思和总结
  • select、poll 和 epoll
  • RK3568 NPU RKNN（二）：RKNN-ToolKit2环境搭建