当前位置：首页 > ai >正文

旋转位置编码-ROPE简单理解

ai 2025/7/21 13:52:56

旋转位置编码-ROPE

什么是旋转位置编码

众所周知，transformer本身在进行注意力计算时是位置无关的。然而，现实情况下，大多数任务都会对特征的顺序有要求。因此，transformer在进行位置计算时就需要位置编码，最早是绝对位置编码，随后是可学习的位置编码，然而前两者只能在训练过的序列长度上表现好，因此最后进化到了旋转位置编码。

综上所述，旋转位置编码就是用于transformer的一种位置编码，且在此刻看来是比较优秀的一种位置编码。

旋转位置编码的核心思想是将特征表示为复数进行旋转，这样一来，在计算注意力的过程中，就能够实现动态相对位置感知。具体原理将稍后介绍

旋转位置编码怎么实现的

首先，我们明确一下前置条件。本次对旋转位置编码的介绍是对文本的编码，输入的特征形状为[B, L, D] 其中B为batchsize，L为序列长度，D为特征。另外，此处我们默认B为1，并且可以简单将L理解为每一个字，D理解为该字的特征。例如，我们将输入“我是一个人”转化为特征表示之后，就可以得到：
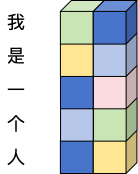
在这里插入图片描述

一个B为1（深度方向），L为5（纵向），D为2（横向）的特征。

随后，我们再来确定一件事，那就是位置编码中的“位置”，指的是L这个维度上的位置关系，即“我是一个人”这五个字之间的位置关系。旋转位置编码也是如此。

那么旋转位置编码在应用时的大致流程如下：

给L上的token编号，比如上述例子中，“我”是0号，“人”是4号
根据位置编号，生成旋转角度，这里的旋转角度有个固定的映射关系，通常为 $θm(i)=m100002i/d\theta_m^{(i)} = \frac{m}{10000^{2i/d}}$ ，其中m为1中提到的编号，d为特征的长度，在上述例子中d应该等于2，i则是d中特征的编号
根据角度生成包含cos和sin的旋转矩阵
将旋转矩阵应用到attention机制中的Q和K上

注意，此处并未解释为什么需要生成“旋转”矩阵，仅描述了旋转位置编码的应用流程。

下面我们将简单介绍其原理

旋转位置编码的原理

观察旋转角度的映射公式可以发现，假设我们固定i，那么随着m变大，角度是单调递增的，那也就意味着，只考虑位置信息时，旋转位置编码的注意力权重随距离呈现**近似单调衰减。**如图：

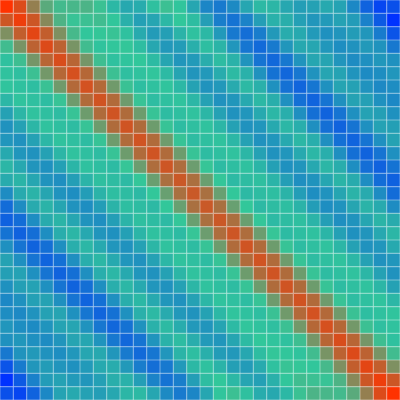
在这里插入图片描述

当有上述例子中L为30，D为32时，特征可视化如图。虽然注意力在衰减，但是为什么有周期性变化？这是其公式决定的，上面我们只提到了怎么计算旋转角，但是并没有提到真正应用时注意力是怎么计算的。下面我们将直接看代码来进行解释：

import torch
import torch.nn as nn
import mathclass RotaryPositionalEncoding(nn.Module):def __init__(self, dim_model, max_seq_len=512):super().__init__()self.dim_model = dim_modelself.max_seq_len = max_seq_len# 生成旋转矩阵的 cos 和 sin 编码self.register_buffer('freqs_complex', self._build_freqs(max_seq_len, dim_model))def _build_freqs(self, max_seq_len, dim_model):# 生成频率基底：1 / (10000^(2i/d)) => exp(-2i * log(10000) / d)inv_freq = 1.0 / (10000 ** (torch.arange(0, dim_model, 2).float() / dim_model))# 生成位置索引positions = torch.arange(max_seq_len).float()# 计算角度：t * inv_freqfreqs = torch.outer(positions, inv_freq)# 转换为复数：cosθ + i*sinθfreqs_complex = torch.polar(torch.ones_like(freqs), freqs)return freqs_complexdef apply_rotary_pos_emb(self, t, freqs_complex):# t: [batch_size, heads, seq_len, dim]# freqs_complex: [seq_len, head_dim // 2]# 将词向量拆分为实部和虚部（交替维度）t_reshaped = t.float().reshape(*t.shape[:-1], -1, 2)t_complex = torch.view_as_complex(t_reshaped)# 扩展 freqs_complex 以匹配 t 的形状freqs_complex = freqs_complex.unsqueeze(0).unsqueeze(1)  # [1, 1, seq_len, dim//2]t_rotated = t_complex * freqs_complex  # 逐元素复数乘法（旋转）# 恢复原始形状t_out = torch.view_as_real(t_rotated).reshape_as(t).type(t.dtype)return t_outdef forward(self, x, positions=None):"""x: [batch_size, seq_len, dim]positions: [seq_len] 或 None，表示每个 token 的位置索引"""if positions is None:positions = torch.arange(x.size(1), device=x.device)# 获取对应位置的旋转编码freqs_complex = self.freqs_complex[positions]# 将旋转编码应用到输入 x 上x_rotated = self.apply_rotary_pos_emb(x, freqs_complex)return x_rotated