贝叶斯分类器的相关理论学习
一、贝叶斯决策
条件风险:
其中
是总的类别标记,
是将样本
误分类成
所产生的损失,
是样本。
总体风险:
其中
为最小化总体风险的判定准则。
最小了的话,那么 R(h) 就最小了,即只需要选出每个样本上条件风险最小的类别标记
该公式被称为贝叶斯最优分类器,对应的
叫做贝叶斯风险。
即为分类器的最好性能。
最小化分类错误率的贝叶斯最优分类器为:
就相当于选择后验率最大的类别标记。
二、极大似然估计(结合概率论理解)
通俗来说就是条件概率的连乘。
和概率论中一样,由于连乘容易下溢,一般都是取对数之后在继续求极大似然。
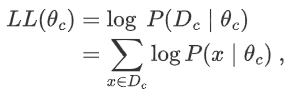
要求
的极大似然估计,就相当于就上述函数的极值。
三、朴素贝叶斯分类器
基本的理解就可以完全按照概率论中的贝叶斯公式来理解,分一下离散和连续两种情况的
的计算方式:
离散:目标样本数 / 总样本数;
连续:
其中的理解还是与数学概率论中相同;
四、半朴素贝叶斯分类器
独依赖:每个属性在各自的类别外最多依赖一个其他属性。
超父属性:假设所有属性都依赖于同一个属性。
属性依赖:
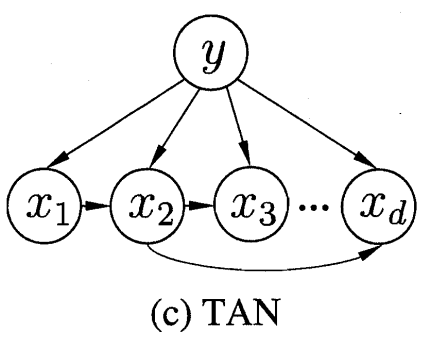
:是将每个属性作为超父来构建
。
五、贝叶斯网(信念网)
贝叶斯网结构上就是一个有向无环图。
在网络中每个属性都和它的非后裔属性独立,其联合概率分布为:
其中
是
的父节点。
道德图:即把有向图中的所有
型结构的两个父节点连上,再把所有的有向边改为无向边。
“最小描述长度”准则:一般通常情况下我们是通过评分函数来寻找最好的贝叶斯网络(基于信息论准则),找一个以最短编码长度描述训练数据的模型。
评分函数:
其中, 是贝叶斯网的参数个数,
表示描述每个参数
所需要的字节数。
注:贝叶斯网在推理的时候是按照马尔科夫链的原理来的。
