当前位置：首页 > ai >正文

深度神经网络原理学习记录

ai 2025/7/21 7:59:14

本人不是AI领域从业者，了解这方面的知识只是出于好奇。

以下这个简单的深度神经网络代码是AI写的，可以帮助理解原理：

// 简单神经网络类
class SimpleNeuralNetwork {
public:// 构造函数：初始化网络参数SimpleNeuralNetwork(): w1(0.1), b1(0.1),   // 输入层到隐藏层的权重和偏置，初始化为0.1w2(0.1), b2(0.1),   // 隐藏层到输出层的权重和偏置，初始化为0.1learningRate(0.01) {} // 学习率设为0.01// 前向传播函数：计算给定输入x的网络输出double forward(double x) {// 隐藏层计算（没有使用sigmoid激活函数，所以是纯线性变换）hiddenOutput = w1 * x + b1;  // 公式: h = w1*x + b1// 输出层计算（也是线性变换）output = w2 * hiddenOutput + b2; // 公式: y^ = w2*h + b2return output; // 返回预测值}// 计算损失函数（均方误差）double loss(double predicted, double target) {// MSE公式: L = (y^ - y)^2return (predicted - target) * (predicted - target);}// 反向传播函数：计算梯度并更新参数void backward(double x, double predicted, double target) {// 计算预测误差double error = predicted - target; // e = y^ - y// 输出层梯度计算double dL_dw2 = error * hiddenOutput; // ∂L/∂w2 = e * hdouble dL_db2 = error;               // ∂L/∂b2 = e// 隐藏层梯度计算（链式法则）double dL_dhidden = error * w2;      // ∂L/∂h = e * w2double dL_dw1 = dL_dhidden * x;      // ∂L/∂w1 = (e * w2) * xdouble dL_db1 = dL_dhidden;          // ∂L/∂b1 = e * w2// 使用梯度下降更新参数（参数 = 参数 - 学习率 * 梯度）w2 -= learningRate * dL_dw2; // 更新w2b2 -= learningRate * dL_db2; // 更新b2w1 -= learningRate * dL_dw1; // 更新w1b1 -= learningRate * dL_db1; // 更新b1}// 训练一步：执行一次前向传播、损失计算和反向传播void trainStep(double x, double y) {// 1. 前向传播得到预测值double prediction = forward(x);// 2. 计算当前损失double lossValue = loss(prediction, y);// 3. 反向传播更新参数backward(x, prediction, y);// 打印训练信息（调试用）qDebug() << "输入 x =" << x<< "预测值 y^ =" << prediction<< "目标值 y =" << y<< "损失 Loss =" << lossValue;}private:// 网络参数double w1, b1;      // 输入层 -> 隐藏层的权重和偏置double w2, b2;      // 隐藏层 -> 输出层的权重和偏置double learningRate; // 学习率// 缓存前向传播的中间值（用于反向传播）double hiddenOutput; // 隐藏层的输出值double output;       // 网络的最终输出值
};int main(int argc, char *argv[])
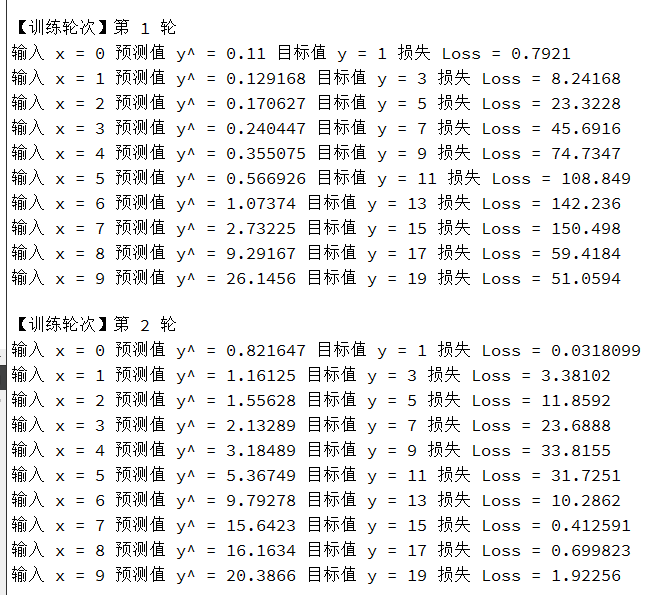
{// 创建神经网络实例SimpleNeuralNetwork net;// 构造训练数据：y = 2x + 1（我们要让网络学习这个线性关系）std::vector<std::pair<double, double>> trainingData;for (double x = 0; x < 10; x += 1) {trainingData.push_back({x, 2 * x + 1}); // 生成(x, y)对}// 多轮训练（epoch指完整遍历数据集一次）for (int epoch = 0; epoch < 1000; ++epoch) {qDebug() << "\n【训练轮次】第" << epoch + 1 << "轮";// 遍历所有训练样本for (const auto& sample : trainingData) {// 对每个样本执行一次训练步骤net.trainStep(sample.first, sample.second);}}// 测试训练好的模型qDebug() << "\n【测试模型】";for (double x = 0; x < 5; ++x) {// 使用训练好的网络进行预测double prediction = net.forward(x);// 打印预测结果和真实值对比qDebug() << "输入 x =" << x<< "预测输出 y^ =" << prediction<< "真实输出 y =" << (2 * x + 1);}
}

前向传播（Forward Propagation）

输入数据通过网络层层计算，得到输出。就是从输入到输出的“推理”过程。

从forward函数可以看出这个神经网络具有：

输入层：1 个神经元，接收输入 x
隐藏层：1 个神经元，使用线性激活（即没有激活函数）
输出层：1 个神经元，输出预测值 y^

损失函数（Loss Function）

衡量预测值与真实值之间的误差。

这里使用的是回归任务中常用的损失函数。

反向传播（Backward Propagation）

根据损失函数的梯度，反向调整网络参数。

实际上训练的结果是得到一组参数，这组参数带入到forward可以对输入内容做出预测。

以下这个版本是计算预测x^2的值， x^2函数图像是非线性的，要加上激活函数：

// Sigmoid 激活函数
double sigmoid(double x) {return 1.0 / (1.0 + exp(-x));
}// Sigmoid 导数（用于反向传播）
double sigmoidDerivative(double x) {double s = sigmoid(x);return s * (1 - s);
}// 改进的神经网络类（支持非线性任务）
class SimpleNeuralNetwork {
public:// 构造函数：初始化网络参数SimpleNeuralNetwork(): w1(0.1), b1(0.1),   // 输入层到隐藏层的权重和偏置w2(0.1), b2(0.1),   // 隐藏层到输出层的权重和偏置learningRate(0.1) {} // 学习率设为0.1（非线性任务需要更大的学习率）// 前向传播函数：计算给定输入x的网络输出（现在使用激活函数）double forward(double x) {// 隐藏层计算（使用sigmoid激活函数）hiddenInput = w1 * x + b1;  // 线性变换hiddenOutput = sigmoid(hiddenInput);  // 非线性激活// 输出层计算（线性变换，不加激活函数以便输出任意值）output = w2 * hiddenOutput + b2;return output; // 返回预测值}// 计算损失函数（均方误差）double loss(double predicted, double target) {return 0.5 * (predicted - target) * (predicted - target); // 乘以0.5方便求导}// 反向传播函数：计算梯度并更新参数（考虑激活函数）void backward(double x, double predicted, double target) {// 计算预测误差double error = predicted - target;// 输出层梯度计算double dL_dw2 = error * hiddenOutput; // ∂L/∂w2 = e * hdouble dL_db2 = error;               // ∂L/∂b2 = e// 隐藏层梯度计算（考虑sigmoid激活函数的导数）double dL_dhidden = error * w2;      // ∂L/∂h = e * w2// 乘以sigmoid的导数double dhidden_dz = sigmoidDerivative(hiddenInput); // ∂h/∂z = h*(1-h)double dL_dz = dL_dhidden * dhidden_dz; // ∂L/∂z = ∂L/∂h * ∂h/∂zdouble dL_dw1 = dL_dz * x;      // ∂L/∂w1 = ∂L/∂z * xdouble dL_db1 = dL_dz;          // ∂L/∂b1 = ∂L/∂z// 使用梯度下降更新参数w2 -= learningRate * dL_dw2;b2 -= learningRate * dL_db2;w1 -= learningRate * dL_dw1;b1 -= learningRate * dL_db1;}// 训练一步：执行一次前向传播、损失计算和反向传播void trainStep(double x, double y) {double prediction = forward(x);double lossValue = loss(prediction, y);backward(x, prediction, y);qDebug() << "输入 x =" << x<< "预测值 y^ =" << prediction<< "目标值 y =" << y<< "损失 Loss =" << lossValue;}void show() {qDebug() << "网络参数:";qDebug() << "w1 = " << w1;qDebug() << "b1 = " << b1;qDebug() << "w2 = " << w2;qDebug() << "b2 = " << b2;}private:// 网络参数double w1, b1;      // 输入层 -> 隐藏层的权重和偏置double w2, b2;      // 隐藏层 -> 输出层的权重和偏置double learningRate; // 学习率// 缓存前向传播的中间值（用于反向传播）double hiddenInput;  // 隐藏层的输入值（激活函数之前）double hiddenOutput; // 隐藏层的输出值（激活函数之后）double output;       // 网络的最终输出值
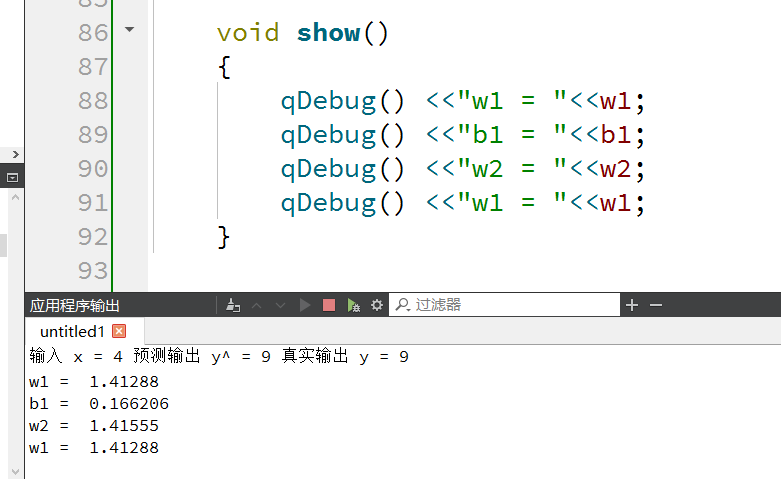
};int main(int argc, char *argv[]) {// 创建神经网络实例SimpleNeuralNetwork net;// 构造非线性训练数据：y = x^2（我们要让网络学习这个非线性关系）std::vector<std::pair<double, double>> trainingData;for (double x = -2.0; x <= 2.0; x += 0.2) {trainingData.push_back({x, x * x}); // 生成(x, x^2)对}// 多轮训练for (int epoch = 0; epoch < 1000; ++epoch) {qDebug() << "\n【训练轮次】第" << epoch + 1 << "轮";// 遍历所有训练样本for (const auto& sample : trainingData) {net.trainStep(sample.first, sample.second);}}// 测试训练好的模型qDebug() << "\n【测试模型】";for (double x = -2.0; x <= 2.0; x += 0.5) {double prediction = net.forward(x);qDebug() << "输入 x =" << x<< "预测输出 y^ =" << prediction<< "真实输出 y =" << (x * x)<< "误差 =" << (prediction - x * x);}net.show();
}