Leetcode 494. 目标和
Leetcode 494. 目标和
回溯算法
回溯算法实现,但会出现 超时 的情况。时间复杂度是O(2^n), n表示数组的长度,每个数字有两个状态,因此是2^n。
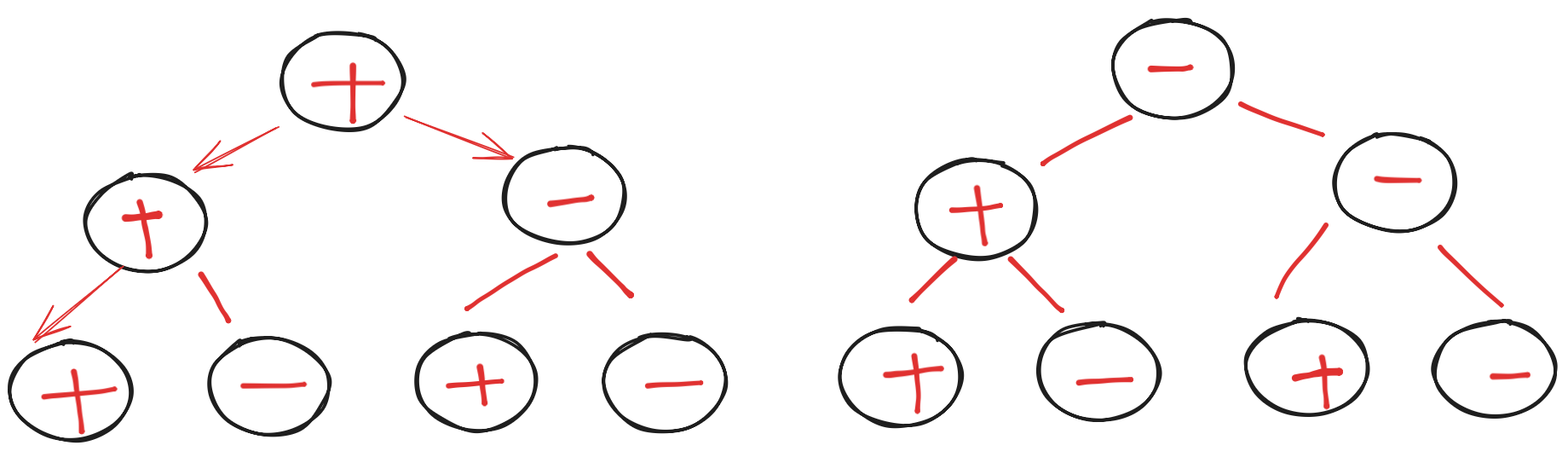
思路就是构建一个决策树,如下图所示:
- 决策树构建:每个数字有两种选择(加或减),形成一个二叉树
- 递归探索:深度优先遍历所有可能的组合
- 终止条件:当处理完所有数字时,检查当前和是否等于target
- 剪枝优化:可以提前终止不可能达到target的分支
Code
class Solution(object):def findTargetSumWays(self, nums, target):""":type nums: List[int]:type target: int:rtype: int"""# @lc code=endself.count = 0self.backtracking(nums, target, 0, 0)return self.countdef backtracking(self, nums, target, index, cur_sum):if index == len(nums):if cur_sum == target: ### 串联起所有整数,所以是放到这里面来进行退出self.count += 1return self.backtracking(nums, target, index+1, cur_sum + nums[index])self.backtracking(nums, target, index+1, cur_sum - nums[index])
动规算法
思路:
- 这道题是关键是要将带“+”和“-”的数字进行划分,根据这二者的关系得到一个方程组,根据方程组来得到一个关系
- 假设left为带“+”的数字总和,right为带"-"的数字总和。(这里的数字都是大于等于0,正负性是由前面的符号决定的,这里是将去除符号后得到的数字)
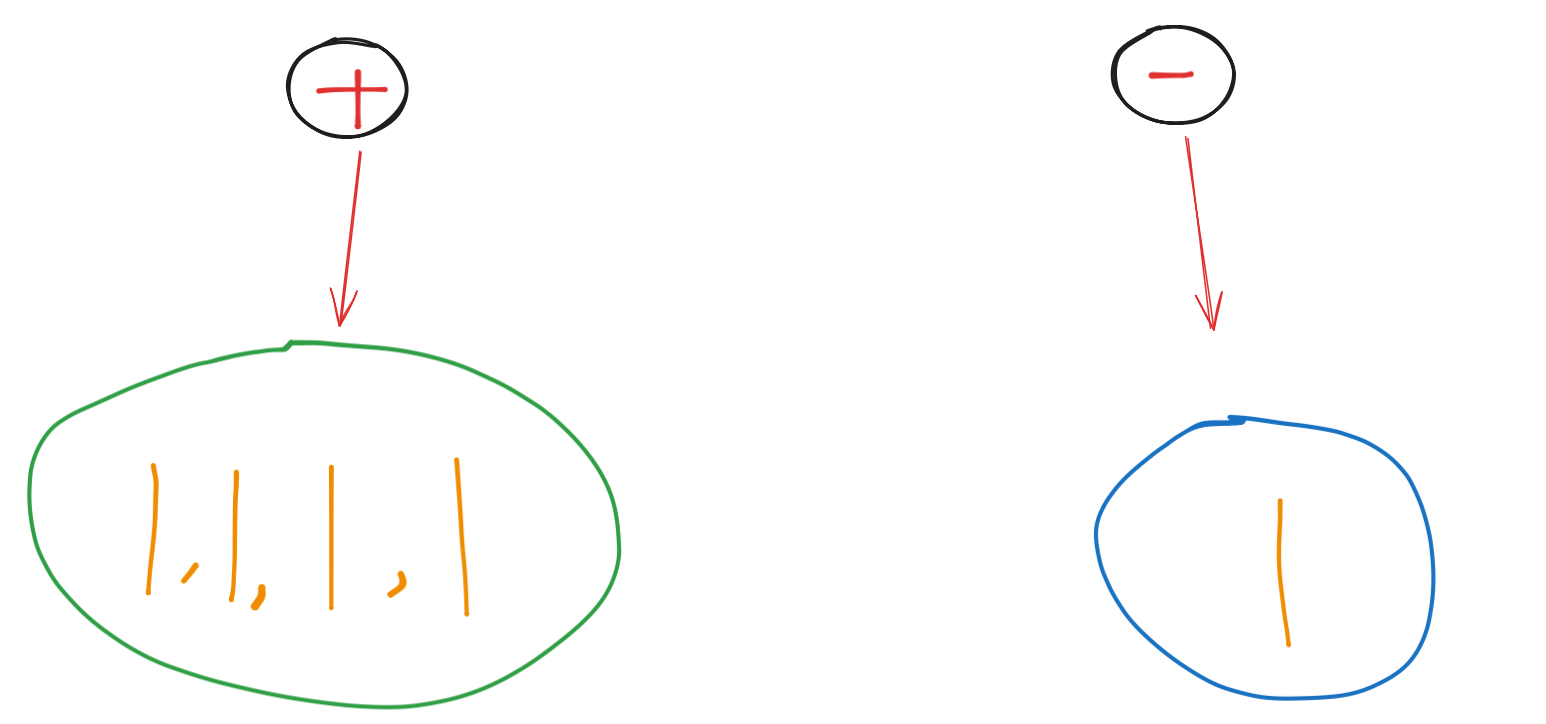
- 另外,为什么left + right == sums,是因为题目已经限制了 nums[i] >= 0,因此原数组的每一个数字都是正的
- 那么有left + right == sums. left - right == target,结合二者得到 left = ( target + sums ) / 2
- 因此就将关系转换到只要求背包容量为 left == ( target + sums ) /2 下有多少种这样的组合。
- 另外,若 nums = [1,1,1,1,1,1,1], target = 4, sums = 7 , 此时 ( target + sums ) /2 = 5.5, 那此时就说明了不存在这样的组合来满足题意,因为都是nums里都是整数。
- 那关系就很清楚了,我们现在只要对数组进行求和,来判断和为 ( target + sums ) /2 下的组合有多少种就行。
- 求和为某个target下的组合,回溯可以解决。
- 这道题的dp数组的实现方式就跟“爬楼梯”差不多了,但爬楼梯限定在了距离为1和2,这里的话是根据nums[i]的值
Code
class Solution(object):def findTargetSumWays(self, nums, target):""":type nums: List[int]:type target: int:rtype: int"""### 1. dp数组定义,一维数组,dp[j]表示凑成 left==j 下的组合次数nums_sum = sum(nums)left = (nums_sum + target) // 2 ### 向下取整,转换为int类型if (nums_sum + target) % 2 == 1:return 0if abs(target) > nums_sum:return 0## 1. dp数组定义# dp = [0] * ( nums_sum + 1 ) ### 数组存在多余的部分,直接到left就行了dp = [0] * ( left + 1 )### 2. dp初始化。dp[0] = 1 ### 3. 递推公式. ### dp[j] += dp[j-nums[i]]### 4. 遍历顺序### 外层从小到大,内层从大到小(表示一个物品只取一次)for i in range(len(nums)):for j in range(len(dp)-1, -1, -1):if j >= nums[i]: ### 涉及到数组下标的有效值,因此要做判断。当然这个判断也可以嵌入到循环中,这样的话可以节省循环的次数,不过为了逻辑清晰性,这样也行dp[j] += dp[j-nums[i]] ### 爬楼梯的话 nums = [1,2]### 5. 打印dp数组return dp[left] 