傅里叶与相位偏移
一、简介
大三的《离散数学》。。。。。

傅里叶变换是数学与工程领域的一项革命性工具,其核心思想是将复杂信号分解为简单正弦波的叠加,实现从时域(时间维度)到频域(频率维度)的转换。通过这种变换,可以分析信号的频率成分,广泛应用于信号处理、通信、图像分析、物理等领域
相位我们一般称之为相位偏移,在编码信息(通信)、控制波传播方向(雷达)、保持信号完整性(滤波)、重建结构(成像)等领域有非常重要的作用。
二、傅里叶变换简介
傅里叶级数
傅里叶变换 - crossoverpptx - 博客园


https://zhuanlan.zhihu.com/p/41455378
核心思想
分解与合成
-
分解与合成
任何复杂信号(如音频、图像、电磁波)均可表示为不同频率、幅度和相位的正弦波(或复指数函数)的组合。-
时域:信号随时间变化的波形(如心电图、音乐波形)。
-
频域:信号中各频率分量的强度与相位分布(如频谱图)。
-
-
时频转换的意义
-
分析:识别信号中的主要频率成分(如检测噪声、识别语音特征)。
-
处理:在频域完成滤波、压缩等操作后,再通过逆变换还原信号。
-
数学表达
主要类型
-
信号滤波
-
去除噪声(如消除音频中的杂音),保留特定频率成分。
-
-
图像压缩
-
JPEG 格式通过傅里叶变换分离高频(细节)和低频(轮廓),压缩高频数据。
-
-
通信系统
-
调制解调(如WiFi、5G)利用频域分配传输多路信号。
-
-
物理学
-
量子力学中波函数的频域分析,光学中的衍射计算。
-
时域频域的互换
时域(Time Domain)
-
定义:信号随时间变化的表示形式,横轴为时间,纵轴为幅值。
-
示例:音频波形、心电图、股票价格曲线。
-
特点:直观展示信号的动态变化,但难以直接识别频率特性。

频域(Frequency Domain)
-
定义:信号在频率维度上的表示形式,横轴为频率,纵轴为幅值或相位。
-
示例:频谱图(显示各频率分量的强度)、音乐的音符分布。
-
特点:清晰展示信号的频率组成,便于分析周期性、噪声或谐波。
-

转换原理


数学工具:傅里叶变换

1、连续傅里叶

2、 离散傅里叶

二维:

转换方法

三、相位与相位偏移
相位:
周期性波形的波粒的位置称为波形的“相位”。一个波形的一个完整周期的完整相位是360°
相位差
正弦波的相位差可以定义为“一个波领先或落后于另一波的时间间隔”
相位差不是一个波的特性,而是两个或多个波的相对特性。这也称为“相位角”或“相位偏移”。

相位差方程
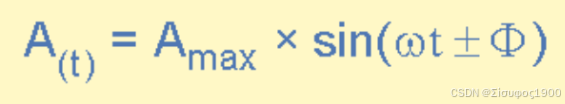

相位差和相移理论知识概括-CSDN博客
 四步相移法
四步相移法
四步相移法(Four-Step Phase-Shifting Method) 是一种通过采集多幅相位差已知的干涉图来解调相位信息的技术,广泛应用于光学干涉测量、结构光三维成像、表面形貌检测等领域。其核心思想是通过引入已知的相位偏移,利用数学公式消除背景光强和调制幅度的干扰,从而精确提取目标相位。
基本原理
 四步相移法的具体步骤
四步相移法的具体步骤
案例:
【四步相移法】光强公式理解和两个问题梳理_4部相位法-CSDN博客
1、先移动一个90度

2、根据1的推导 分别移动2 步、3步、4步
3、如何确定相位值:

应用场景
-
光学干涉测量
检测光学元件表面面形、薄膜厚度。 -
结构光三维成像
投射四步相移条纹,解调物体表面三维形貌(如人脸扫描、工业检测)。 -
数字全息术
重建物光波的复振幅分布。 -
振动分析
测量机械部件的微振动相位变化。
与其他相移法的对比

示例:结构光三维成像
-
投射四步相移正弦条纹:
-
投影仪依次投射相位差为 π/2π/2 的条纹图案。
-
-
相机采集变形条纹:
-
物体表面形貌导致条纹相位调制。
-
-
计算相位:
-
使用四步相移公式解算包裹相位。
-
-
相位解包裹与三维重建:
-
结合标定参数,将相位转换为三维坐标
-
Matlab测试;
% 功能:模拟生成四步相移条纹图,解算相位并解包裹clc; clear; close all;%% 参数设置
N = 512; % 图像尺寸(N×N像素)
fringe_freq = 20; % 条纹频率(单位:周期/图像宽度)
noise_level = 0.1; % 噪声水平(0~1)%% 1. 生成模拟的四步相移条纹图
[x, y] = meshgrid(1:N, 1:N);
phi_true = 2*pi*fringe_freq*(x/N + y/N); % 真实相位(模拟平面倾斜)
phi_wrapped = angle(exp(1i*phi_true)); % 包裹相位(-π到π)% 生成四步相移条纹图(I1-I4)
I1 = 128 + 127*cos(phi_wrapped + 0); % 相位偏移 0
I2 = 128 + 127*cos(phi_wrapped + pi/2); % 相位偏移 π/2
I3 = 128 + 127*cos(phi_wrapped + pi); % 相位偏移 π
I4 = 128 + 127*cos(phi_wrapped + 3*pi/2); % 相位偏移 3π/2% 添加噪声模拟实际采集环境
I1 = imnoise(uint8(I1), 'gaussian', 0, noise_level);
I2 = imnoise(uint8(I2), 'gaussian', 0, noise_level);
I3 = imnoise(uint8(I3), 'gaussian', 0, noise_level);
I4 = imnoise(uint8(I4), 'gaussian', 0, noise_level);%% 2. 四步相移法解算包裹相位
I1 = double(I1); I2 = double(I2); I3 = double(I3); I4 = double(I4);% 相位解算公式
phi_wrapped_calculated = atan2((I4 - I2), (I1 - I3));%% 3. 相位解包裹(使用MATLAB内置函数)
phi_unwrapped = unwrap(phi_wrapped_calculated, [], 2); % 水平方向解包裹
phi_unwrapped = unwrap(phi_unwrapped, [], 1); % 垂直方向解包裹%% 4. 结果可视化
figure('Color', 'white');% 原始干涉图(以I1为例)
subplot(2,2,1); imshow(uint8(I1), []);
title('相移条纹图 (I1, 0°)'); axis off;% 包裹相位
subplot(2,2,2); imagesc(phi_wrapped_calculated);
colormap jet; colorbar; title('解算的包裹相位'); axis off;% 解包裹后的相位
subplot(2,2,3); imagesc(phi_unwrapped);
colormap jet; colorbar; title('解包裹后的连续相位'); axis off;% 真实相位(对比)
subplot(2,2,4); imagesc(phi_true);
colormap jet; colorbar; title('真实相位(参考)'); axis off;%% 5. 误差分析(可选)
error = phi_unwrapped - phi_true;
figure; imagesc(error);
colormap jet; colorbar; title('相位解算误差'); axis off;
fprintf('最大误差: %.4f rad\n均方根误差: %.4f rad\n', ...max(abs(error(:))), sqrt(mean(error(:).^2)));




