Python实现点云投影到直线、平面、柱面和球面
本节我们分享点云的投影计算,按直线 → 平面 → 圆柱 → 球面顺序介绍。其实无论投影到哪种几何基元,都遵循“三步走”:① 读取或生成点云 → ② 计算每个点在目标几何体上的最近点 → ③ 用最近点坐标替换原坐标并可视化。
下面分别给出四种算法的具体做法。
1、投影到直线
目标
把点云P = {pᵢ}压到一条无限长直线上,得到新的点云P′ = {p′ᵢ},其中p′ᵢ是pᵢ到直线的正交投影。输入
直线方向向量
d(单位化)直线上任意一点
o算法
读取点云
P。对每个点
pᵢ计算参数tᵢ = (pᵢ − o)·d。投影点
。= o + tᵢ d
用
更新P。使用 Open3D 的
draw_geometries可视化。
2、投影到平面
目标
将P正交投影到给定平面。输入
平面法向量
n(单位化)平面上任意一点
o算法
读取点云
P。对每个点
pᵢ计算有符号距离dᵢ = (pᵢ − o)·n。投影点
。= pᵢ − dᵢ n
用
更新P。可视化。
3、投影到圆柱面
目标
把P投影到半径为r、轴线已知的圆柱面上。输入
圆柱轴线方向向量
d(单位化)轴线上任意一点
o半径
r算法
读取点云
P。对每个点
pᵢ:
① 计算到轴线的最近点qᵢ = o + ((pᵢ − o)·d) d;
② 计算离轴距离向量vᵢ = pᵢ − qᵢ;
③ 归一化uᵢ = vᵢ / ‖vᵢ‖(若‖vᵢ‖ = 0可任取正交于d的单位向量);
④ 圆柱表面点。= qᵢ + r uᵢ
用
更新P。可视化。
4、投影到球面
目标
把P投影到以c为中心、半径R的球面上。输入
球心
c半径
R算法
读取点云
P。对每个点
pᵢ:
① 计算方向向量vᵢ = pᵢ − c;
② 归一化uᵢ = vᵢ / ‖vᵢ‖;
③ 球面点p′ᵢ = c + R uᵢ。用
p′ᵢ更新P。可视化。
当然,本次使用的数据依然是兔砸,闪亮登场:
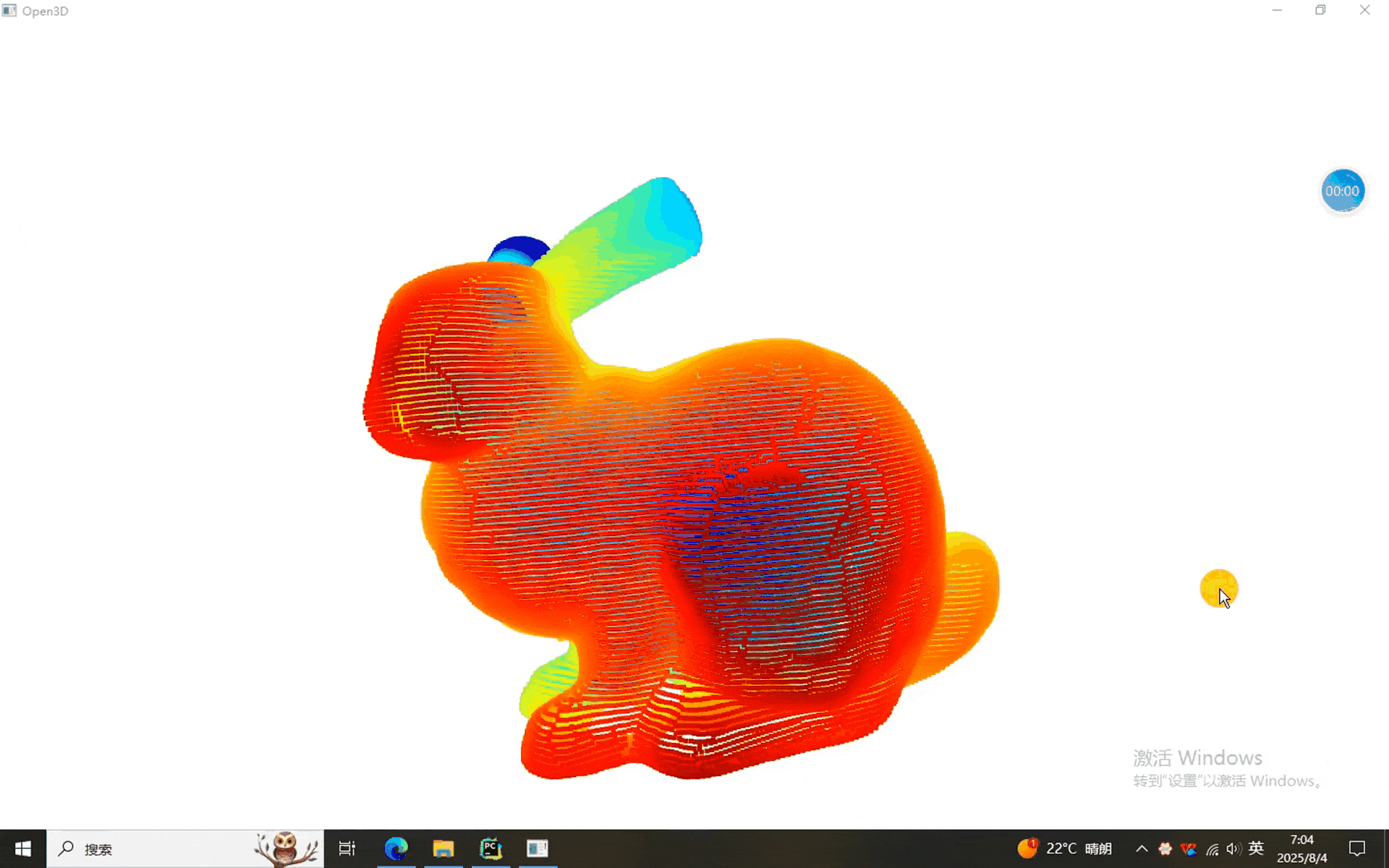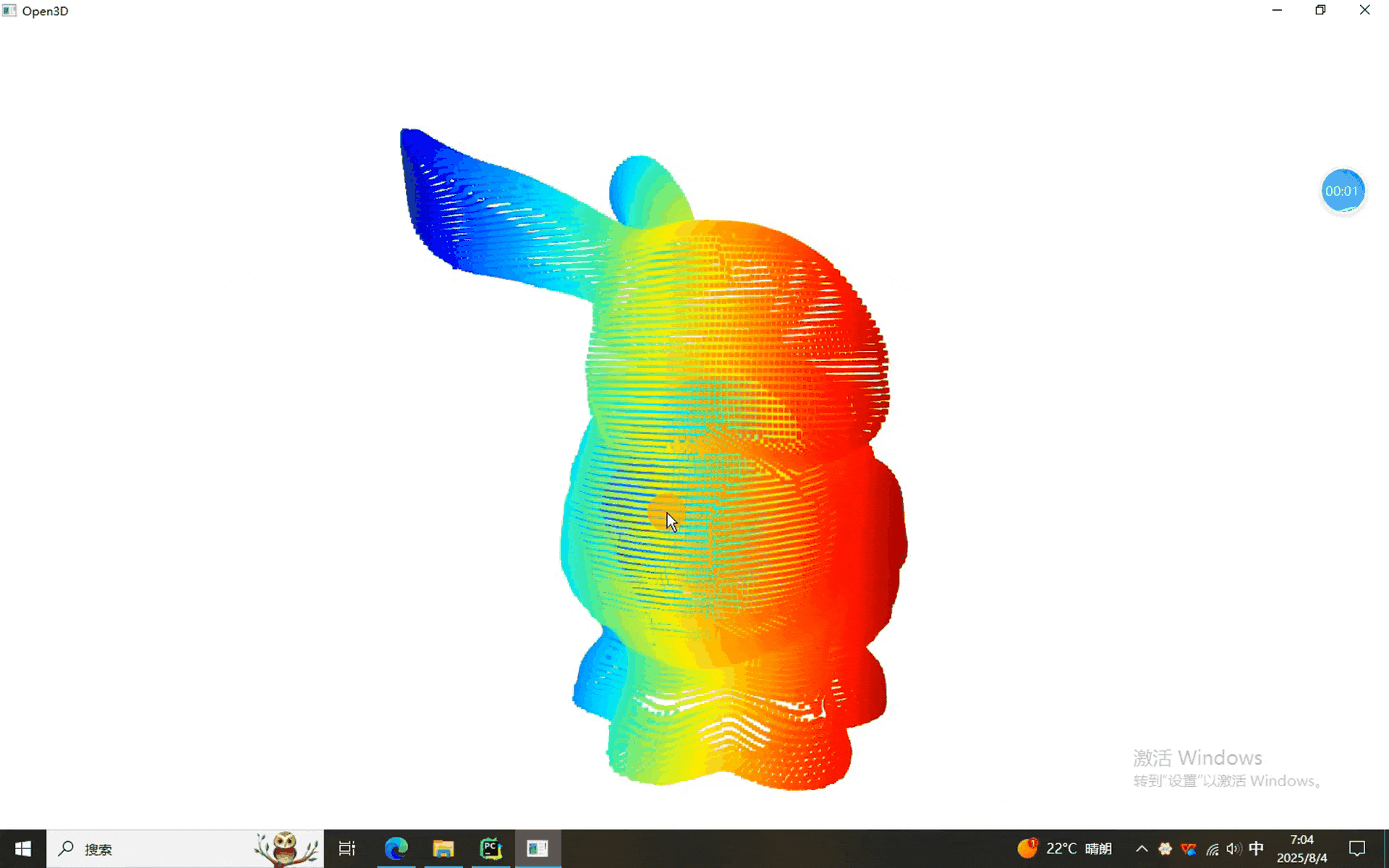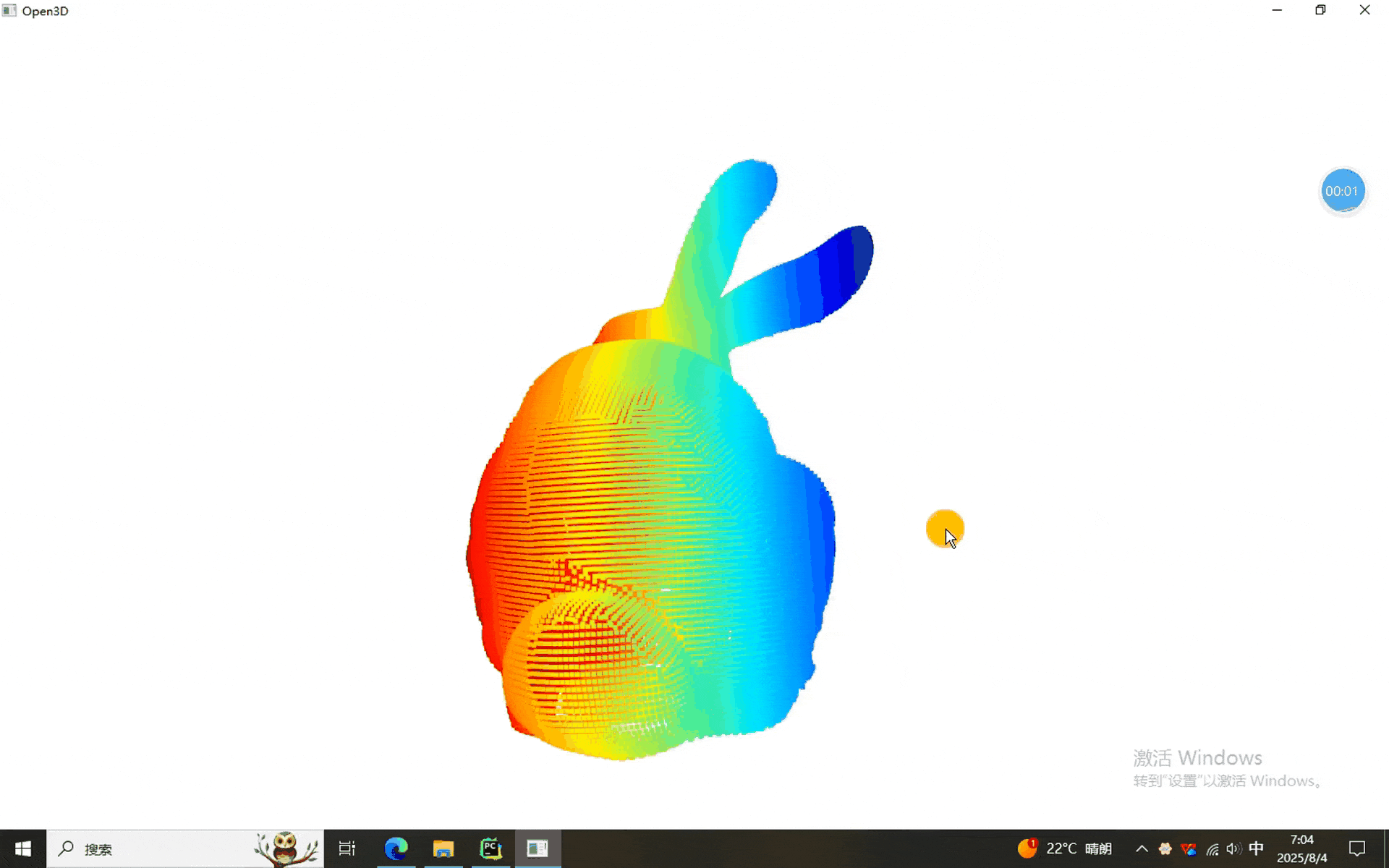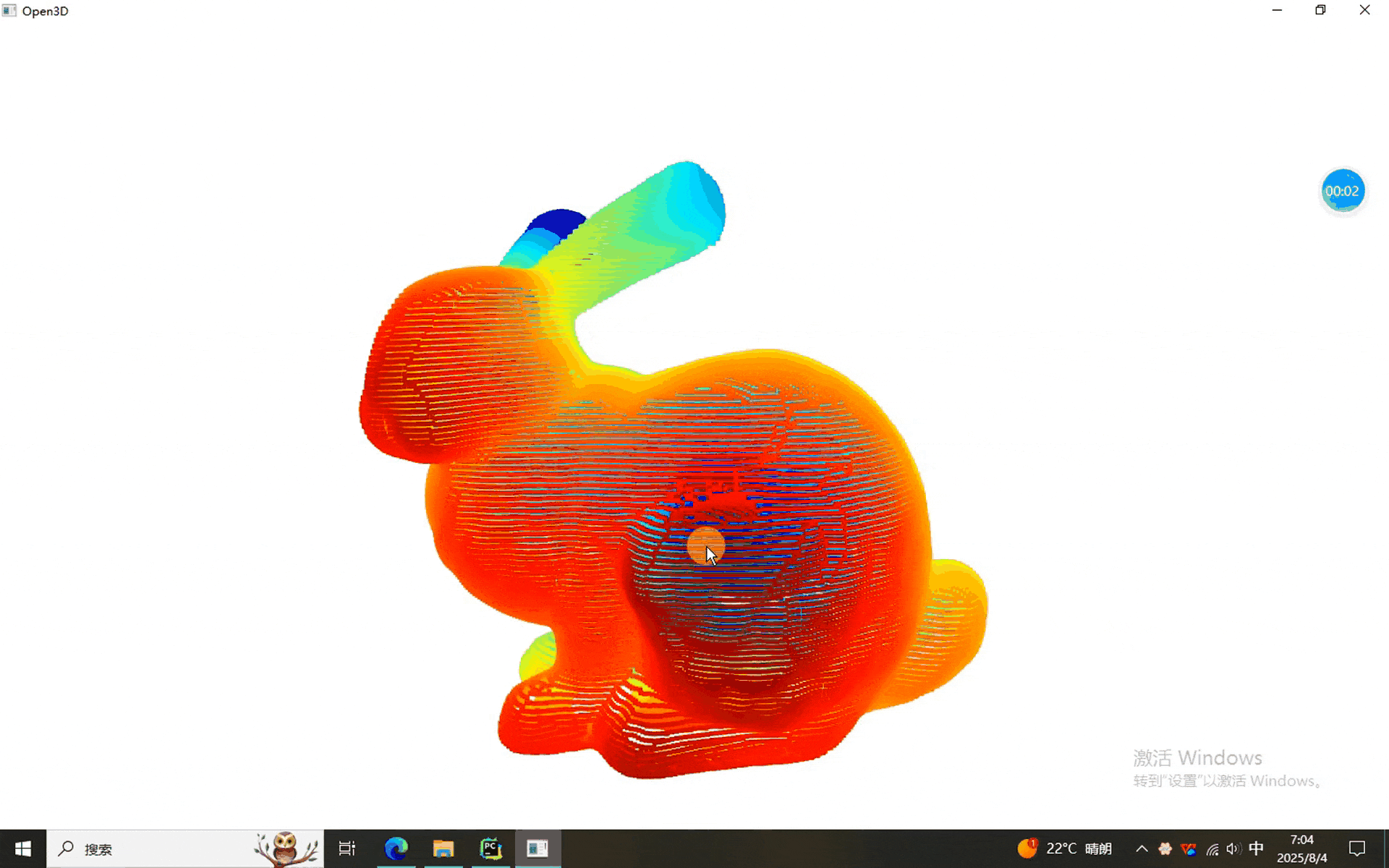
一、四种投影程序
import open3d as o3d
import numpy as np
import os# -------------------------------------------------
# 基础工具
# -------------------------------------------------
def load_pcd(name):pcd = o3d.io.read_point_cloud(name)if pcd.is_empty():raise RuntimeError(f"找不到或无法读取 {name}")return pcddef save_pcd(pcd, src_name, suffix):out = src_name.replace(".pcd", f"_proj_{suffix}.pcd")o3d.io.write_point_cloud(out, pcd, print_progress=False)print(f"已保存:{out}")def view(pcd, title):o3d.visualization.draw_geometries([pcd], window_name=title, width=900, height=700, left=50, top=50)# -------------------------------------------------
# 四种投影实现
# -------------------------------------------------
def proj_line(pcd, line_p, line_d):pts = np.asarray(pcd.points)d = line_d / np.linalg.norm(line_d)t = ((pts - line_p) @ d)[:, None]proj = line_p + t * dnew = o3d.geometry.PointCloud(o3d.utility.Vector3dVector(proj))if pcd.has_colors():new.colors = pcd.colorsreturn newdef proj_plane(pcd, coeffs):A, B, C, D = coeffsn = np.array([A, B, C], dtype=float)n = n / np.linalg.norm(n)pts = np.asarray(pcd.points)dist = (pts @ n + D)[:, None]proj = pts - dist * nnew = o3d.geometry.PointCloud(o3d.utility.Vector3dVector(proj))if pcd.has_colors():new.colors = pcd.colorsreturn newdef proj_cylinder(pcd, axis_p, axis_d, radius):pts = np.asarray(pcd.points)d = axis_d / np.linalg.norm(axis_d)vec = pts - axis_pt = (vec @ d)[:, None]axis_proj = axis_p + t * dradial = pts - axis_projnorms = np.linalg.norm(radial, axis=1, keepdims=True)norms[norms == 0] = 1surf = axis_proj + radius * radial / normsnew = o3d.geometry.PointCloud(o3d.utility.Vector3dVector(surf))if pcd.has_colors():new.colors = pcd.colorsreturn newdef proj_sphere(pcd, center, radius):pts = np.asarray(pcd.points)vec = pts - centernorms = np.linalg.norm(vec, axis=1, keepdims=True)norms[norms == 0] = 1surf = center + radius * vec / normsnew = o3d.geometry.PointCloud(o3d.utility.Vector3dVector(surf))if pcd.has_colors():new.colors = pcd.colorsreturn new# -------------------------------------------------
# 主流程
# -------------------------------------------------
def main():src_file = "E:/CSDN/规则点云/bunny.pcd"if not os.path.isfile(src_file):print("请确保点云存在!")returnpcd = load_pcd(src_file)print(f"已加载 {src_file},共 {len(pcd.points)} 点")# 1) 直线line_p = np.array([0., 0., 0.])line_d = np.array([1., 1., 1.])line_proj = proj_line(pcd, line_p, line_d)# save_pcd(line_proj, src_file, "line")view(line_proj, "投影到直线")# 2) 平面(示例:x+2y+3z+4=0)plane_coeff = [1, 2, 3, 4]plane_proj = proj_plane(pcd, plane_coeff)# save_pcd(plane_proj, src_file, "plane")view(plane_proj, "投影到平面")# 3) 圆柱(Z轴,半径 2.5)axis_p = np.array([0., 0., 0.])axis_d = np.array([0., 0., 1.])radius = 2.5cyl_proj = proj_cylinder(pcd, axis_p, axis_d, radius)# save_pcd(cyl_proj, src_file, "cylinder")view(cyl_proj, "投影到圆柱")# 4) 球(原点,半径 1)center = np.array([0., 0., 0.])sphere_r = 1.0sphere_proj = proj_sphere(pcd, center, sphere_r)# save_pcd(sphere_proj, src_file, "sphere")view(sphere_proj, "投影到球面")print("全部完成!")if __name__ == "__main__":main()
二、四种投影结果
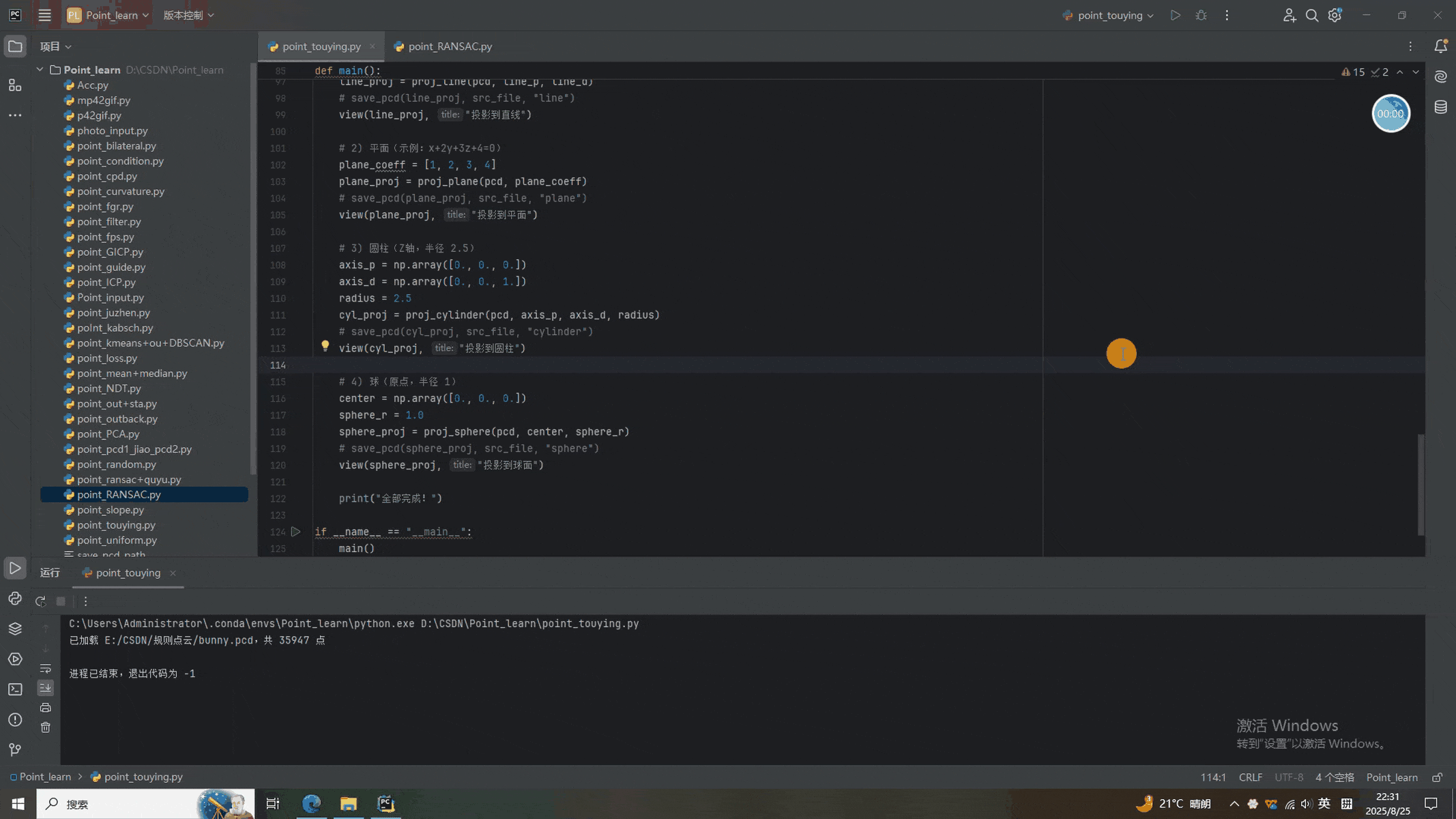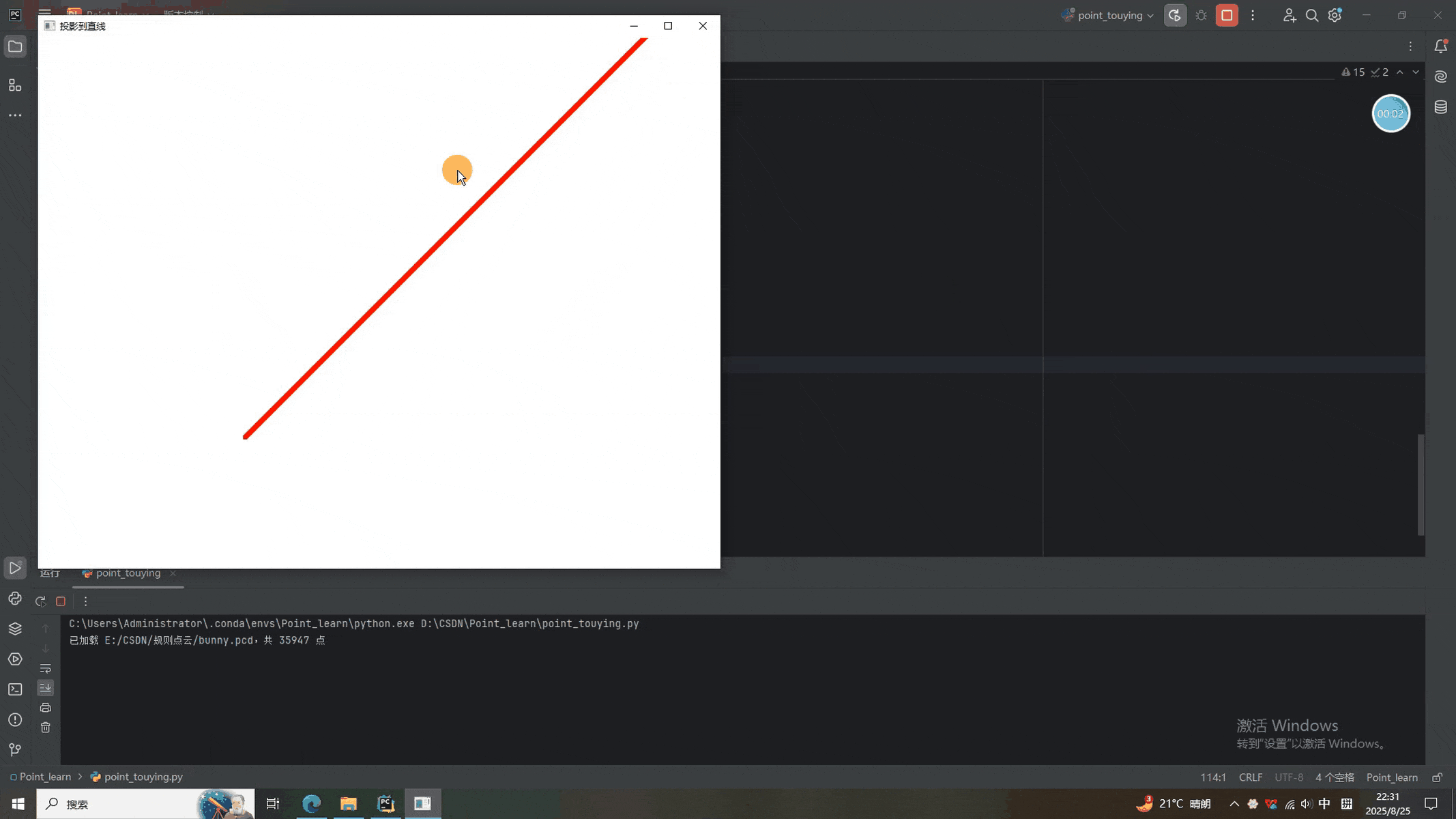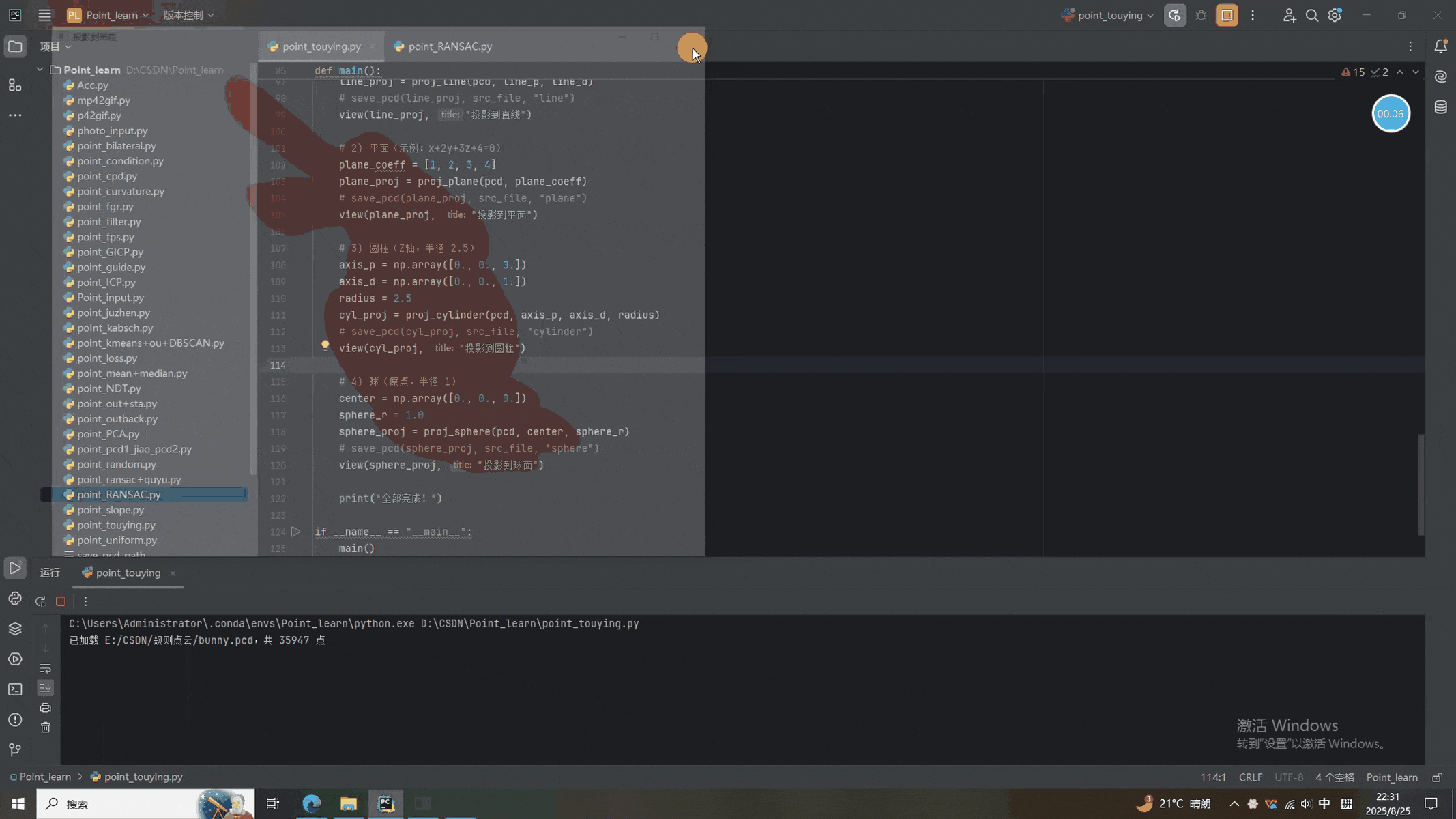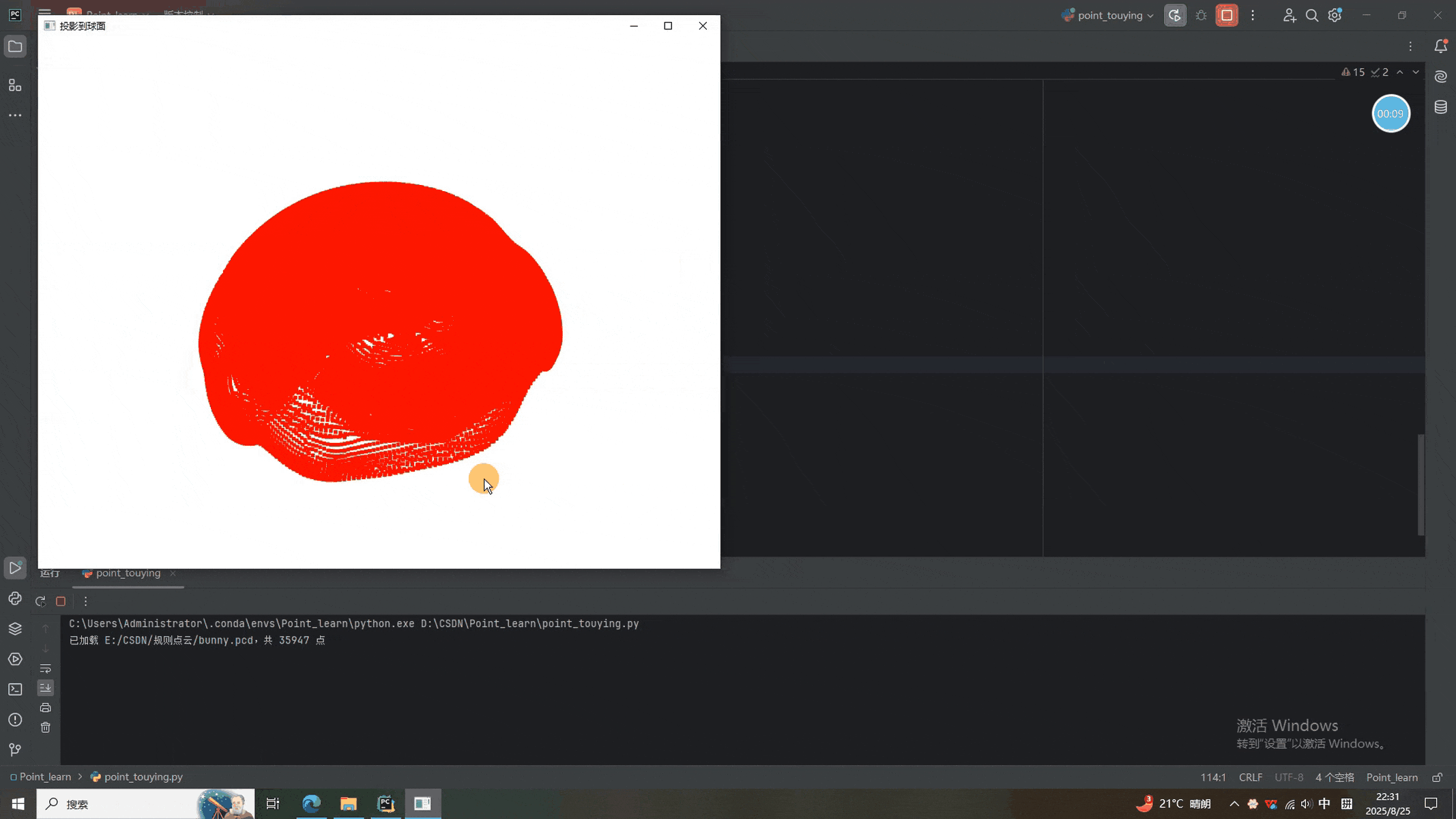
可以看到,兔砸分别被投影到了直线、平面、圆柱和球面上。当然,根据参数的不同,最后显示的不同,有兴趣的同学可以调节参数试一试。
就酱,下次见^-^
