洛谷B3836 [GESP202303 二级] 百鸡问题
题目描述
“百鸡问题”是出自我国古代《张丘建算经》的著名数学问题。大意为:
“每只公鸡 5 元,每只母鸡 3 元,每 3 只小鸡 1 元;现在有 100 元,买了 100 只鸡,共有多少种方案?”
小明很喜欢这个故事,他决定对这个问题进行扩展,并使用编程解决:如果每只公鸡 x 元,每只母鸡 y 元,每 z 只小鸡 1 元;现在有 n 元,买了 m 只鸡,共有多少种方案?
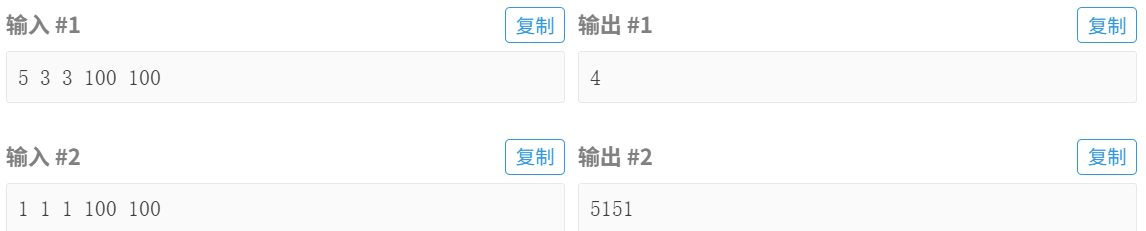
输入格式
输入一行,包含五个整数,分别为问题描述中的 x,y,z,n,m。约定 1≤x,y,z≤10,1≤n,m≤1000。
输出格式
输出一行,包含一个整数 C,表示有 C 种方案。
说明/提示
【样例 1 解释】
这就是问题描述中的“百鸡问题”。4 种方案分别为:
- 公鸡 0 只、母鸡 25 只、小鸡 75 只。
- 公鸡 4 只、母鸡 18 只、小鸡 78 只。
- 公鸡 8 只、母鸡 11 只、小鸡 81 只。
- 公鸡 12 只、母鸡 4 只、小鸡 84 只。
GESP二级编程考试重点考察的是字符和嵌套循环的编程能力。因此对于嵌套循环类题目,考生必须具备暴力枚举和枚举优化能力,暴力能够拿部分分,只有优化才能拿满分,因此要求练习时先写出纯暴力枚举代码,再逐步优化。只有进行优化循环次数和优化循环层数的大量练习,才能确保顺利通过GESP二级考试。
枚举算法两大特点:①解的有限性、②解的可判定性。枚举问题所有可能的解必须是有限个,且能在合理时间内列举完,如果解是无限的(比如实数范围内的解),枚举将无法终止;如果无法判定某个候选解是否正确,枚举就失去意义,判定过程必须明确无歧义。
1、初步无脑思路:暴力枚举
这种无脑思路,就是将每一种买鸡的情况罗列出来,由计算机来检查是否符合题目的要求,所谓题目要求就是等量关系:钱等量关系是100钱,鸡的等量关系也是100只。
其实小学生都学过枚举思维了,只不过这次需要让计算机代替人去做,这是计算机最擅长做的事情。越往高级别学习,尤其到了算法阶段的学习,本质上都是让计算机更加聪明的执行枚举过程。好的我们来分析题目吧!
题目中描述的公鸡、母鸡、小鸡三种物品,因此我们需要三层嵌套循环来实现题目的暴力枚举,假设公鸡i只,母鸡j只,小鸡k只,可以得到如下等式关系:
百钱关系:5i+3j+k/3=100钱,隐含关系:小鸡只数为3的倍数;
百鸡关系:i+j+k=100只。
根据以上等式关系,通过暴力枚举公鸡、母鸡、小鸡的只数范围(0~100)进行解题。
#include <bits/stdc++.h>
using namespace std;
int main(){for(int i = 0; i <= 100; i++){for(int j = 0; j <= 100; j++){for(int k = 0; k <= 100; k+=3){// 只数等量 钱数等量if(i+j+k==100 && 5*i+3*j+k/3 == 100){cout << "公鸡" << i << " 母鸡" << j << " 小鸡" << k << endl;}}}}return 0;
}2、枚举次数优化
我们对于枚举,可以进行优化,而不是像上面那样无脑循环遍历与枚举!首先思考减少枚举数据的范围。对于本题我们不难发现,公鸡和母鸡的数目不用从0枚举到100,买到的公鸡在达到20只时,就已经达到了预期的100钱。同理母鸡只数最多到33只,因此我们修改程序,将循环的范围缩小。
#include <bits/stdc++.h>
using namespace std;
int main(){for(int i = 0; i<=20; i++){for(int j = 0; j<=33; j++){for(int k = 0; k <= 100; k+=3){// 只数等量 钱数等量if(i+j+k==100 && 5*i+3*j+k/3 == 100){cout << "公鸡" << i << " 母鸡" << j << " 小鸡" << k << endl;}}}}return 0;
}3、clock()函数的使用
为了体验优化的效果,将百钱百鸡改为万钱万鸡,同时在程序中加入clock()函数,以此检查程序运行的速度是否变快。
#include <bits/stdc++.h>
using namespace std;
int main(){for(int i=0; i<=10000/5; i++){for(int j=0; j<=10000/3; j++){for(int k=0; k<=10000; k+=3){// 只数等量 钱数等量if(i+j+k==10000 && 5*i+3*j+k/3 == 10000){cout << "公鸡" << i << " 母鸡" << j << " 小鸡" << k << endl;}}}}cout << "耗时: " << ((double)clock() / CLOCKS_PER_SEC) << " 秒";return 0;
}clock() 是 C/C++ <ctime>(或 <time.h>)里的一个函数,用来测量进程从启动到当前时刻所用的 CPU 时钟数。把它换算成“秒”就可以得到运行时间。
(1)原型与返回值
#include <ctime> // 或 <time.h>
clock_t clock(void);
- 返回类型:clock_t(通常是 long)。
- 单位:CPU 时钟“滴答”(ticks)。
- 宏 CLOCKS_PER_SEC 表示 1 秒包含多少 ticks(Linux/Windows 下通常是 1000000)。
(2)在代码里的三步用法
a)开始计时
代码并没有显式保存开始时刻,因为三重循环一开始就执行,所以把clock() 放在循环结束后即可测得总耗时。
b) 结束计时
double elapsed = (double)clock() / CLOCKS_PER_SEC;
先把 clock_t 强制转换成 double,再除以 CLOCKS_PER_SEC,得到 秒数。因为除法需要小数精度,而 clock_t 本质是整型(long),如果不转 double,clock() / CLOCKS_PER_SEC 会先做整数除法,结果把小数部分直接截断为 0,导致永远得到 0 秒。
强制转换成 double 后,整个表达式变为 浮点除法,才能保留毫秒级的小数部分。
(3)输出
cout << "耗时: " << elapsed << " 秒";
(4)常见注意点:
- 单位混淆 :忘记除以 CLOCKS_PER_SEC,直接输出会是一串大数字。
- 精度:Windows 下 clock() 精度约 1 ms;Linux 下可用 clock_gettime 更高精度。
- 多线程:clock() 统计的是进程CPU 时间,不包括阻塞 I/O;多线程场景可用 std::chrono。
(5)一句话总结
clock() 就是“秒表”:
开始 → 结束 → (结束-开始)/CLOCKS_PER_SEC 得到秒数。
4、优化枚举次数对比
对于万钱买万鸡的情况,上面两种枚举分别花的时间如下:
无脑暴力:
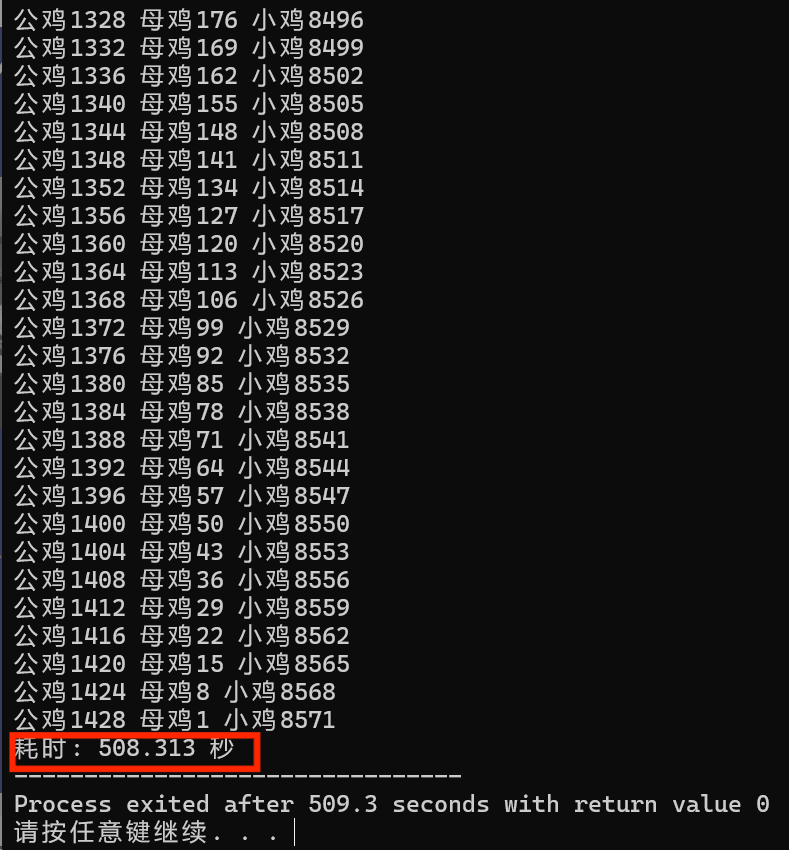
枚举次数优化后
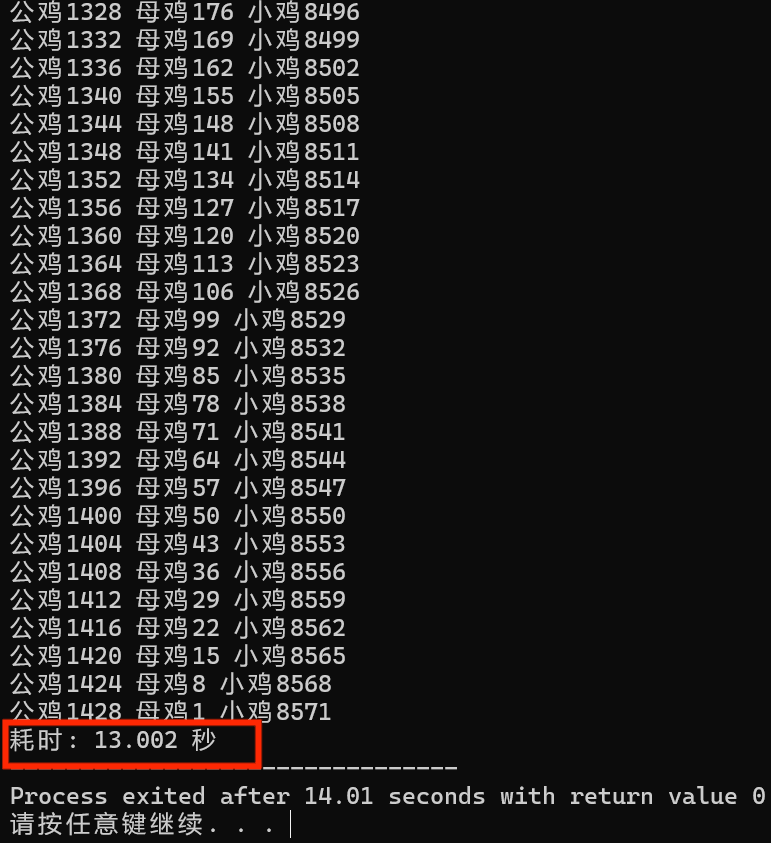
我们发现:数量到达一定级别后,优化枚举次数效果非常明显,执行时间由原来的508多秒到优化后的13秒多。但是执行时间还是不可接受!!!
5、枚举层数优化
我们i,j枚举时,先确定公鸡和母鸡的个数,然后剩下的钱全部用来买小鸡,小鸡数k=10000-i-j,我们只需要判断小鸡数是3的倍数,且花掉的钱数正好是10000钱即可!
#include <bits/stdc++.h>
using namespace std;
int main(){for(int i=0; i<=10000/5; i++){for(int j=0; j<=10000/3; j++){int k=10000-i-j;// 只数等量if(k%3) continue;// 钱数等量if(5*i+3*j+k/3 == 10000){cout << "公鸡" << i << " 母鸡" << j << " 小鸡" << k << endl;}}}cout << "耗时: " << ((double)clock() / CLOCKS_PER_SEC) << " 秒";return 0;
}我们发现运行时间差距巨大,优化循环层数的执行时间居然差不多是150毫秒,根本不是一个数量级!
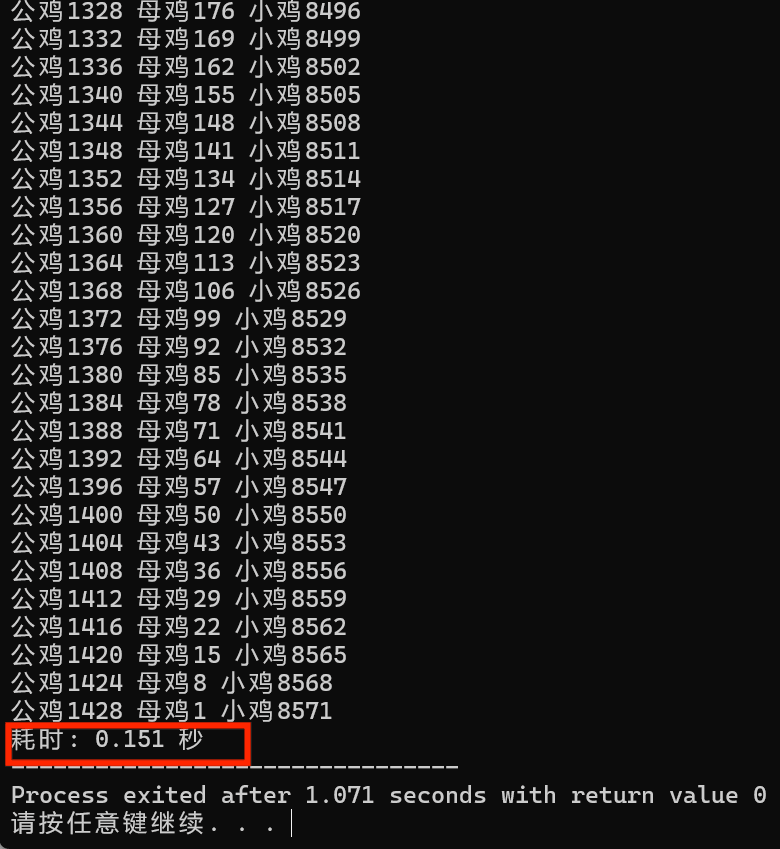
所以最后结论就是循环层数越少越好,专业一点说法就是:嵌套循环层数越少越好,当暴力枚举消耗时间太多,首先要想到优化循环层数,其次想办法优化循环次数。
6、代码(每只公鸡 x 元,每只母鸡 y 元,每 z 只小鸡 1 元;现在有 n 元,买了 m 只鸡)
#include <iostream>
using namespace std;int main() {int x, y, z, n, m, cnt = 0;cin >> x >> y >> z >> n >> m;for (int i = 0; i <= n / x && i <= m; i++) {for (int j = 0; j <= (n - i * x) / y && j <= m - i; j++) {int k = m - i - j;if (k >= 0 && k % z == 0) { //可以if(k%z||k<0) continue;if (i * x + j * y + k / z == n) { //这两个if条件可以合并在一起cnt++;}}}}cout << cnt;return 0;
}