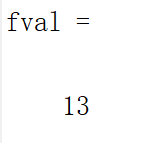当前位置：首页 > web >正文

数学建模——01规划/整数规划

web 2025/7/31 9:24:29

1.概念

数学规划问题有些数据必须是整数，但是理论最优解可能是小数，比如人数，这一类数据只能是整数。如果

要求解的数据全是整数	整数规划
要求解的数据有一部分限制是整数	混合整数规划
解只能取0或者1的规划	01规划

2.函数

整数线性规划是可以用matlab求解的

	线性规划	非线性规划	整数规划
模型标准型	$min \; \; \; f(x)$ $s.t.\left\{\begin{matrix} Ax\leq b,Aeq\cdot x=beq \\ lb\leq x\leq ub \end{matrix}\right.$	$min \; \; \; f(x)$ $s.t.\left\{\begin{matrix} Ax\leq b,Aeq\cdot x=beq \\ c(x)\leq 0,Ceq(x)=0 \\ lb\leq x\leq ub \end{matrix}\right.$
函数名	linprog	fmincon	intlinprog
函数用法	`[x, fval] = linprog(f, A, b, Aeq, beq, lb,ub);`	`[x, fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,option);`	`[x, fval] = intlinprog(f,intcon, A, b, Aeq, beq, lb,ub,x0);`

参数含义：

linprog		fmincon		intlinprog
f	目标函数系数向量（列向量）	fun	把目标函数定义成一个单独的函数文件（min）	f	目标函数系数向量（列向量）
A	不等式约束矩阵（左侧系数）	x0	决策变量的初始值	intcon	是指决策变量x中应该取整数值的分量，比如决策变量有三个 $x_1,x_2,x_3$ 若1，3是整数，那么intcon = [1,3]
b	不等式约束右侧常数向量	A,b	线性约束不等式变量系数矩阵和常数项矩阵（左侧系数和右侧向量，支持 $\leq or<$ ）	A,b	线性约束不等式变量系数矩阵和常数项矩阵（左侧系数和右侧向量，支持 $\leq or<$ ）
Aeq	等式约束矩阵（`Aeq`），空表示无等式约束	Aeq,beq	线性约束等式变量系数矩阵和常数项矩阵（左侧系数和右侧向量）	Aeq,beq	线性约束等式变量系数矩阵和常数项矩阵（左侧系数和右侧向量）
beq	等式约束右侧常数向量（`beq`），空表示无等式约束	lb,ub	决策变量的最小与最大取值（变量上下界）	lb,ub	决策变量的最小与最大取值（变量上下界）
lb	变量下界（lower bound）	nonlcon	非线性约束（包括不等式与等式）
ub	变量上界（upper bound）	option	求解非线性规划使用的方法

备注：01变量就是整数规划的变式，只需要把lb，ub改成限制在0和1之间的整数就行

例题：

1.01背包问题

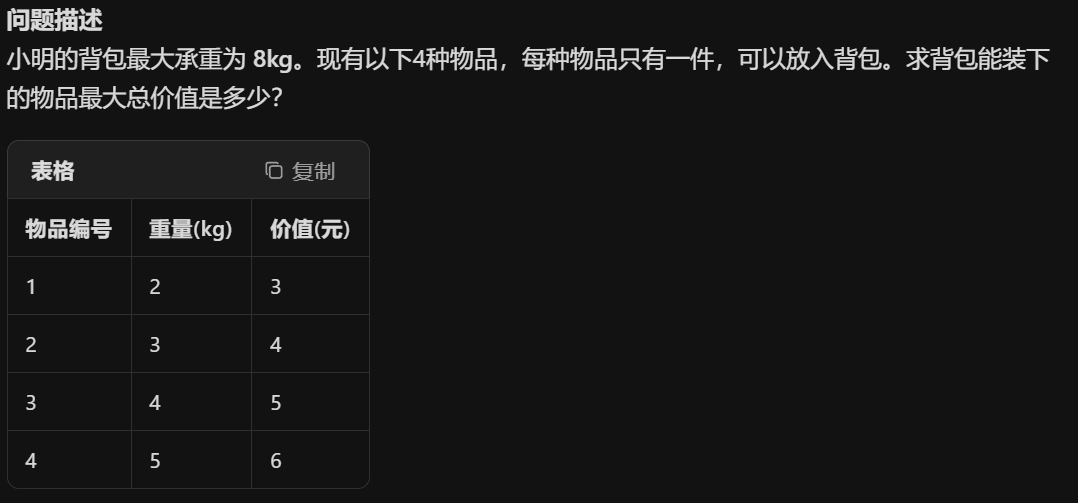
1.记录xi=1表示第i件物品装入背包，0表示没装

2.用wi表示第i件物品重量，pi表示第i件物品的价值,得到:

$max \; \; \sum_{i=1}^{10} p_ix_i$

$s.t.\left\{\begin{matrix} \sum_{i=1}^{4}w_ix_i\leq 8 \\ x_i\in \left \{ 0,1 \right \} \end{matrix}\right.$

但是前面说过这类函数只能求最小值，因此要转化

$min \; \; -\sum_{i=1}^{10} p_ix_i$

$s.t.\left\{\begin{matrix} \sum_{i=1}^{4}w_ix_i\leq 8 \\ x_i\in \left \{ 0,1 \right \} \end{matrix}\right.$

%01背包和整数规划
c=-[3 4 5 6];
intcon=[1:4];
A=[2 3 4 5];
b=8;
Aeq=[];beq=[];
lb=zeros(4,1);
ub=ones(4,1);
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub);
fval=-fval;
x
fval

2.指派类问题

员工：i=1，2，3，4

四项任务：j=1，2，3，4

$x_{ij}=1$ 表示员工i选择第j种任务，0表示不选择第j种任务

$t_{ij}$ 表示员工i完成第j种任务用时

$min\; \; \sum_{j=1}^{4}\sum_{i=1}^{4}t_{ij}x_{ij}$

$s.t.\left\{\begin{matrix} \sum_{j=1}^{4}x_{ij}=1,i=1,2,3,4 \\ \sum_{i=1}^{4}x_{ij}=1,j=1,2,3,4 \\ x_{ij}\in \left \{ 0,1 \right \} \end{matrix}\right.$

第一行表示每个人都能且仅能选择一项任务

第二行表示每种任务都交给一个人完成

%指派问题
%转单下标
c=[9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4];
intcon=[1:16];
A=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
b=ones(4,1);
Aeq=repmat(eye(4),1,4);
beq=ones(4,1);
lb=zeros(16,1);
ub=ones(16,1);
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub);
newx=reshape(x,4,4)
fval

虽然跑出来结果是正确的，但是这里有问题，因为A按理来说应该是不等式，所以正确的应该是

%转单下标
c=[9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4];
intcon=[1:16];
A=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
b=ones(4,1);
Aeq=repmat(eye(4),1,4);
beq=ones(4,1);realAeq=[A;Aeq];
realbeq=[b;beq];lb=zeros(16,1);
ub=ones(16,1);
[x,fval]=intlinprog(c,intcon,[],[],realAeq,realbeq,lb,ub);
newx=reshape(x,4,4)
fval

变式：假如有人可以不参加

员工：i=1，2，3，4，5

四项任务：j=1，2，3，4

$x_{ij}=1$ 表示员工i选择第j种任务，0表示不选择第j种任务

$t_{ij}$ 表示员工i完成第j种任务用时

$min\; \; \sum_{j=1}^{5}\sum_{i=1}^{4}t_{ij}x_{ij}$

$s.t.\left\{\begin{matrix} \sum_{j=1}^{5}x_{ij}\leq 1,i=1,2,3,4,5 \\ \sum_{i=1}^{4}x_{ij}=1,j=1,2,3,4 \\ x_{ij}\in \left \{ 0,1 \right \} \end{matrix}\right.$

第一行表示每个人都能且仅能选择一项任务或者不完成任务

第二行表示每种任务都交给一个人完成

% 指派问题
% 转单下标
c=[9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 6 5 8 5];
intcon=[1:20];
A=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
b=ones(5,1);
Aeq=repmat(eye(4),1,5);
beq=ones(4,1);
lb=zeros(20,1);
ub=ones(20,1);
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub);
count=1;newx=zeros(5,4);
for i=1:5for j=1:4newx(i,j)=x(count);count=count+1;end
end
newx
fval