基于MATLAB的泊松分布，正态分布与伽玛分布（附完整代码与例题）_matlab泊松分布(1)

给大家的福利

零基础入门

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

同时每个成长路线对应的板块都有配套的视频提供：

因篇幅有限，仅展示部分资料

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以点击这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

y2=[y2,poisscdf(x,lam1(i))];

end
plot(x,y1), figure; %figure命令可让其画两个图
plot(x,y2)

注意题目要求是画曲线，所以需要将这些点连起来。泊松概率密度函数图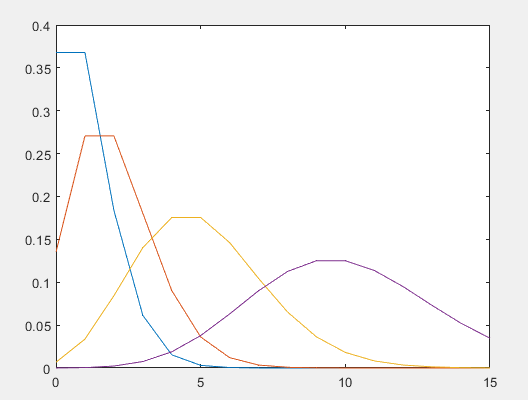：![](https://img-blog.csdnimg.cn/direct/4081047a998541efac765b64c1cef9f3.png)泊松分布的概率分布函数图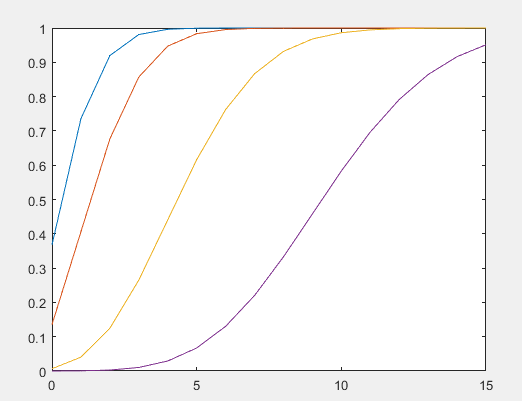：![](https://img-blog.csdnimg.cn/direct/5ac48fe52414413bb2342357572aafe5.png)## 二. 正态分布### 2.1 理论部分正态分布的概率密度函数如下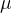：![p(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}](https://latex.csdn.net/eq?p%28x%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%5Csigma%7D%7De%5E%7B-%5Cfrac%7B%28x-%5Cmu%29%5E2%7D%7B2%5Csigma%5E2%7D%7D)其中![\mu](https://latex.csdn.net/eq?%5Cmu)代表均值，![\sigma^2](https://latex.csdn.net/eq?%5Csigma%5E2)代表方差。### 2.2 MATLAB函数模型正态分布的概率密度函数，在MATLAB中可以直接调用：

y=normpdf(x,mu,sigma);

%给定x,mu,sigma的值，就可以直接求该点的概率密度值
%注意函数调用格式中的sigma使用的是标准差

分布函数（累积概率函数），在MATLAB中可以直接调用：

F=normcdf(x,mu,sigma);

如果给定分布函数值，反过来求x，则需要调用逆概率分布函数：

x=norminv(F,mu,sigma);

### 2.3 例题分别绘制出![(\mu,\sigma^2)](https://latex.csdn.net/eq?%28%5Cmu%2C%5Csigma%5E2%29)为(-1,1),(0,0.1),(0,1),(0,10),(1,1)时，正态分布的概率密度函数与分布函数曲线。MATLAB代码：

x=[-5:.02:5]';
y1=[];
y2=[];
mu1=[-1,0,0,0,1];
sig1=[1,0.1,1,10,1]; sig1=sqrt(sig1); %注意函数调用的是标准差
for i=1:length(mu1) %length(mu1)=5
y1=[y1,normpdf(x,mu1(i),sig1(i))];
y2=[y2,normcdf(x,mu1(i),sig1(i))];
end
plot(x,y1), figure;
plot(x,y2)

正态分布的概率密度函数图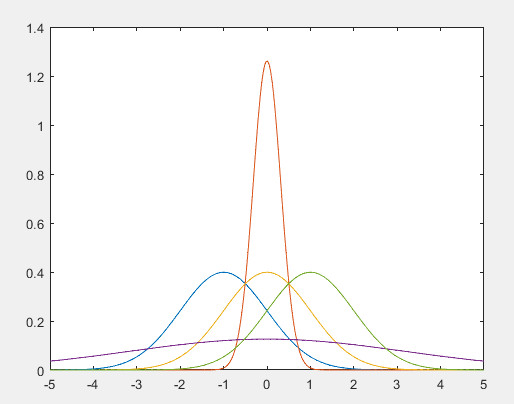：![](https://img-blog.csdnimg.cn/direct/d816b7f58803494d9f18958bce77d568.png)根据对称轴的值，也就是均值的大小可以对应曲线代表的正态分布。方差越大，曲线越胖。分布函数曲线图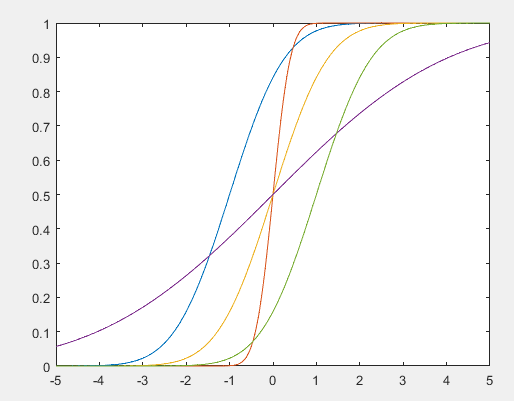：![](https://img-blog.csdnimg.cn/direct/bcd162eea7a24b60a1bdac825b0107b7.png)函数严格单调递增。## 三. 伽玛分布### 3.1 理论部分观察相邻两个事件之间时间间隔的分布情况，或者隔k个事件的时间间隔的分布情况。根据概率论，事件之间的时间间隔应符合伽玛分布，由于时间间隔可以是任意数值，因此伽玛分布是一种连续概率分布。又因为时间间隔不可能为负数，所以伽玛分布的x需要非负。伽玛分布有的时候也会写做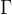![\Gamma](https://latex.csdn.net/eq?%5CGamma)分布，其概率密度函数为：![P_\Gamma(x)=\begin{cases} \frac{\lambda^ax^{a-1}}{\Gamma(a)}e^{-\lambda x},\quad &x\geq 0 \\ 0,\quad &x<0 \end{cases}](https://latex.csdn.net/eq?P_%5CGamma%28x%29%3D%5Cbegin%7Bcases%7D%20%5Cfrac%7B%5Clambda%5Eax%5E%7Ba-1%7D%7D%7B%5CGamma%28a%29%7De%5E%7B-%5Clambda%20x%7D%2C%5Cquad%20%26x%5Cgeq%200%20%5C%5C%200%2C%5Cquad%20%26x%3C0%20%5Cend%7Bcases%7D)伽玛分布需要提前确定两个参数：a与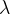![\lambda](https://latex.csdn.net/eq?%5Clambda).上个式子中：![\Gamma(a)=\int_0^\infty x^{a-1}e^{-x}dx](https://latex.csdn.net/eq?%5CGamma%28a%29%3D%5Cint_0%5E%5Cinfty%20x%5E%7Ba-1%7De%5E%7B-x%7Ddx)在MATLAB可以调用积分函数来计算该值，也可以直接调用gamma()函数来计算，两种途径都可以。该积分属于指数积分类型，有三个常用的结论：![\Gamma(a)=a\Gamma(a-1)](https://latex.csdn.net/eq?%5CGamma%28a%29%3Da%5CGamma%28a-1%29)![\Gamma(1)=1](https://latex.csdn.net/eq?%5CGamma%281%29%3D1)![\Gamma(\frac{1}{2})=\pi](https://latex.csdn.net/eq?%5CGamma%28%5Cfrac%7B1%7D%7B2%7D%29%3D%5Cpi)### 3.2 MATLAB函数模型与泊松分布和正态分布类似，此处也有对应的三个函数，就不过多啰嗦了：

%概率密度函数
y=gampdf(x,a,lambda)

%概率分布函数
F=gamcdf(x,a,lambda)

%逆概率分布函数
x=gaminv(F,a,lambda)

### 3.3 例题绘制![(a,\lambda)](https://latex.csdn.net/eq?%28a%2C%5Clambda%29)为(1,1),(1,0.5),(2,1),(1,2),(3,1)时伽玛分布的概率密度函数与分布函数曲线。MATLAB代码：

x=[-0.5:.02:5]'; %图像x轴取值范围
y1=[]; y2=[];
a1=[1,1,2,1,3];
lam1=[1,0.5,1,2,1];
for i=1:length(a1)
y1=[y1,gampdf(x,a1(i),lam1(i))];
y2=[y2,gamcdf(x,a1(i),lam1(i))];
end
plot(x,y1), figure; plot(x,y2)

概率密度函数曲线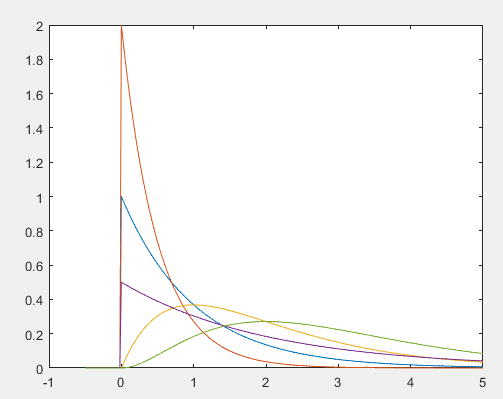：![](https://img-blog.csdnimg.cn/direct/19c71a6fa5cc4459a12495d38d2c8a40.png)伽马函数的图像趋势一般是先上升后下降。## 学习路线：这个方向初期比较容易入门一些，掌握一些基本技术，拿起各种现成的工具就可以开黑了。不过，要想从脚本小子变成黑客大神，这个方向越往后，需要学习和掌握的东西就会越来越多以下是网络渗透需要学习的内容：  ![在这里插入图片描述](https://img-blog.csdnimg.cn/7a04c5d629f1415a9e35662316578e07.png#pic_center)**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。****[需要这份系统化资料的朋友，可以点击这里获取](https://bbs.csdn.net/forums/4f45ff00ff254613a03fab5e56a57acb)****一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**