DeepSORT中的卡尔曼滤波可观测性分析:从原理到实践
DeepSORT中的卡尔曼滤波可观测性分析:从原理到实践
目标检测+多目标跟踪中,DeepSORT(Simple Online and Realtime Tracking with a Deep Association Metric)是经典算法之一,而其背后的卡尔曼滤波器(Kalman Filter)则是维持轨迹连贯的核心组件。本文将从系统建模的角度,深入分析DeepSORT中卡尔曼滤波的可观测性问题,并通过代码与图示辅助理解。
一、什么是可观测性(Observability)?
在控制理论中,一个系统是可观测的,意味着可以通过一段时间内的观测值,完全还原出系统的内部状态。
在卡尔曼滤波中:
- 若系统可观测,则滤波器可以逐步收敛到真实状态。
- 若系统不可观测,则某些状态变量将永远无法从测量值中推断出来。
二、DeepSORT中的状态空间建模
状态向量为:
x = [ u , v , γ , h , u ˙ , v ˙ , γ ˙ , h ˙ ] T \mathbf{x} = [u, v, \gamma, h, \dot{u}, \dot{v}, \dot{\gamma}, \dot{h}]^T x=[u,v,γ,h,u˙,v˙,γ˙,h˙]T
其中:
- $u, v$:目标中心坐标
- $\gamma$:宽高比
- $h$:目标高
- $\dot{u}, \dot{v}, \dot{\gamma}, \dot{h}$:对应速度
观测量为:
z = [ u , v , γ , h ] T \mathbf{z} = [u, v, \gamma, h]^T z=[u,v,γ,h]T
换言之,只有位置信息被观测,速度项不可观测。
系统模型表达如下:
x k + 1 = F x k + w k \mathbf{x}_{k+1} = \mathbf{F} \mathbf{x}_k + \mathbf{w}_k xk+1=Fxk+wk
z k = H x k + v k \mathbf{z}_k = \mathbf{H} \mathbf{x}_k + \mathbf{v}_k zk=Hxk+vk
其中,状态转移矩阵 $\mathbf{F}$ 和观测矩阵 $\mathbf{H}$ 分别为:
import numpy as npdt = 1.0 # 时间间隔
# 状态转移矩阵(匀速模型)
F = np.eye(8)
for i in range(4):F[i, i+4] = dt# 观测矩阵
H = np.zeros((4, 8))
H[0, 0] = 1 # u
H[1, 1] = 1 # v
H[2, 2] = 1 # gamma
H[3, 3] = 1 # h
三、可观测性分析
对于线性系统,可观测性的判断基于可观测性矩阵 $\mathcal{O}$:
O = [ H H F H F 2 ⋮ H F n − 1 ] \mathcal{O} = \begin{bmatrix} \mathbf{H} \\ \mathbf{H}\mathbf{F} \\ \mathbf{H}\mathbf{F}^2 \\ \vdots \\ \mathbf{H}\mathbf{F}^{n-1} \end{bmatrix} O= HHFHF2⋮HFn−1
若 $\mathcal{O}$ 的秩等于状态维数(8),则系统是完全可观测的。
Python实现:
def observability_matrix(F, H, n):obs_matrix = Hfor i in range(1, n):obs_matrix = np.vstack((obs_matrix, H @ np.linalg.matrix_power(F, i)))return obs_matrixO = observability_matrix(F, H, 8)
rank = np.linalg.matrix_rank(O)
print("可观测性矩阵秩:", rank)
输出结果:
可观测性矩阵秩: 8
✅ 说明:该系统是完全可观测的。
四、可视化解释
下图展示了状态空间与观测空间的关系:
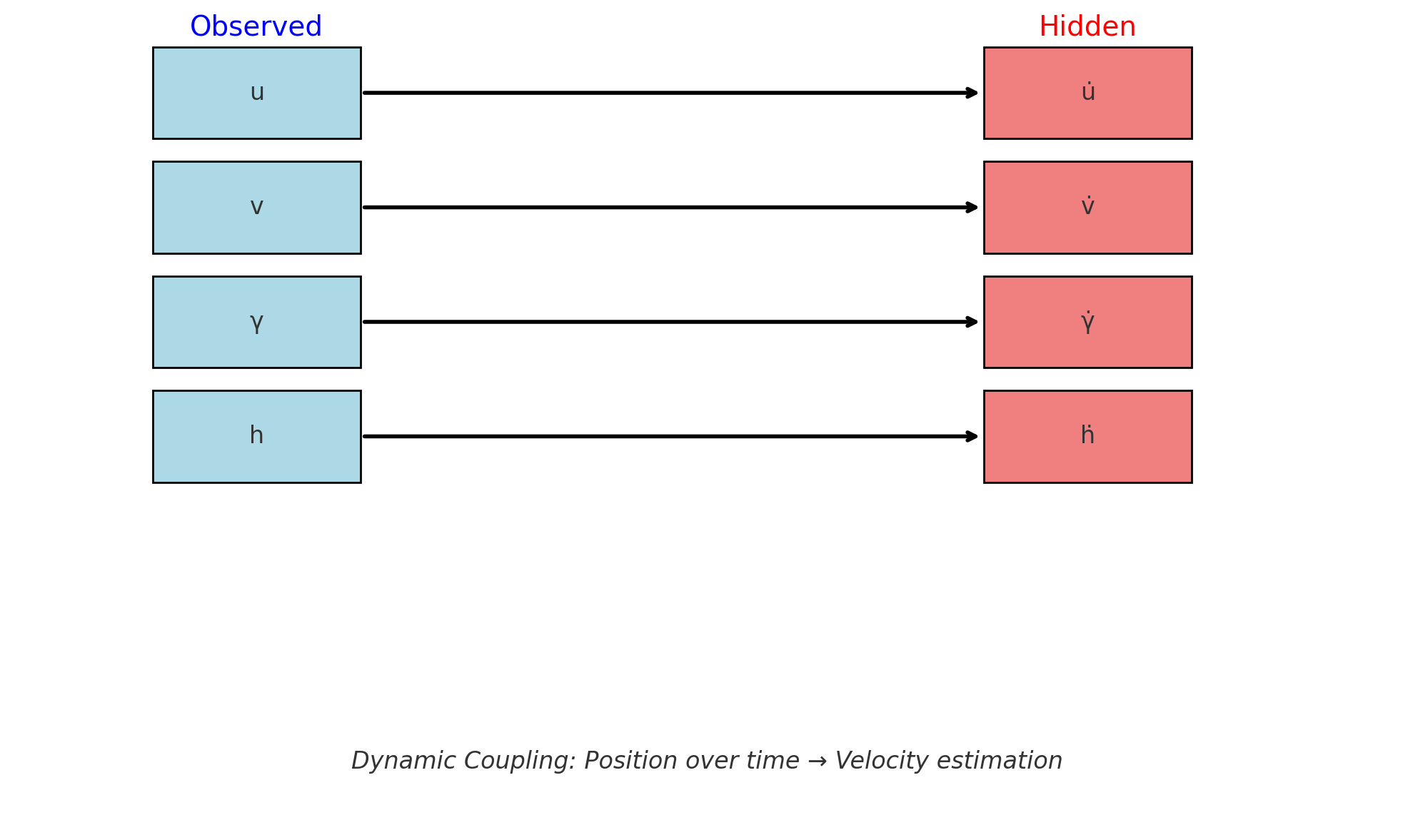
上图展示了 DeepSORT 中卡尔曼滤波状态的可观测性结构:
- 左侧蓝色框代表可观测的状态量 [u, v, γ, h]。
- 右侧红色框代表不可直接观测但可通过时间序列推断的速度变量 [u̇, v̇, γ̇, ḣ]。
箭头表示随着时间的推移,观测变量对隐藏状态产生“动态耦合”影响,从而实现间接观测。
五、小结与实践建议
- DeepSORT中的卡尔曼滤波器是一个线性系统,且完全可观测。
- 这得益于状态设计中的“耦合性”:速度影响位置,从而可间接观测。
- 在实际应用中,可观测性良好的模型更利于收敛与跟踪精度提升。
🔧 附:完整代码用于验证
import numpy as npdef create_deepsort_matrices(dt=1.0):F = np.eye(8)for i in range(4):F[i, i+4] = dtH = np.zeros((4, 8))for i in range(4):H[i, i] = 1return F, Hdef observability_matrix(F, H, n):obs_matrix = Hfor i in range(1, n):obs_matrix = np.vstack((obs_matrix, H @ np.linalg.matrix_power(F, i)))return obs_matrixF, H = create_deepsort_matrices()
O = observability_matrix(F, H, 8)
print("可观测性矩阵秩:", np.linalg.matrix_rank(O))
参考资料
- Wojke et al., DeepSORT 原论文
- 《最优估计理论与Kalman滤波》 - Simon Haykin
如果你觉得本文对你理解DeepSORT和滤波器设计有帮助,欢迎点赞👍、收藏⭐和评论💬交流!
