【数据结构——哈夫曼树】

引入

（懒得再整，将就看吧~）

详述

像D+B=3，D和B都指向3这句话：指向标为3的这个节点，3是这个节点的权，实际上这个节点可以说是新节点，当然是以抽象模型来看，因为实际是已经申请固定大小空间的数组，“新节点”的相关内容就依次填在数组对应的各类空间中。
比如以下表格中按每个字母的权进行整理成哈夫曼树的形式：

先找最小权，再找次小权：3（G）、5（A），让它们指向一个权为两者权之和的新节点（8）；再重复找最小权、次小权，重复操作。

当出现即将要找的节点的权即大于老节点又小于老节点时（比如找完了3、5、7、8之后该找11了，这时候11既大于3+5生成的的节点，又小于7+8生成的节点），这时候就要将这些组队生成的节点当作自用节点（就是本身就有的，可以支配的），继续组队，组队顺序依旧先左后右，优先插左子树上。那就和8组队生成一个新节点，就这样类比操作。

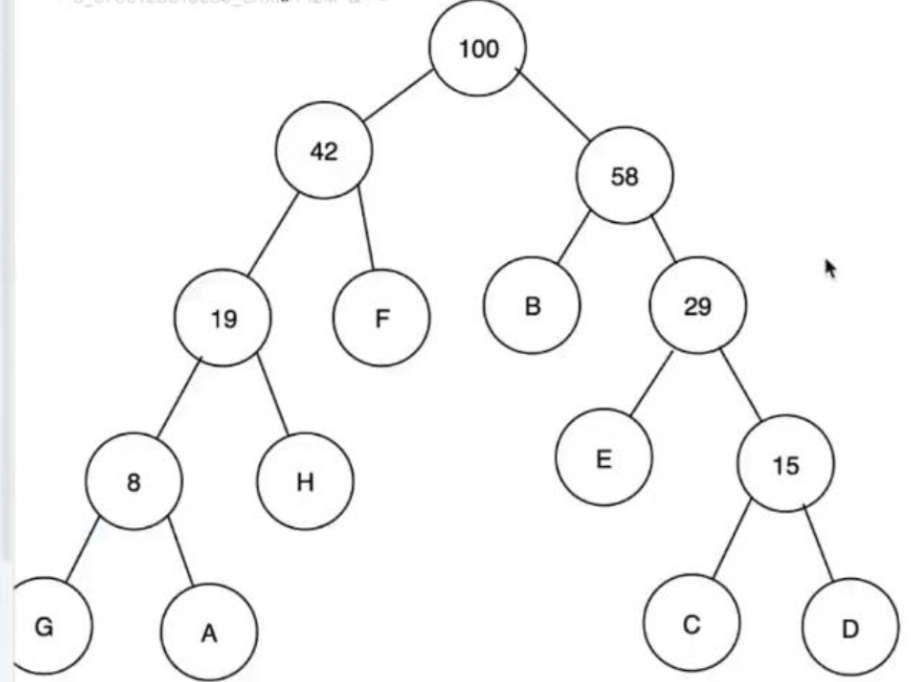
思路

像之前说过，它实际是数组空间不同类的数据。那现在如何将这种思想实现出来？首先上图所说的新节点就是继原数据编号之后的空间，依次从第一个（存原始数据之后的空间的第一个空间编号）到最后一个进行填充。

比如现在有八个数据（A~H），空间编号到8，那新节点就从编号9开始存关系数据（自身的权，自己的父节点、左孩子、右孩子的编号）。

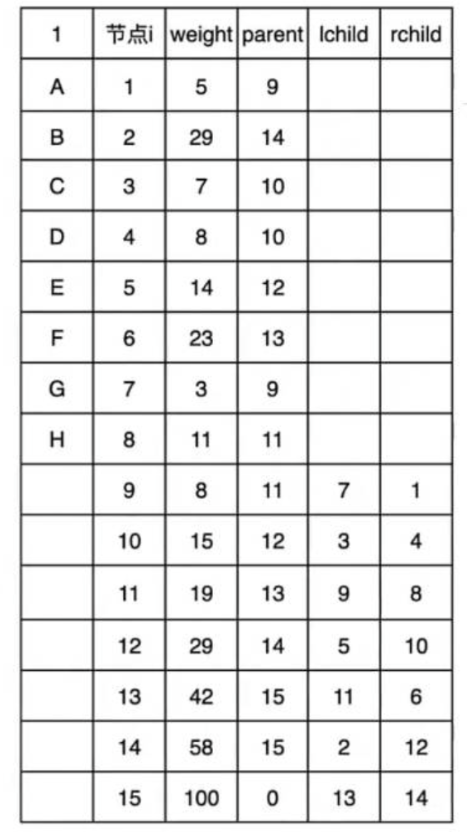
到这里为了方便查看就将树的图上面段话复制下来了:
先找最小权，再找次小权：3（G）、5（A），让它们指向一个权为两者权之和的新节点（8）:这里权为3和5的这两个节点的父节点的编号都为9。编号9的父节点依旧是初始值0，但左孩子的编号是3，右孩子的编号是5，权为8（3+5）。
就这样再重复找最小权、次小权，再修改数组中各项对应值。

当出现即将要找的节点的权即大于老节点又小于老节点时（比如找完了3、5、7、8之后该找11（编号8）了，这时候11既大于3+5生成的的节点（编号9），又小于7+8生成的节点：编号10），这时候就要将这些组队生成的节点当作自用节点（就是本身就有的，可以支配的），继续组队，组队顺序依旧先左后右，优先插左子树上。那就和8（编号9，权为8）组队生成一个新节点（编号10已经用了，继续往后用：编号11），那现在编号9和编号8的父节点的编号都为编号11，编号11的左孩子是9，右孩子是8，权为8+11=19，就这样类比操作。

头文件

#pragma once
typedef struct {int weight;int parent;int lChild;int rChild;
}HuffmanNode,*HuffmanTree;HuffmanTree createHuffmanTree(const int* w, int n);typedef char* HuffmanCode;
//依据Huffman树产生n个Huffman编码
HuffmanCode* createHuffmanCode(HuffmanTree tree, int n);void releaseHuffmanCode(HuffmanCode* codes, int n);

功能实现

预处理命令

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include"huffmanTree.h"
#include <corecrt_memory.h>
#include<string.h>

选出两个权值最小的节点

static void selectNode(HuffmanTree tree, int n, int* s1, int* s2) {int mini = 0;//先找父节点为0的编号（编号从1开始，0空着）for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0) {mini = i;break;}}//再找父节点为0的编号中所属权值最小的编号for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0) {if (tree[i].weight < tree[mini].weight) {mini = i;}}}*s1 = mini;  //找到并标记权值最小的点//开始找权值次小点（除mini之外的权值最小点）for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0 && i != *s1) {mini = i;break;}}for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0 && i != *s1) {if (tree[i].weight < tree[mini].weight) {mini = i;}}}*s2 = mini;
}

创建哈夫曼树

HuffmanTree createHuffmanTree(const int* w, int n) {HuffmanTree tree;//以树的结构看：每两个最小节点合并就新增一个节点（两最小节点的父节点）//该节点又会与另外的一个节点合并生成新节点//每个节点最多结合1次,除了树根,其他都合并出了新节点// 共结合n-1次，新增n-1个节点,原本有n个节点，共n+(n-1)=(2*n-1)个节点int m = 2 * n - 1;//申请2n个单元，从1号开始存，0号不存数据tree = (HuffmanNode*)malloc(sizeof(HuffmanNode) * (m + 1));if (tree == NULL) {return NULL;}//初始化1~2n-1这些节点for (int i = 1; i <= m; ++i) {tree[i].lChild = tree[i].rChild = tree[i].parent = 0;tree[i].weight = 0;}//设置初始化权值for (int i = 1; i <= n; ++i) {tree[i].weight = w[i - 1];}
//像之前所说:两节点结合生成的新节点的数据存储在编号n后面的存储单元
//所以从编号n+1开始填充，一直到编号m的空间int s1, s2;for (int i = n + 1; i <= m; ++i) {selectNode(tree, i - 1, &s1, &s2);
//找1~i-1范围内两个最小点并结合到n+1位置上tree[s1].parent = tree[s2].parent = i;tree[i].lChild = s1;tree[i].rChild = s2;tree[i].weight = tree[s1].weight + tree[s2].weight;}return tree;
}

创建编码表

HuffmanCode* createHuffmanCode(HuffmanTree tree, int n) {//生成n个字符的编码表HuffmanCode* codes = (HuffmanCode*)malloc(sizeof(HuffmanCode)*n);if (codes == NULL) {return NULL;}memset(codes, 0, sizeof(HuffmanCode) * n);// 每求一个字符时，倒序构建(一般从根节点开始往下找为正序，现在从叶子节点开始)//共n个节点，树的高度最高是n，编码个数最多为n，那temp最多存n个编码char* temp = (char*)malloc(sizeof(char) * n);int start;				// temp空间的起始位置，从后往前int p;					// 存放当前节点的父节点信息,再逐个往上找根节点int pos;				// 当前编码的位置// 逐个字符求Huffman编码(只需要为叶子节点生成编码，所以是1~n,共n个节点)for (int i = 1; i <= n; ++i) {start = n - 1; //temp空间编号从0开始的，所以要再减1temp[start] = '\0'; //先存占位符，后面存对应编码pos = i;p = tree[i].parent;while (p) {  //当前节点的父节点的编号不为0时执行（继续找）--start; //先一步到父节点（反应节点之间关系，方便判断左右）temp[start] = (tree[p].lChild == pos) ? '0' : '1';pos = p;p = tree[p].parent;}// 第i个字符编码分配的空间(n-start是有效编码长度:start是递减到根节点为止)//共n个叶子节点，编码部分就是start递减的部分：n-startcodes[i - 1] =(char*) malloc(sizeof(HuffmanCode) * (n - start));//拷贝成正序，i-1是从0开始，start从n-1开始strcpy(codes[i - 1], &temp[start]);}free(temp);return codes;
}

释放编码表

void releaseHuffmanCode(HuffmanCode* codes, int n) {if (codes) {for (int i = 0; i < n; ++i) {if (codes[i]) {free(codes[i]);}}}
}

overover~