当前位置：首页 > ops >正文

力扣hot100:螺旋矩阵（边界压缩，方向模拟）（54）

ops 2025/9/6 9:16:35

在解决螺旋矩阵问题时，我们需要按照顺时针螺旋顺序遍历矩阵，并返回所有元素。本文将分享两种高效的解决方案：边界收缩法和方向模拟法。

题目描述

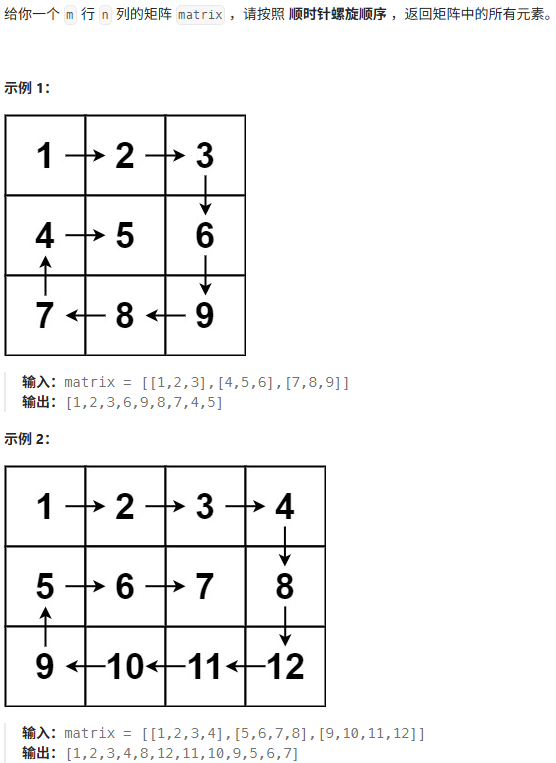
边界收缩法

边界收缩法通过定义四个边界（上、下、左、右）来模拟螺旋遍历的过程。每完成一个方向的遍历，就收缩对应的边界，直到所有元素被访问完毕。

算法思路

初始化边界：top = 0, bottom = m-1（行数-1）, left = 0, right = n-1（列数-1）。
按层遍历：
- 向右：遍历上边界（top行），从 left 到 right。
- 向下：遍历右边界（right列），从 top+1 到 bottom。
- 向左：遍历下边界（bottom行），从 right-1 到 left+1（需确保存在内层）。
- 向上：遍历左边界（left列），从 bottom 到 top+1（需确保存在内层）。
收缩边界：完成一圈后，将 top++, bottom--, left++, right--。
终止条件：当边界交错时停止（top > bottom 或 left > right）。

代码实现

class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result=new ArrayList<Integer>();int x= matrix.length;int y=matrix[0].length;int left=0;int right=y-1;int top=0;int bottom=x-1;while(left<=right&&top<=bottom){for(int i=left;i<=right;i++){result.add(matrix[top][i]);}for(int i=top+1;i<=bottom;i++){result.add(matrix[i][right]);}if(left<right&&top<bottom) {for (int i = right - 1; i > left; i--) {result.add(matrix[bottom][i]);}for (int i = bottom; i > top; i--) {result.add(matrix[i][left]);}}left++;right--;top++;bottom--;}return result;}
}

复杂度分析

时间复杂度：O(m*n)，每个元素被访问一次。
空间复杂度：O(1)，仅使用常量额外空间（结果列表不计入）。

方向模拟法（其他解决方案）

方向模拟法通过定义方向数组和记录访问状态来模拟螺旋路径，适合对边界条件处理不熟悉的情况。

算法思路

初始化：
- 方向数组 dirs 表示右、下、左、上四个方向。
- 访问矩阵 visited 记录元素是否被访问。
- 从 (0,0) 开始，初始方向为右。
遍历矩阵：
- 将当前元素加入结果列表，并标记为已访问。
- 计算下一个位置，若越界或已访问，则顺时针转向。
- 更新位置并继续遍历，直到所有元素被访问。

代码实现

class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0) return result;int m = matrix.length, n = matrix[0].length;boolean[][] visited = new boolean[m][n];int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 右、下、左、上int r = 0, c = 0, d = 0;int total = m * n;for (int i = 0; i < total; i++) {result.add(matrix[r][c]);visited[r][c] = true;// 计算下一个位置int nr = r + dirs[d][0];int nc = c + dirs[d][1];// 若越界或已访问，则转向if (nr < 0 || nr >= m || nc < 0 || nc >= n || visited[nr][nc]) {d = (d + 1) % 4; // 顺时针转向nr = r + dirs[d][0];nc = c + dirs[d][1];}r = nr;c = nc;}return result;}
}