当前位置：首页 > ops >正文

中心扩展算法

ops 2025/9/2 14:42:43

大家好，今天是2025年9月1日，我要来给大家分享的是一种针对于回文字符串的算法：中心扩展算法。希望对大家能够有所帮助。

一：相关概念

1.【回文字符串】

正着和反着读都一样的字符串就是回文字符串；或者中心画线左右对称的字符串就是回文字符串。

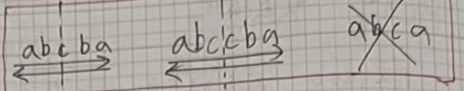
注意：单独一个字符我们也认为是回文字符串

如果回文串的长度为奇数，则称该回文串为奇回文串。如果回文串的长度为偶数，则称该回文串为偶回文串。

如何判断一个字符串是否回文？？？------1.逆序，2.双指针。

2.【回文子串】

字符串中的某个子串如果是回文，那么就是回文子串。

其中，所有回文子串中长度最长的被称为最长回文子串。

3.【性质】

如果一个字符串是回文串，那么依次删掉首尾两个字符后，依旧是回文。

证明的话就用对称性就行了。画几个图看一看就OK了~~

应用：使用这个性质，当我们知道以某个点为中心的最长回文子串之后，就能够找到以这个点为中心的所有回文串。（不断向中心点收缩）

4.【回文中心和回文半径】

回文中心，用 c 表示，顾名思义，就是回文串中最中心的位置。

如果是奇回文串，回文中心在（n + 1）/ 2 的位置，如 “abcba”；

如果是偶回文串，回文中心在【n / 2，n / 2 + 1】之间，如 “aabbaa”；

回文半径，用 d 表示，表示回文中心到回文串首尾端点的距离。中心点也算

例如：回文串 “abcba” 的回文半径为 3；回文串 “aabbaa” 的回文半径也是 3。

有了回文中心和回文半径，我们就可以在字符串中表示出一个回文子串。

例如：在字符串 “caababaae” 中，有一个 c = 5，d = 4 的回文子串，有一个c = 5，d = 2 的回文子串等等。

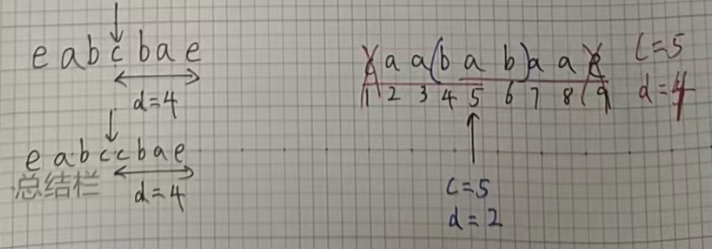
二：中心扩展算法

1.【问题】

对于回文串，我们经常遇到下面的问题：

问题一：在一个字符串中，找到所有的回文子串。
问题二：在一个字符串中，找出最长的回文子串。

上述两个问题本质上可以看作一个问题，因为如果我们能够找到所有的回文子串，肯定也能找到最长的回文子串。

2.【中心扩展算法】

中心扩展算法可以在 O（n ^ 2）的时间内解决上面的问题，算法原理非常简单，枚举所有的中心点 c，从中间向两边扩展，知道首尾字符不同为止。

具体步骤：

从前往后遍历字符串，以 s[i] 或 s[i] 与 s[i + 1] 的中间作为回文串的中心位置；
从中间位置开始，枚举回文半径长度，逐渐向两边扩展，找出以该点为中心的最长回文子串。

最长的回文子串既可能是奇回文串，也可能是偶回文串，因此我们不仅要寻找奇回文也要寻找偶回文。

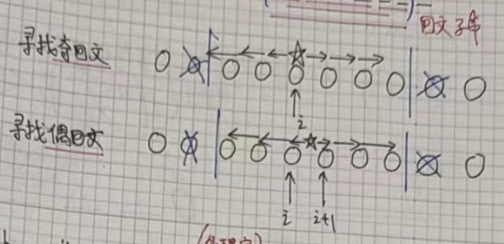
我们发现，奇偶回文会让我们在找回文子串的时候分类讨论。问了避免这种情况，我们采取下面的方法，把所有的回文子串都变成奇回文串。（很巧妙的一个方法）

因为奇回文串通常比偶回文串好处理：它只有一个中心，而且可以从中心向两边一步一步扩展得到。

3.【预处理字符串】

我们在字符串相邻的字符之间以及整个字符串的两端任意加入一个字符（一般使用 ‘#’）。

预处理完毕之后，本来的奇回文串还是奇回文串，本来的偶回文串会变成奇回文串。

因为预处理操作之后，字符串的长度会比原来字符串长度的两倍多一，（2n + 1）的话一定会是奇数。

这样预处理的话，字符串中就不会存在偶回文字串了。

注意：这里的话不用像我们之前学过的 KMP 算法一样，加入一个不会出现的字符，我们可以加入任意字符。

因为判断回文的时候，原有的字符会跟原有的字符比对，新加入的字符会和新加入的字符比对。

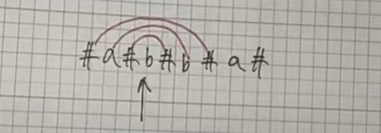
规律：处理之后的最长回文半径 - 1 = 处理之前的回文串的长度（多模拟几个案例就行了）。

4.【代码实现】

string s, t; // s 是预处理之后的字符串 
int m, n;// 以求解最长回文子串为例
int fun()
{// 预处理字符串cin >> t; m = t.size();s += ' ';for(auto ch : t){s += '#';s += ch;} s += "##";n = s.size() - 2;int ret = 1;// 中心扩展算法 for(int i = 1; i <= n; i++){int d = 1; // 枚举向右向左的距离 while(s[i - d] == s[i + d]) d++;ret = max(ret, d - 1);}return ret;
}

解释：这里为什么要在字符串的末端多加入一个 ‘#’ ？？？