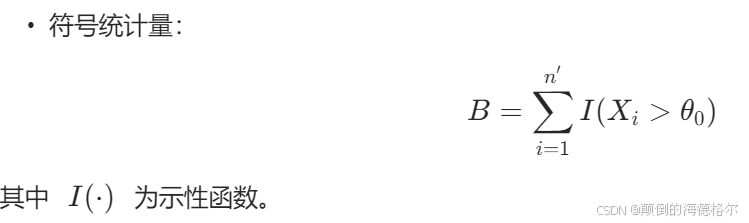参数检验vs非参数检验

之所以出这篇博客，除了记录备份自己以往的草稿之外，还是因为这几年经过统计学习的总结，

发现很多人（包括一些所谓CNS子刊）的统计问题，

问题不在于不会使用统计方法，而在于使用不精。

常见问题有：
1️⃣ 忽略统计方法的使用前提条件（数学敏感性不足）

2️⃣ 无法区分几种类似统计方法的差别（统计学不成体系）

3️⃣ 根据自己想要得到的结果，却不根据问题选择统计方法（纯属统计学文盲，严格来说可以定性为学术造假）

在假设检验中，统计检验用于检查零假设是否被拒绝。这些统计检验假设了一个零假设，即各组之间没有关系或没有差异。

总的来说，假设检验是统计推论中用于检验现有数据是否足以支持特定假设的方法。

一旦能估计未知参数，就会希望根据结果对未知的真正参数值做出适当的推论。

想要检验统计上假设的正确性的为零假设（Null Hypothesis，记为H0），零假设通常由研究者决定，反映研究者对位置参数的看法。

相对于零假设的其他有关参数的论述为被备择假设（Alternative Hypothesis，记为Ha或H1），它通常反映了执行检验的研究者对参数可能数值的另一种（独立的）看法，换句话说，备择假设通常才是研究者最想证明的（反证法的本质逻辑）。

参考：https://zh.wikipedia.org/zh-cn/%E5%81%87%E8%AA%AA%E6%AA%A2%E5%AE%9A

⚠️ 特别注意：

本篇博客只讨论参数检验与非参数检验，至于什么时候需要参数检验、什么时候需要非参数检验，

什么时候可以对数据进行基本转换处理来避免非参数检验，

以及各种假设检验在少样本、大样本，或者其他特殊情况下的校正、近似处理严谨与否等等，都没有深入地讨论。

本文最初比较的想法，参考自一篇简单文献：https://pmc.ncbi.nlm.nih.gov/articles/PMC4754273/，文献本身参考价值不大，但是对几个基本的假设检验的过程举例倒是通俗易通，本文中截图部分就是参考。

但不局限于文献中提及到的几种基本假设检验，更不用说其余大篇幅的发散思考了，

⚠️ 总之形式意义大于严谨性方面，仅供作为大纲发散参考

一，参数检验

参数检验是一种统计学方法，用于检验一个或多个总体参数的假设。

在统计学中，总体参数通常指的是总体的均值、方差、比例等。

参数检验的目的是根据从总体中抽取的样本数据，对总体参数的假设进行检验，以确定这些假设是否能够在统计上得到支持或拒绝。

1，参数检验的特点：

• 分布假设：进行参数检验前，通常需要假设数据来自特定的分布，最常见的假设是数据呈正态分布。
• 参数依赖：检验的焦点是总体的参数，如均值、方差等。
• 样本数据：虽然参数检验对数据分布有假设，但它通过样本数据来进行推断和分析，旨在基于样本统计量来估计或检验总体参数。

2，常见的参数检验：

• 分布假设：进行参数检验前，通常需要假设数据
• 来自特定的分布，最常见的假设是数据呈正态分布。
• 参数依赖：检验的焦点是总体的参数，如均值、方差等。
• 样本数据：虽然参数检验对数据分布有假设，但它通过样本数据来进行推断和分析，旨在基于样本统计量来估计或检验总体参数。

3，参数检验的使用条件：

• 数据必须来自于一个或多个已知分布的总体，最常见的是正态分布（正态总体）。
• 样本数据应随机抽取，且样本间相互独立（样本独立）。
• 根据不同的检验方法，可能还需要满足方差齐性（即各组数据的方差相等）的条件（方差齐性）。

二，非参数检验

非参数检验是统计学中一类不依赖于数据分布假设的检验方法。

与参数检验不同，非参数检验不需要假设数据来自特定的分布（如正态分布），因此它们在应用时更加灵活，特别适合于处理不满足正态分布或分布未知的数据。非参数检验主要基于数据的顺序或排名，而不是确切的数值，从而允许它们对数据的中位数、分布形态或变异性进行推断。

1，非参数检验的特点

• 无需分布假设：最大的特点是不依赖于被检验数据的分布形式，使得它在处理不符合正态分布的数据时特别有用。
• 适用范围广：可以用于连续数据、有序分类数据及名义分类数据。
• 基于排名或分类：许多非参数检验方法是基于数据的排名（rank，也就是秩）或分类（classification）而不是原始数值（value）进行的，这减少了异常值的影响。
• 灵活性：适用于样本量小的情况，以及数据收集标准不允许精确测量的场景。

2，常见的非参数检验

• 曼-惠特尼U检验（Mann-Whitney U test）：用于比较两个独立样本的中位数是否存在显著差异。
• 威尔科克森符号秩检验（Wilcoxon signed-rank test）：用于比较两个相关样本、匹配样本或成对样本的差异。
• 克鲁斯卡尔-沃利斯检验（Kruskal-Wallis H test）：是曼-惠特尼U检验在三个或多个独立样本情况下的推广，用于比较它们的中位数是否相同。
• 卡方检验（Chi-square test）：用于比较实际观察频数和理论期望频数之间的差异，适用于名义分类数据的分析。

3，非参数检验的适用条件

• 当数据不符合正态分布或者分布未知时。
• 样本量较小，难以准确估计总体分布时。
• 在处理有序分类数据或名义分类数据时。
• 当数据中存在异常值或数据范围受限时。

4，非参数检验的优缺点

（1）优点

• 由于不需要对总体进行假设，因此得出错误结论的可能性较小。换句话说，这是一种保守的方法
• 更直观是，且不需要太多统计学知识
• 统计计算基于符号或顺序/秩，因此受异常值的影响不大
• 甚至适用于小样本

（2）缺点

• 由于无法确定分布函数，因此无法知道总体中的实际差异
• 与参数方法相比，非参数方法获得信息有限，且更难解释
• 与非参数方法相比，分析方法只有少数几种
• 数据中的信息没有得到充分利用
• 对于大样本，计算变得复杂

三，配对的参数检验与非参数检验

总是有效，但并不总是高效 vs 总是高效，但并不总是有效

1，参数检验 vs 非参数检验

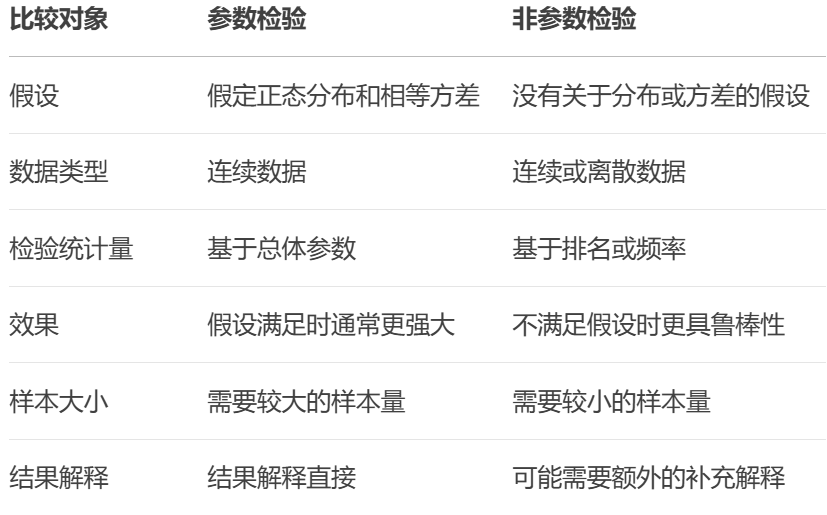
数据本身的值（value） vs 数据的符号（sign）和顺序（rank，秩）

强调均值差异 vs 强调中位数差异

（1）假设条件：

• 参数检验假设总体数据服从特定的参数化分布，例如正态分布、二项分布等，并且对总体参数（如均值、方差）的数值进行假设检验。
• 非参数检验不对总体数据的分布做出特定的假设，通常是基于数据的秩次（rank，排序）或频次进行推断，因此对总体参数的分布形式没有要求。

（2）数据类型：

• 参数检验通常适用于连续型数据，或者当样本容量较大时，对分类型数据也可以进行参数检验。
• 非参数检验更加灵活，适用于各种类型的数据，包括连续型、分类型、顺序型等。

（3）数据要求：

• 参数检验通常适用于连续型数据，或者当样本容量较大时，对分类型数据也可以进行参数检验。
• 非参数检验更加灵活，适用于各种类型的数据，包括连续型、分类型、顺序型等。

（4）检验效果：

• 在总体满足参数假设的情况下，参数检验通常更强大（即更容易发现真实存在的差异）。
• 当总体分布未知或不满足参数假设时，非参数检验可以提供一种更具有鲁棒性的检验方法。
• 总的来说，使用非参数分析方法可以降低得出错误结论的风险，因为这些方法不对总体作出任何假设，而可能具有较低的统计功效。换句话说，非参数方法是“总是有效，但并不总是高效”；而参数方法是“总是高效，但并不总是有效”。因此，当参数方法确实适用时，建议使用参数方法。

（5）假设差异：

• 数据本身的值（value） vs 数据的符号（sign）和顺序（rank，秩）
• 强调均值差异 vs 强调中位数差异

我们知道样本均值其实是很容易受极端值的存在影响的，而中位数则抗noise能力强，也就是中位数是一个更稳健的指标来描述数据的中心位置。中位数不受极端值的影响，能够更好地反映数据的典型水平。

• 对数据分布的假设：
  • 参数检验：假设数据服从特定的分布，通常是正态分布。在这种假设下，均值是描述数据集中趋势的一个很好的指标，因为它能够充分利用数据的所有信息，并且在正态分布的情况下，均值和中位数是相等的。
  • 非参数检验：不假设数据服从特定的分布。当数据分布未知或不满足正态性假设时，中位数是一个更稳健的指标来描述数据的中心位置。中位数不受极端值的影响，能够更好地反映数据的典型水平。
• 对异常值的敏感性：
  • 参数检验：均值对异常值非常敏感。一个极端的观测值会显著影响均值的大小，从而可能导致对数据集中趋势的误判。
  • 非参数检验：中位数对异常值具有很强的抗性。无论数据中是否存在极端值，中位数都能保持稳定，因此在数据存在异常值或分布偏斜时，非参数检验更能准确地反映数据的真实情况。
• 数据的利用方式：
  • 参数检验：利用数据的具体数值进行计算，通过计算均值、标准差等统计量来评估数据的分布情况和差异程度。
  • 非参数检验：主要基于数据的秩或符号进行分析，不依赖于数据的具体数值，而是关注数据的相对大小顺序。这种方法在一定程度上简化了计算，但也可能导致部分信息的丢失。

联系

• 在正态分布下的等价性：当数据服从正态分布时，均值和中位数是相等的，此时参数检验和非参数检验的结果通常会非常接近。在这种情况下，两种检验方法都可以有效地检验数据的中心位置是否存在差异。
• 都是对数据集中趋势的度量：无论是均值还是中位数，它们都是用来描述数据集中趋势的统计量。虽然它们在计算方式和对数据的敏感性上有所不同，但它们的目的都是为了帮助我们了解数据的典型水平或中心位置。

例如

假设我们有一组数据，表示某个班级学生的考试成绩（满分100分）：90、92、95、98、100、100、100、100、100、100。这组数据的均值为97.8，中位数为100。从均值来看，这个班级的成绩似乎很高，但中位数更能反映大多数学生的实际成绩水平。如果我们在分析时只关注均值，可能会高估班级的整体成绩水平。而中位数则更直观地告诉我们，有一半以上的学生的成绩达到了100分。

再假设我们有另一组数据，表示某个班级学生的考试成绩（满分100分）：50、60、70、80、90、100、1000。这组数据的均值为157.14，中位数为80。由于存在一个极端的异常值（1000分），均值被严重拉高，无法真实反映班级的典型成绩水平。而中位数则不受这个异常值的影响，能够更准确地表示大多数学生的成绩集中在80分左右。

通过这两个例子可以看出，当数据分布较为均匀且没有极端值时，均值和中位数都能较好地反映数据的集中趋势；但当数据存在极端值或分布偏斜时，中位数比均值更能准确地描述数据的典型水平。这也是为什么非参数检验通常检验中位数，而参数检验通常检验均值的原因（涉及到我们对于总体分布的先验知识）。

2，对应版本 vs

from scipy import stats

同时提供python库中的基础实现，api调用

1. 单样本位置检验（与某个理论值比较）

单样本均值检验 vs 单样本中位数检验

检验场景	方法名称	定义与目的	前提条件	原假设 (H₀) vs. 备择假设 (H₁)	检验统计量
参数版本	单样本 t 检验 (scipy.stats.ttest_1samp)	检验单个总体的均值是否等于某个理论值。 用于比较一个样本的均值是否与已知的总体均值或理论值有显著差异。 + 示例：你想知道一群学生的平均考试成绩是否显著高于全国平均分（已知的总体均值）。	1. 数据连续。 2. 数据独立抽样获得。 3. 数据近似服从正态分布（尤其在小样本时重要）。 注意这里没有强调方差齐性的前提，因为它比较的是一组样本的均值与一个已知的总体均值的差异，而方差齐性的概念在这里不适用，因为只有一个样本，所以单样本t检验我们不强调方差齐性（不需要满足，也别和后面其他的t检验混淆）	H₀: 总体均值 μ = μ₀ H₁: μ ≠ μ₀ (双侧) 或 μ >/< μ₀ (单侧)	t 统计量：
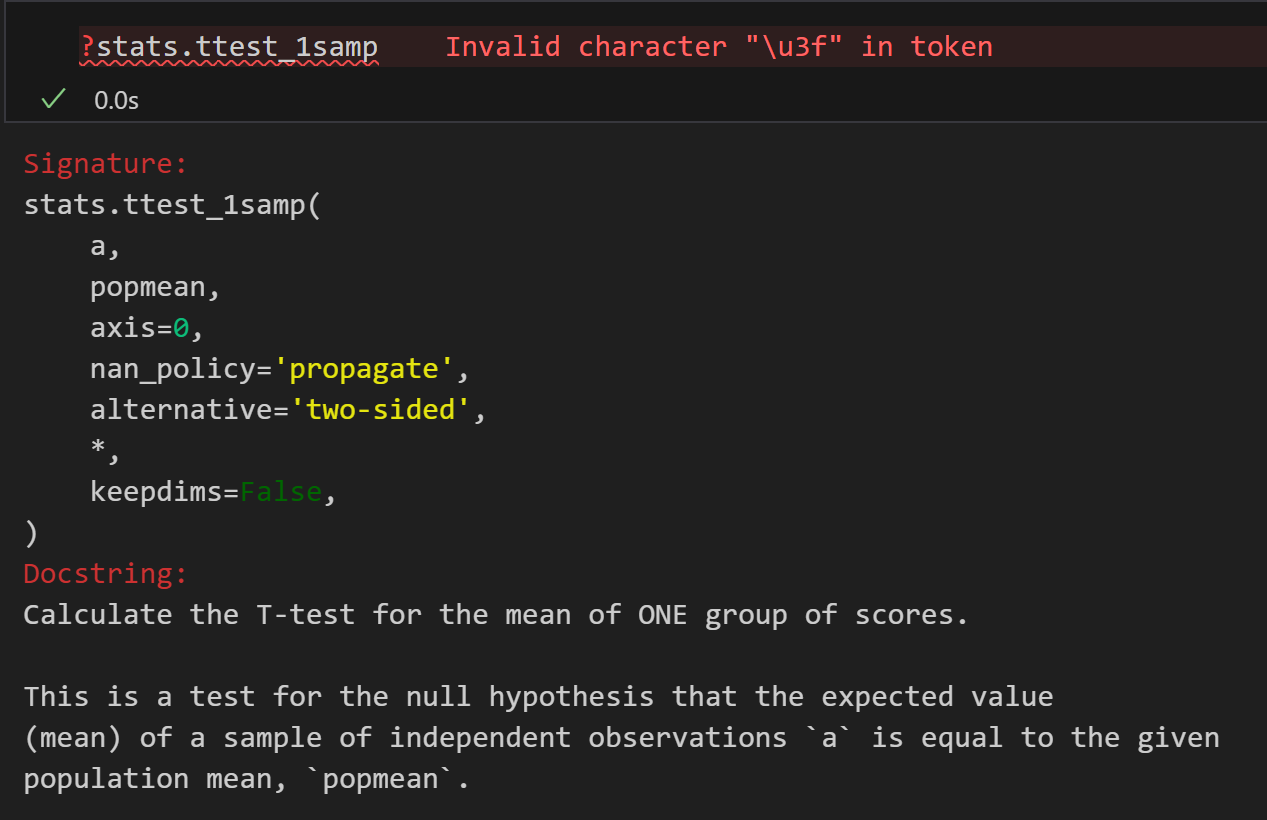
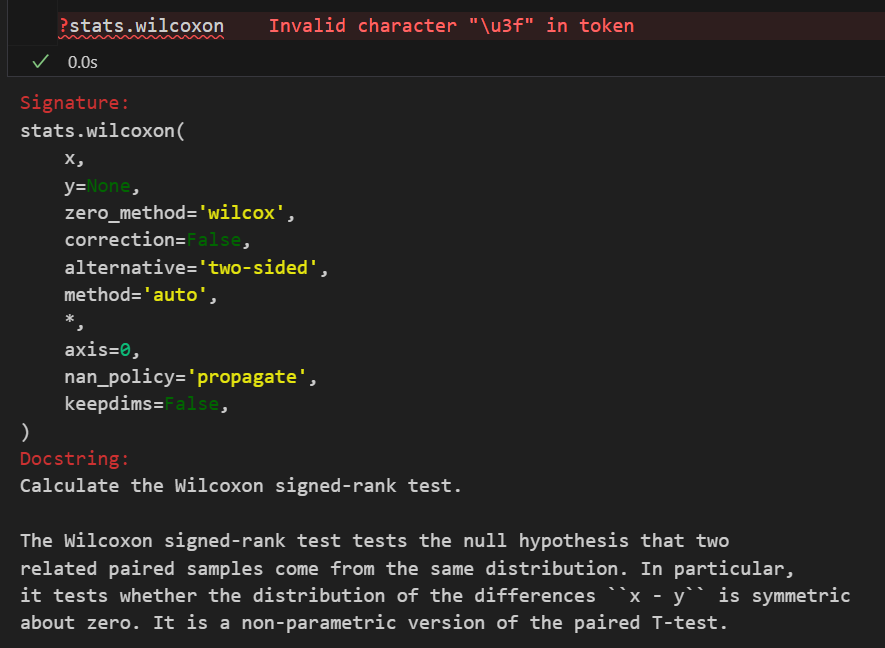
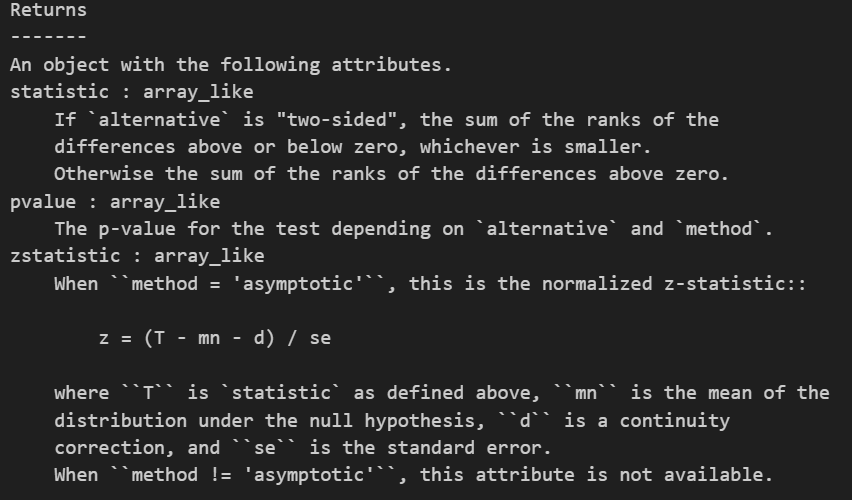
非参数版本	符号检验（Sign test）/ Wilcoxon 符号秩检验（Wilcoxon signed-rank test） (scipy.stats.wilcoxon)	检验单个总体的中位数是否等于某个理论值。符号秩检验比单纯的符号检验更强大。	1. 数据连续或顺序。 2. 数据独立抽样获得。 3. 无需数据服从正态分布。	H₀: 总体中位数 M = M₀ H₁: M ≠ M₀ (双侧) 或 M >/< M₀ (单侧)	Wilcoxon 符号秩统计量： 基于数据与理论值之差的绝对值的秩次之和。

---

符号检验（Sign Test）

1. 定义

符号检验是非参数检验中关于样本位置的最简检验方法。

2. 目的

3. 检验步骤

(1) 数据标记

(2) 计算符号统计量

(3) 样本调整

4. 假设检验

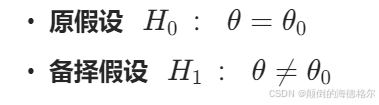
5. 检验统计量

6. 检验决策

7. 特点

• 非参数性：不依赖数据分布假设，仅使用符号（+ / -）进行分析；
• 适用性：特别适用于数据难以测量或分布未知的情形。

数学表示

• 

---

Wilcoxon 符号秩检验（Wilcoxon’s Signed Rank Test）

1. 目的

2. 与符号检验的对比

符号检验（Sign Test）

Wilcoxon 符号秩检验

3. 计算步骤

4. 示例

总的来说，Wilcoxon 符号秩检验通过考虑数据的相对大小（排名）来弥补符号检验的不足，从而具有更高的统计功效。

---

我们还是用下面这组数字作为例子进行分析：

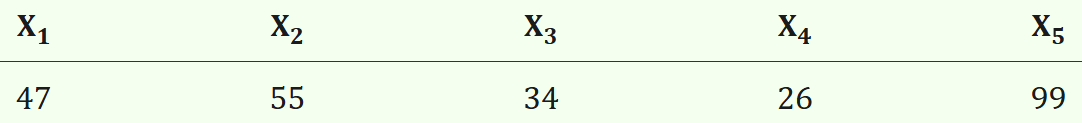
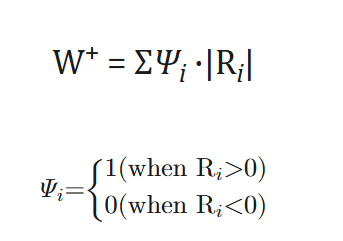
我们可以发现，signed rank test相比较sign test，其实就是检验量对sign的简单频数用rank进行了加权，计算的同样还是+号的样本。

2. 两独立样本比较（不同组别间比较）

检验场景	方法名称	定义与目的	前提条件	原假设 (H₀) vs. 备择假设 (H₁)	检验统计量
参数版本	独立样本 t 检验 (scipy.stats.ttest_ind)	比较两个独立总体的均值是否存在差异。	1. 数据连续。 2. 两组数据独立。 3. 两组数据近似服从正态分布。 4. 两组数据方差齐性（方差相等）。 注意，因为这里要比较的是两个不同的样本，所以一般来说需要确保两个样本所来自的总体的方差相等，也就是方差齐性。 但是理论方面，方差不等（其余条件还是满足的话），还是可以使用t检验的，即Welch t-test。 所以我们一般说的数据独立性、正态总体、方差齐性，这3个耳熟能详、应该满足的基本条件，其实第一次接触就是在这里的独立样本t检验中接触到的。	H₀: 总体1均值 μ₁ = 总体2均值 μ₂ H₁: μ₁ ≠ μ₂ (双侧) 或 μ₁ >/< μ₂ (单侧)	t 统计量： 根据方差是否齐性使用不同的公式（从统计量角度来看，分子上的均值差是不变的，方差齐性与否的版本，差异在于分母上的标准误公式进行了校正），综合了均值差和合并标准误。
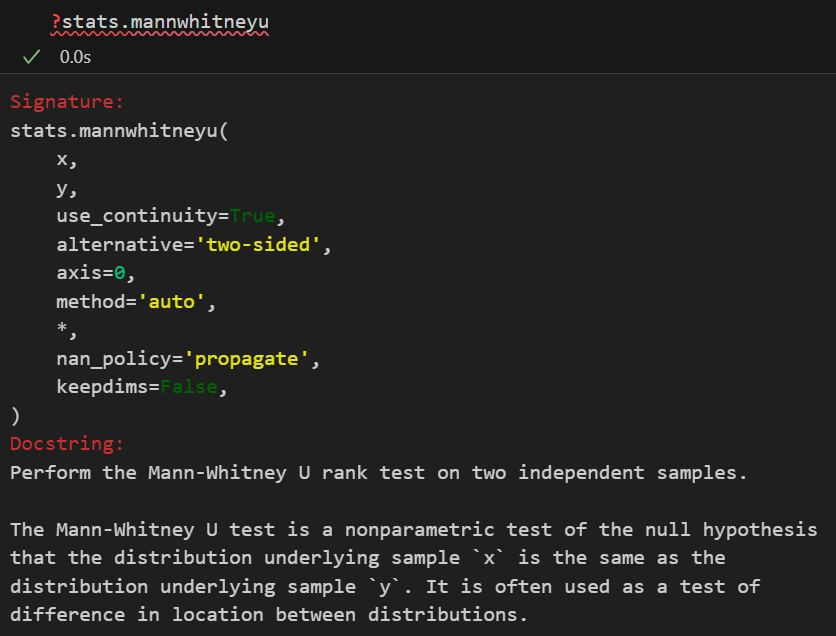
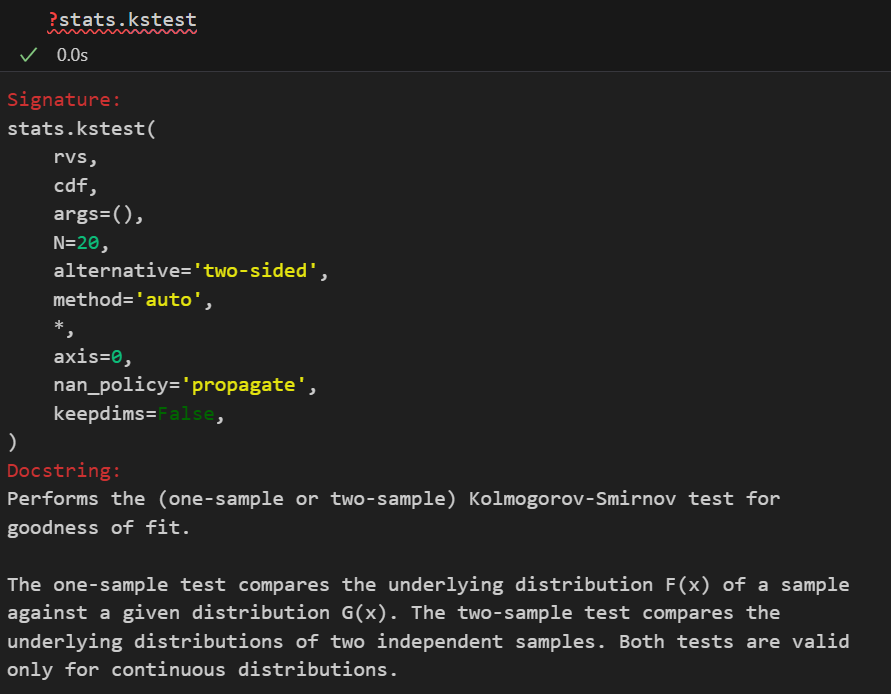
非参数版本	威尔科克森秩和检验（Wilcoxon’s Rank Sum Test）(scipy.stats.ranksums)/曼-惠特尼 U 检验 （Mann-Whitney test） (scipy.stats.mannwhitneyu)/Kolmogorov-Smirnov检验 (scipy.stats.kstest)	比较两个独立总体的分布是否存在差异（通常理解为比较中位数）。 如果要更加严格、全面地比较两个分布（的形状）是否存在差异，参考下面的K-S检验，也就是Kolmogorov-Smirnov检验	1. 数据连续或顺序。 2. 两组数据独立。 3. 无需正态性和方差齐性。	H₀: 两总体的分布相同 H₁: 两总体的分布不同（或一方随机大于另一方） 可以代入中位数比较、非中位数比较去理解	U 统计量： 将两组数据混合排序后，基于一组的秩次之和计算得出。

---

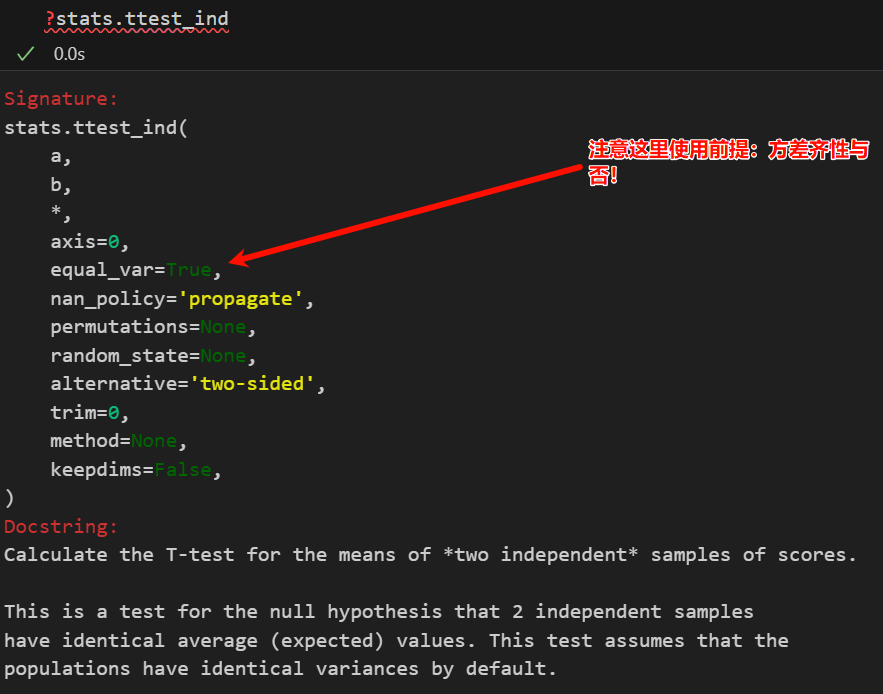
equal_var参数可以选择方差齐性与否的假设前提，

理论方面就不多说了，可以参考我之前的一遍博客：https://blog.csdn.net/weixin_62528784/article/details/148953343?spm=1001.2014.3001.5502；当然，据我了解，基本上本科生学概率统计学到t检验这一块很多变体都会介绍，所以Welch t-test这里就不过多废话了。

可以参考维基：https://en.wikipedia.org/wiki/Welch%27s_t-test

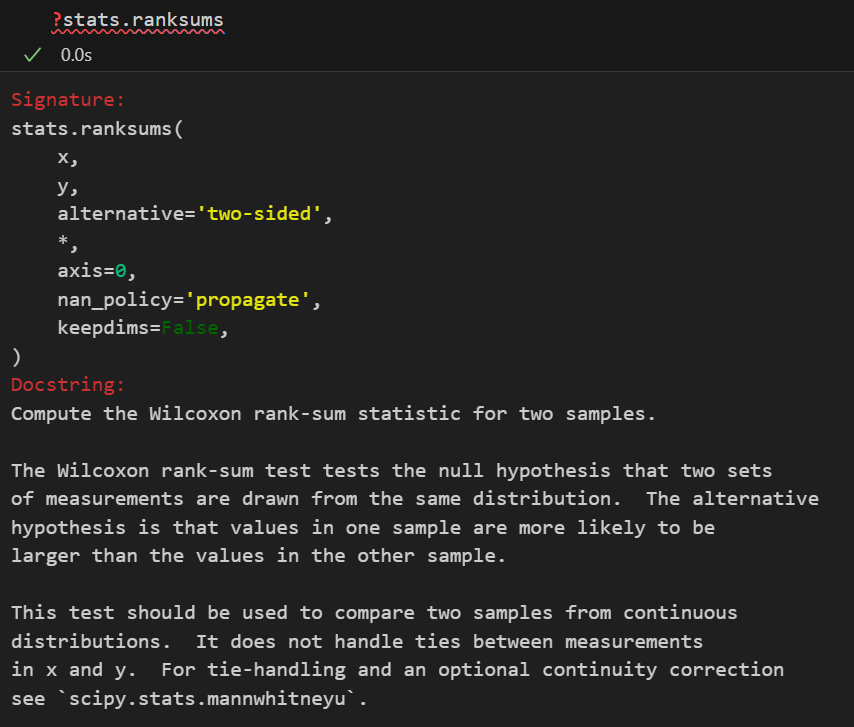
Wilcoxon秩和检验（Wilcoxon’s Rank Sum Test）

示例

Mann-Whitney U检验（Mann-Whitney Test）

• 数据比较：
  

• 计算U统计量：
  

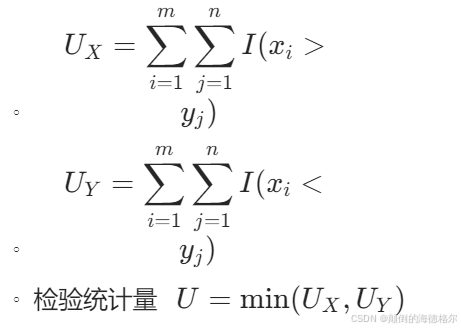
• 检验统计量的期望值：
  

• 临界值与P值：

  • 根据U检验的临界值表，确定在给定显著性水平下的临界值
  • 如果计算出的U值小于临界值，则拒绝原假设；否则，不能拒绝原假设

示例

Kolmogorov-Smirnov检验（K-S Test）

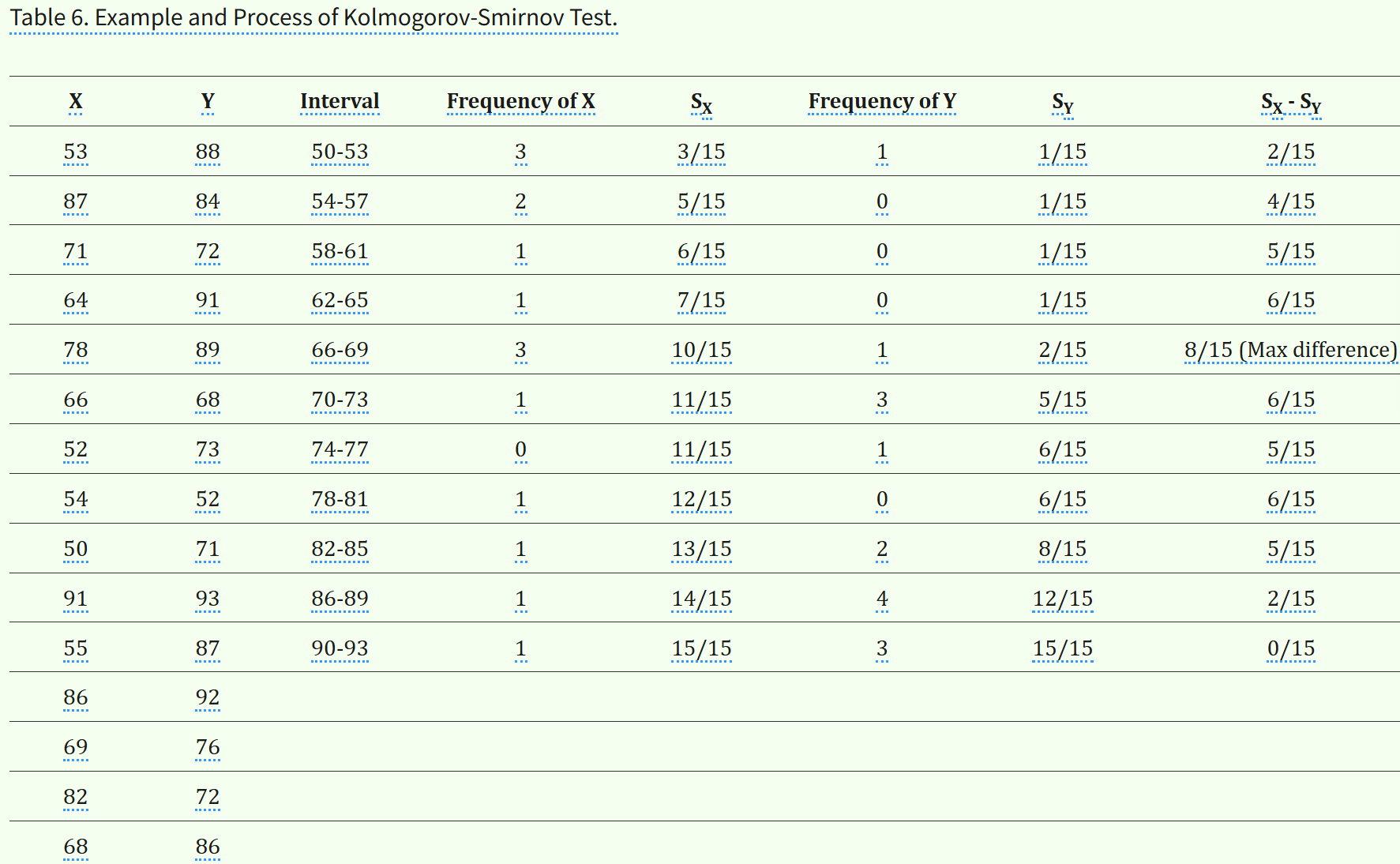
示例

方法总结与比较

检验方法	检验目标	主要统计量	适用条件
Wilcoxon秩和检验	比较两个样本的中心位置差异	秩和W	两个独立样本，至少有序尺度
Mann-Whitney U检验	比较两个样本的中心位置差异	U统计量	两个独立样本，至少有序尺度
Kolmogorov-Smirnov检验	比较两个样本的分布形状差异	最大差异值D	两个独立样本，连续变量

选择

• 当关注中心位置差异时，选择Wilcoxon秩和检验或Mann-Whitney U检验
• 当关注整体分布形状差异时，选择Kolmogorov-Smirnov检验
• 对于大样本情况，Mann-Whitney U检验和Wilcoxon秩和检验是等价的
• K-S检验对任何分布差异都敏感，但需要较大的样本量来获得足够的检验效能

这里再重申一下，相比Wilcoxon秩和检验（Mann-Whitney U检验），K-S检验比较的是分布形状而不是中心位置，

前者

• 目的：主要用来比较两个独立样本的中心位置（中位数或均值）是否存在显著差异。
• 原理：
  • Wilcoxon秩和检验：通过计算两个样本的秩和来判断两个样本的中心位置是否相同。如果两个样本来自同一分布，它们的秩和应该接近某个理论值。
  • Mann-Whitney U检验：通过计算一个样本中的数据大于另一个样本中数据的次数来判断两个样本的中心位置是否相同。如果两个样本来自同一分布，那么一个样本中的数据大于另一个样本中数据的概率应该是1/2。

后者

• 目的：主要用来比较两个独立样本的整体分布是否存在显著差异，而不仅仅是中心位置。
• 原理：
  • 累积分布函数（CDF）：K-S检验的核心是累积分布函数（CDF）。累积分布函数表示数据小于或等于某个值的概率。如果两个样本来自同一分布，它们的累积分布函数应该是相同的。
  • 最大差异：K-S检验通过计算两个样本的累积分布函数之间的最大差异（即最大绝对差值）来判断两个样本是否来自同一分布。如果这个最大差异超过了某个临界值，就可以拒绝原假设，认为两个样本来自不同的分布。

前2个检验主要关注的是两个样本的中心位置（中位数或均值）。它们假设数据的分布形状是相似的，只是中心位置可能不同。

而K-S检验则更全面，它不仅考虑中心位置，还考虑了整个分布的形状。这意味着它能够检测到两个样本在分布形状上的差异，而不仅仅是中心位置的差异。

至于分布形状上，能够检查的方面就更多了，偏斜度、峭度等等等等。

---

K-S检验与PP图、QQ图

这里需要提一下的是K-S检验的发散，我们再看看原理：

• 原理：K-S检验主要用于检验数据集的正态性，但其最初是用于检验两个独立样本的累积分布函数是否相同，以此判断这两个样本是否来自具有相同分布的总体或同一总体。如果两个样本来自同一总体，它们的累积分布形状应相同；若累积分布不同，则可认为它们来自不同的总体。
• 进行K-S检验时，需要先确定两个样本的分布模式，然后计算每个区间内两个样本的累积概率分布，并找出两者累积分布的最大差异值，该最大差异值即为检验统计量。将该统计量与临界值比较，即可判断两个样本是否同质。

其实涉及到样本的经验分布与理论分布的比较，本质上方法都是通用的，我们很快就能够想到t检验使用前提中，判断总体分布的正态性时，涉及到P-P图（Probability-Probability Plot）和Q-Q图（Quantile-Quantile Plot）那一部分的知识。

我们都知道，P-P 图和Q-Q 图是两种用于检验数据分布是否符合某种理论分布的简单可视化方法，而且一般都用于正态分布的检验。

1. Kolmogorov-Smirnov (K-S) 检验

原理

K-S检验是一种非参数检验方法，用于：

• 比较一个样本的经验分布函数与理论分布函数是否一致
• 比较两个样本的经验分布函数是否相同

计算步骤

应用场景

• 判断单个样本是否来自某一理论分布（如正态分布）
• 比较两个样本是否来自同一分布

特点

• 数值化检验方法，提供严格的统计显著性判断
• 适用于样本量较大的情况
• 对分布的整体形状敏感，但对分布的尾部敏感度较低

2. P-P图（Probability-Probability Plot）

参考：https://en.wikipedia.org/wiki/P%E2%80%93P_plot

原理

P-P图是一种图形化方法，用于比较样本的经验分布函数与理论分布函数

绘制步骤

应用场景

• 判断样本是否来自某一理论分布
• 直观评估样本分布与理论分布的拟合程度

特点

• 图形化方法，直观易懂
• 对分布的整体形状敏感
• 对分布的尾部敏感度较低
• 适合直观判断，但缺乏严格的统计显著性判断

3. Q-Q图（Quantile-Quantile Plot）

参考https://en.wikipedia.org/wiki/Q%E2%80%93Q_plot

原理

Q-Q图是一种图形化方法，用于比较样本的分位数与理论分布的分位数

绘制步骤

应用场景

• 判断样本是否来自某一理论分布
• 直观评估样本分布与理论分布的拟合程度

特点

• 图形化方法，直观易懂
• 对分布的尾部敏感度较高，能够更好地检测分布的尾部差异
• 适合直观判断，但缺乏严格的统计显著性判断

4. 方法比较与联系

共同点

• 三者都可以用于判断数据的分布特性，包括正态性
• 都是基于样本的经验分布与理论分布的比较

区别与选择指南

方法	类型	敏感度	适用场景	优缺点
K-S检验	数值检验	整体形状敏感	需要严格统计判断，大样本情况	提供统计显著性，但对尾部不敏感
P-P图	图形方法	整体形状敏感	直观评估整体拟合程度	直观易懂，但缺乏统计检验
Q-Q图	图形方法	尾部高度敏感	检测尾部差异，直观评估	对尾部敏感，但缺乏统计检验

总的来说，P-P图用于快速的可视化检查，需要直观评估整体拟合；

Q-Q图差不多，对极端值更敏感，需要检测分布尾部差异；

真正要做严格的统计判断时，还是要依赖K-S检验，也比较适用于样本量较大的情况。

而且大多数人在做大样本数据相关的假设检验时，其实绘制直方图、或者通过一些对数log变换，观察shift之后的直方图，本质上也只是一种粗略地、经验地检查正态理论分布的方法。逻辑上其实和这里的PP/QQ/KS是一致的，只不过经验地转换为理论的、直观的转换为程序化的检查操作与流程。

其实说到这里，既然已经提及了两个概率分布之间的差异，其实我们更容易想到的是在机器学习、深度学习中的应用，我们在构建loss损失函数的时候。

比如说GAN、VAE、Diffusion等模型，我们涉及到要衡量两个分布之间的差异时。

我遇到过一个学生，同时修机器学习入门和统计学习，问过一个问题“既然KS检验是找两个概率分布函数之间最大的分离，而KL散度是看两个概率分布函数之间总体的差异，那么它们两个能够互换使用吗，或者作为一种测试的伪方法？”

这里要深究还确实有点关系，

我们常用的用于描述或者是衡量两个概率分布之间的差异，的方法，

经典的比如说 Kullback-Leibler (KL) 散度、Jensen-Shannon 距离（本质就是KL散度的一种对称版本）等。

以KL散度为例，有一些特殊情况（例如，某些似然比检验），其中K-S检验统计量可以被证明与KL散度有关。

但总的来说，如果我们想要围绕散度设计一个检验（也许同样是在经验分布和特定的原假设分布之间），我们要做的工作可能会很多。比如说，需要推导出在原假设下散度的分布，并证明我们的检验与已经存在的检验相比具有可接受的功效等，或者直接基于样本散度统计量进行置换检验或自助法bootstrap检验。

简而言之，KL散度和K-S检验不能够互换使用，因为它们描述的是完全不同的东西。

将所有的数据拉出来排个序，注意数据来源于哪个样本（总体）。

表格中数据的比对逻辑如下：

比如说Number of X＞Y，就是固定这个X，对于Y中的每个数据，这个X大于多少个Y中的数据（就是fix这个X，然后loop through Y，然后看看这个X比多少个Y大）；

比如说X=18，就大于Y中的11、16、14一共是3个数；

X=21，多了个20大于；

同理X=15，就大于其中的11、14；

X=30、25和21一样，大于所有Y中的4个数。

然后所有的比较一共有20次，其实就是两两比较有20次（C10,2）。

然后按照零假设的话，两组中任意一组的值比较应该有大有小，也就是理想的20次比较中，比如说大于或者小于，总之单侧是10。

K-S检验受其设置的分布区间划分间隔影响：首先样本数据值X、Y的值域区间都是明确的（min、max、分位数区间等基本统计参数确定），这个区间是不会变的。

然后就是看所设置的间隔了，区间大小是固定的，那么划分的频数间隔过大（too wide），则划分出来的间隔区间数就越少，那么数据点落在区间内的频率就会增大，两个样本的频数分布之间就分不太开，统计功效就会减弱。

反之，划分频数间隔过小（too narrow），那么划分出来的区间间隔数目就会越多，频数计算就会越复杂。

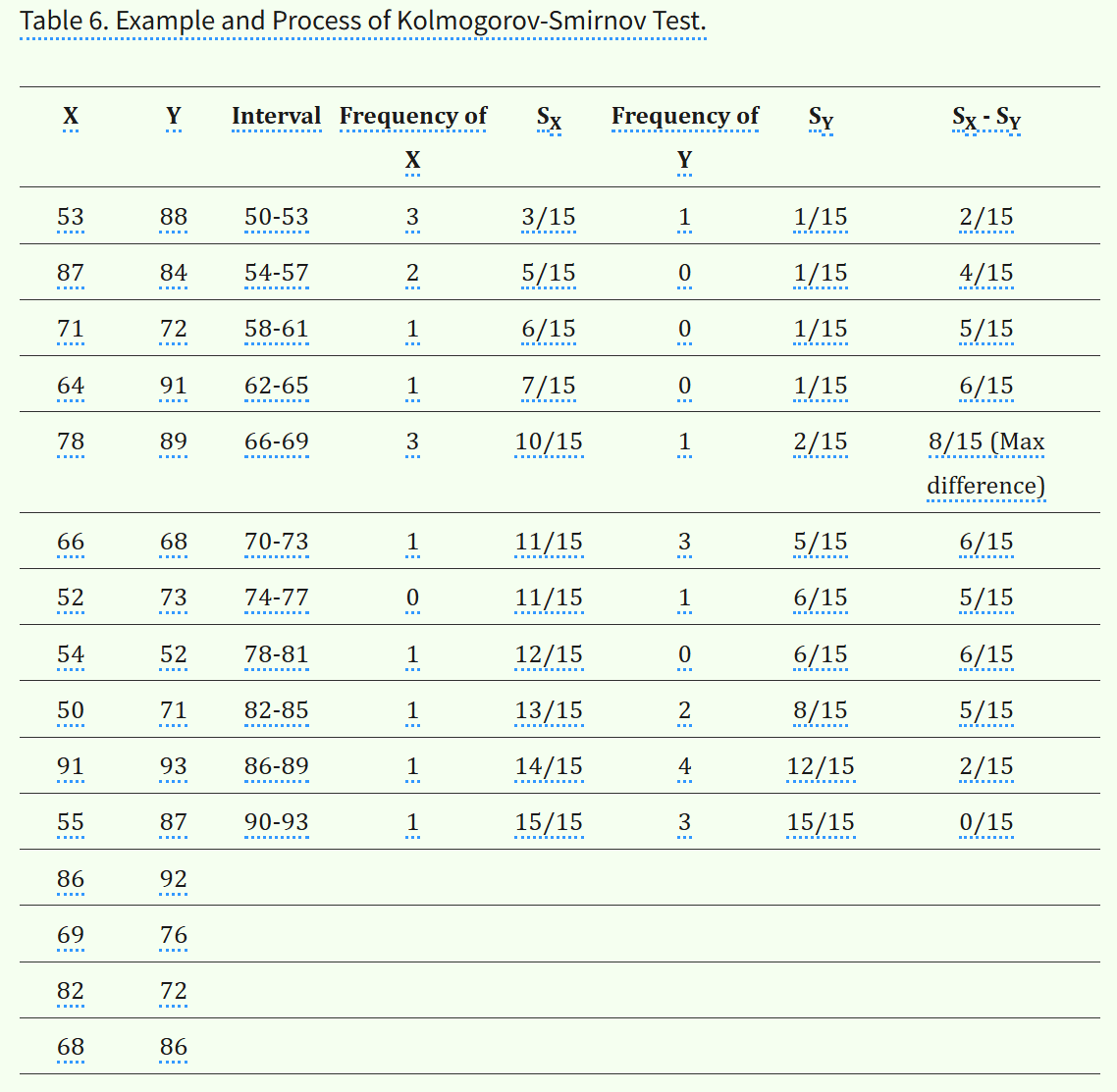
区间为50-93，间隔43；

设置区间间隔为4，则有11个区间。

用频数-频率分布，也就是经验分布，来评估概率分布。

这个最大频率差就是要检验的统计量，至于参考值，这些非参数检验基本都是查表（一定置信度下的统计量边界值），当然程序中都内置了。

3. 两配对样本比较（同一对象前后比较，比较随时间变化同一对象的两个测量值）

用于比较同一组样本在两个不同条件下的均值/中位数差异，而这些条件是相关的；

本质上，配对样本t检验及其非参数版本只是对每个配对样本的差异进行单样本t检验及其非参数版本。

检验场景	方法名称	定义与目的	前提条件	原假设 (H₀) vs. 备择假设 (H₁)	检验统计量
参数版本	配对样本 t 检验 (scipy.stats.ttest_rel)	比较同一组对象在两种不同条件下的均值是否存在差异。	1. 数据连续。 2. 两组数据配对（非独立）。 3. 差值（d = x₁ - x₂）近似服从正态分布。 注意，因为比较的实际上还是同一组样本/同一个对象，所以同样不需要满足方差齐性的前提条件。	H₀: 差值的总体均值 μ_d = 0 H₁: μ_d ≠ 0 (双侧) 或 μ_d >/< 0 (单侧)	t 统计量：
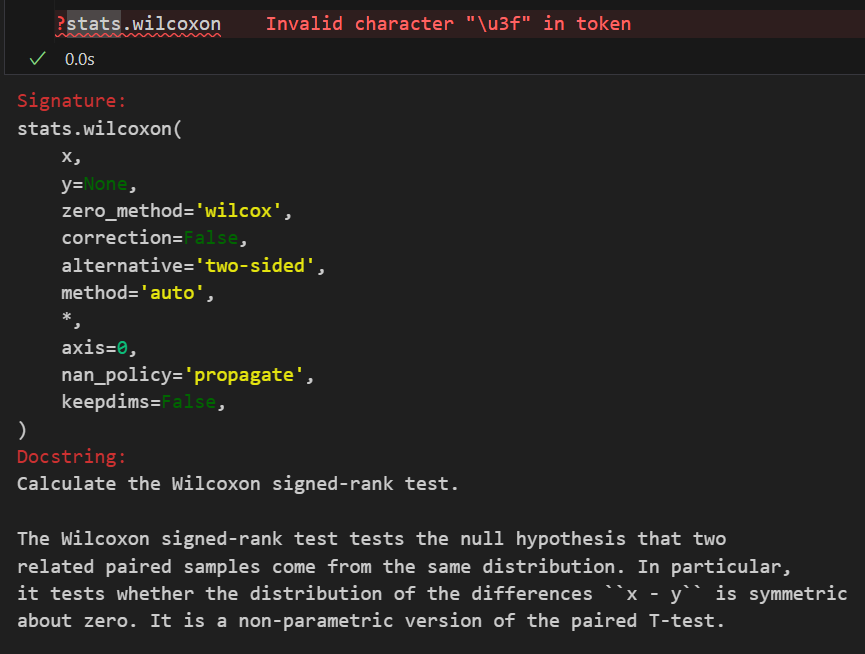
非参数版本	Wilcoxon 符号秩检验 (scipy.stats.wilcoxon)	比较同一组对象在两种不同条件下的中位数是否存在差异。	1. 数据连续或顺序。 2. 两组数据配对（非独立）。 3. 无需差值服从正态分布。	H₀: 差值的总体中位数 M_d = 0 H₁: M_d ≠ 0 (双侧) 或 M_d >/< 0 (单侧)	Wilcoxon 符号秩统计量： 基于差值绝对值的秩次之和。

---

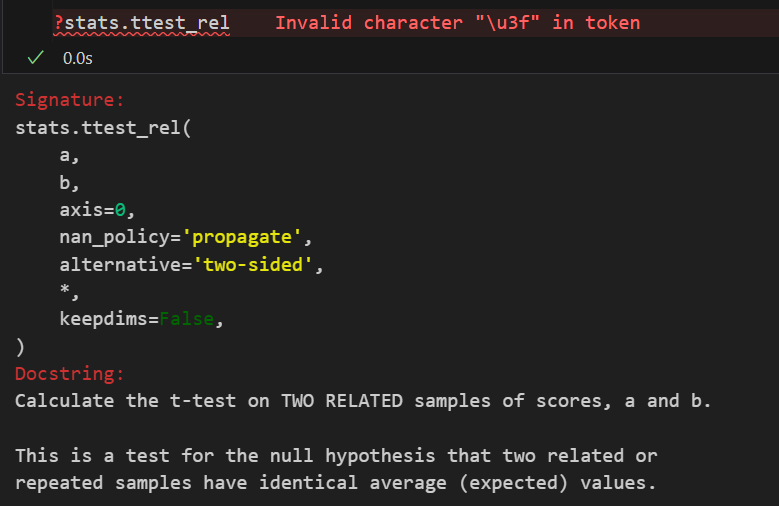
非参数版本的配对t检验，调用的api同样见前：

符号检验（Sign Test）

目的

比较配对样本处理前后的得分差异

方法

统计量

统计量为正号的数量（或负号的数量）

假设检验

局限性

• 只能提供差异的方向，不能提供差异的大小
• 不利用数据的大小信息，只关注符号

Wilcoxon’s Signed Rank Test

目的

比较配对样本处理前后的得分差异

方法

统计量

假设检验

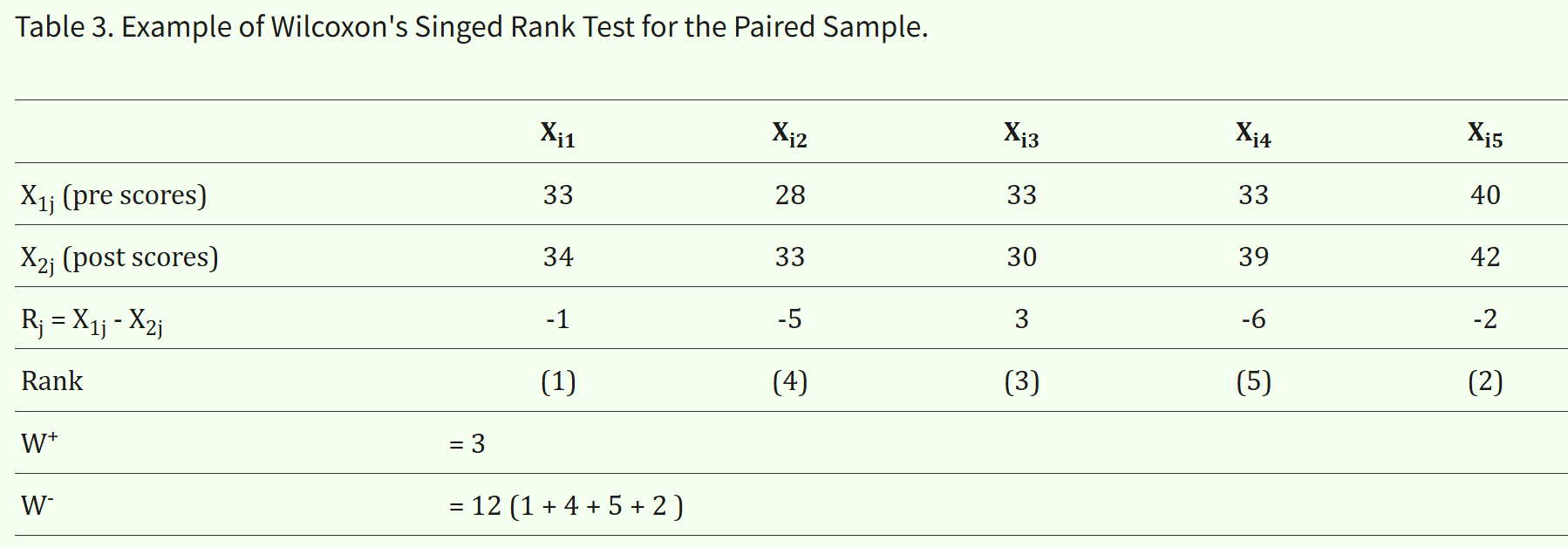
计算示例

给定5对样本数据：

前测得分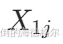	后测得分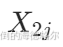	差值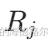	差值的绝对值排序	对应的秩次	符号
33	34	-1	1	(1)	-1
28	33	-5	2	(2)	-2
33	30	3	3	(3)	+3
33	39	-6	4	(4)	-4
40	42	-2	5	(5)	-5

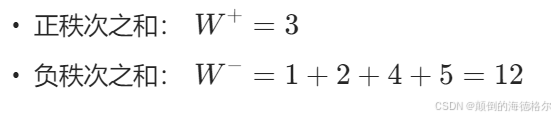
统计分析

优势

• 不仅考虑了变化的方向，还对变化的大小进行了排序
• 提供了更多的信息，因此统计功效更强

总的来说

符号检验

• 优点：对极端值不敏感
• 缺点：不能反映变化的大小，信息利用不充分

威尔科克森符号秩检验

• 优点：同时考虑了变化的方向和大小，统计功效更强
• 缺点：计算相对复杂，对数据的分布有一定的假设

这里其实和单样本t检验以及非参数版本对应起来，

单样本t检验以及非参数版本，是与预期的某个理论均值或者是中位数进行比较；

而配对数据，其实在做差值之后，比对的目的其实就很明确了，就是和0值进行比较，其实在做差值之后，获得单列的样本数据，就是按照单样本t检验以及非参数版本那一套进行了。

其实本质上来讲是，配对t检验只是对每个配对样本的差异进行单样本t检验，在这种情况下，原假设是配对样本差值为0。

另外检验的目的其实就很明确了，就是比较在配对实验或者是配对检查前后，对于指标变化的方向（direction）或者是变化的程度（degree）。

只考虑了变化的方向，就是只有sign的模糊位置信息；

进一步考虑了变化的程度，就是还有rank的相对大小信息。

4. 多组独立样本比较（方差分析）

检验场景	方法名称	定义与目的	前提条件	原假设 (H₀) vs. 备择假设 (H₁)	检验统计量
参数版本	单因素方差分析 (ANOVA) (scipy.stats.f_oneway)	比较三个及以上独立总体的均值是否存在至少一个与其他不同。	1. 数据连续。 2. 各组数据独立。 3. 各组数据近似服从正态分布。 4. 各组数据方差齐性。 注意，这里和两独立样本t检验一样，常规分析是3个条件都要满足，但是这里也有方差齐性不满足的welch版本的ANOVA	H₀: 所有总体均值均相等 (μ₁ = μ₂ = … = μk) H₁: 至少有两个总体均值不相等（不是所有总体均值都相等）	F 统计量：F值越大，越倾向于拒绝H₀。
非参数版本	克鲁斯卡尔-沃利斯 H 检验 (scipy.stats.kruskal)	比较三个及以上独立总体的分布是否存在差异（比较中位数）。	1. 数据连续或顺序。 2. 各组数据独立。 3. 无需正态性和方差齐性。	H₀: 所有总体的分布相同 H₁: 至少有一个总体的分布与其他不同	H 统计量： 基于所有数据混合排序后的秩次之和计算。
注意事后检验	post hoc test

---

同样的，方差齐性这里还有Welch版本，

参考维基：https://en.wikipedia.org/wiki/Analysis_of_variance

这会我们先按照我前面提到的那篇参考文献的例子来介绍，再解释：

Kruskal-Wallis 检验

目的

判断三个或更多独立样本的中位数是否存在差异

方法步骤

假设检验

Jonckheere 检验

目的

在已知各组之间存在某种顺序的情况下，检验这些组的中位数是否存在差异

假设（以上面表格中数据为例，3组为例）

方法步骤

1. 数据排序：将所有样本的数据合并，按从小到大的顺序排列
2. 计算秩次差异：
   

结论判断

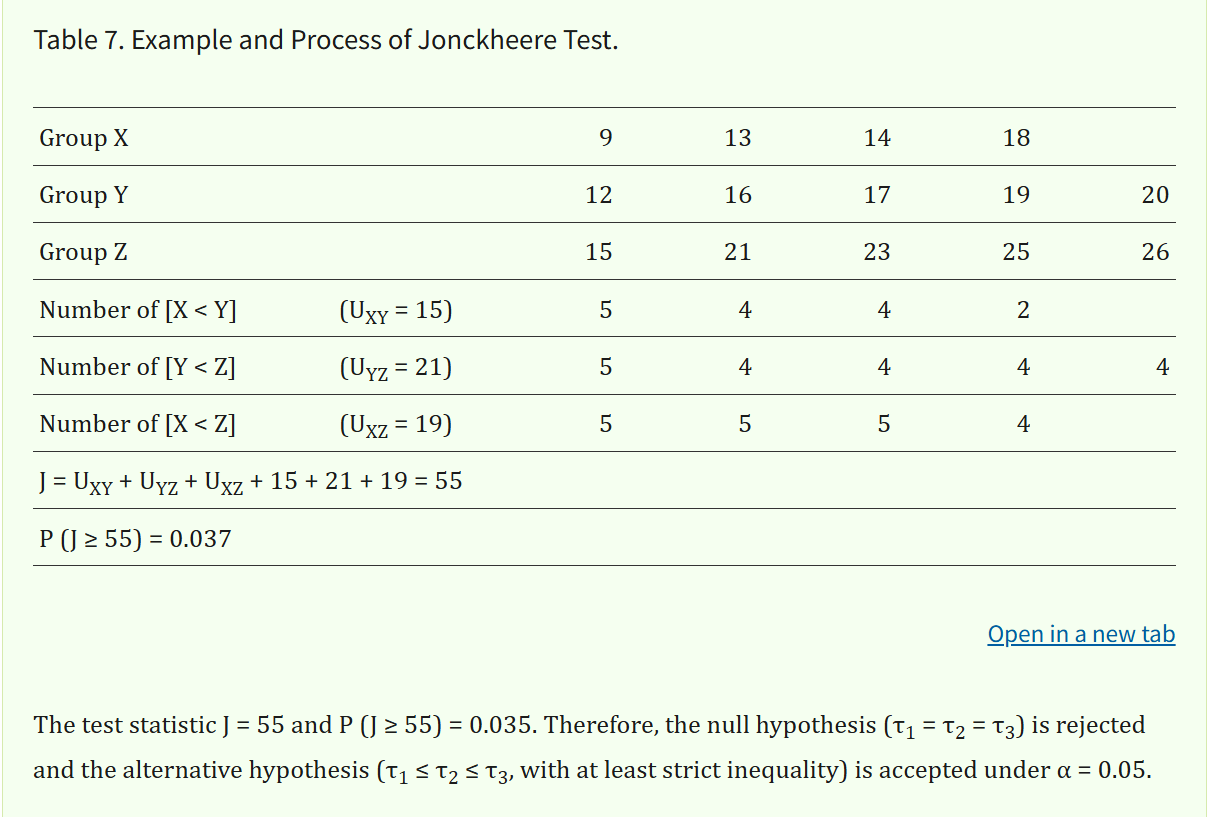
示例分析（以上面表格中3组为例）

数据

• 组 X：9、13、14、18
• 组 Y：12、16、17、19、20
• 组 Z：15、21、23、25、26

计算过程

计算统计量J

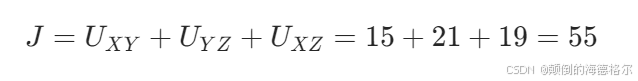
计算P值

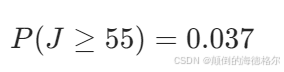
结论

方法比较与选择

检验方法	适用场景	假设条件	检验目标
Kruskal-Wallis	三组及以上独立样本	各组独立	检验各组中位数是否存在差异
Jonckheere	已知各组存在顺序关系	各组独立且有序	检验各组中位数是否存在趋势性差异

ANOVA的事后检验（post hoc test）

然后方差分析这里需要注意的一点是，我们的H1也就是备择假设只是说明组间有差异（至于是谁和谁有差异，其实不清楚），所以一般ANOVA之类的分析，在拒绝原假设之后，往往还需要做事后检验（post hoc test）。

Note that rejecting the null hypothesis does not indicate which of the groups differs. Post hoc comparisons between groups are required to determine which groups are different.

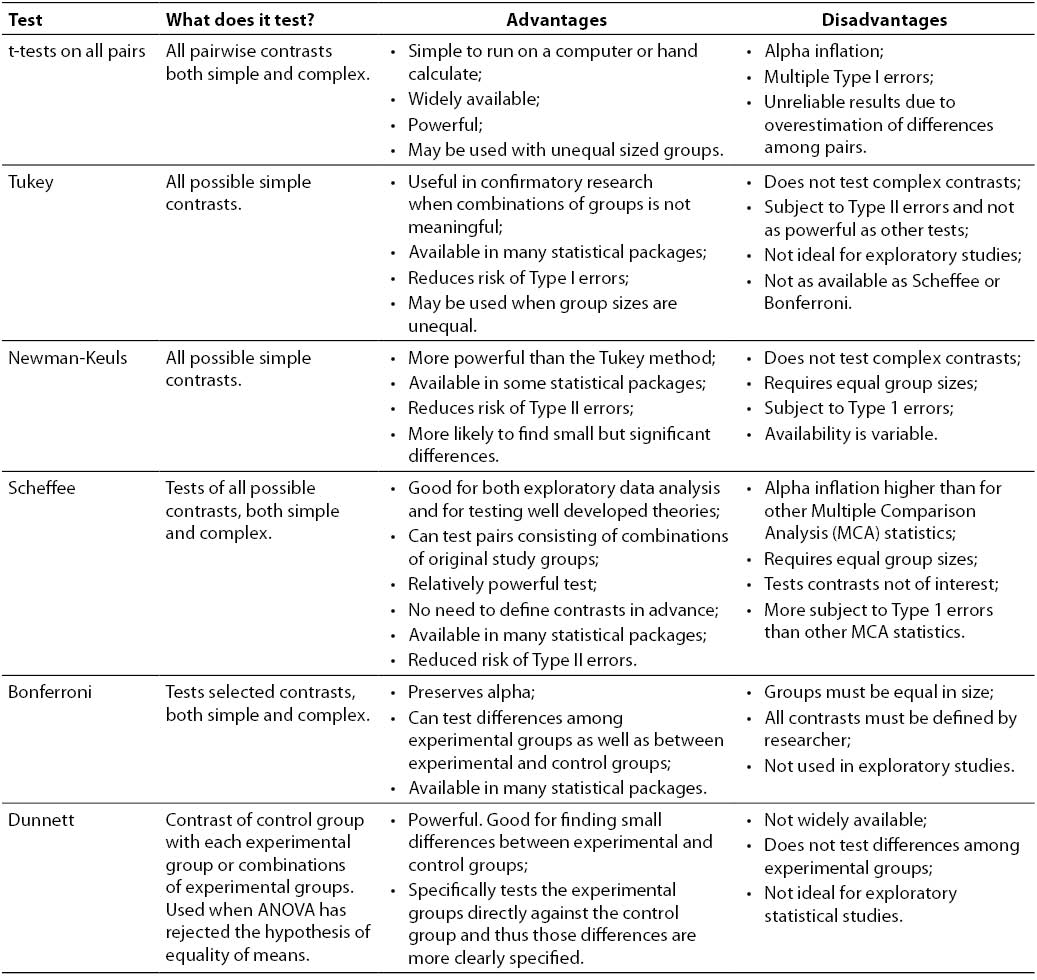
简单来说，ANOVA的事后检验（Post hoc tests）用于在总体F检验显著后，进一步探究是哪些组别之间存在显著的均值差异。事后检验可以控制多重比较导致的“第一类错误”上升的风险，常见的有Tukey、Bonferroni、Duncan和Scheffé等方法，它们根据不同的侧重点和适用场景来比较组间差异。

此处参考：https://pubmed.ncbi.nlm.nih.gov/22420233/

5. 相关性检验

检验场景	方法名称	定义与目的	前提条件	原假设 (H₀) vs. 备择假设 (H₁)	检验统计量
参数版本	皮尔逊相关系数检验 (scipy.stats.pearsonr)	评估两个连续变量之间的线性相关程度和显著性。	1. 两个变量均为连续数据。 2. 数据二元正态分布。 3. 关系是线性的。	H₀: 总体相关系数 ρ = 0（无线性相关） H₁: ρ ≠ 0 (存在线性相关)	皮尔逊相关系数 r
非参数版本	斯皮尔曼秩相关检验 (scipy.stats.spearmanr)	评估两个变量之间的单调相关程度和显著性。	1. 两个变量为连续或顺序数据。 2. 无需数据服从正态分布。 3. 关系是单调的（不一定线性）。	H₀: 总体等级相关系数 ρ_s = 0（无单调相关） H₁: ρ_s ≠ 0 (存在单调相关)	斯皮尔曼等级相关系数 ρ_s： 对数据单独排序后，计算其秩次之间的皮尔逊相关系数。

---

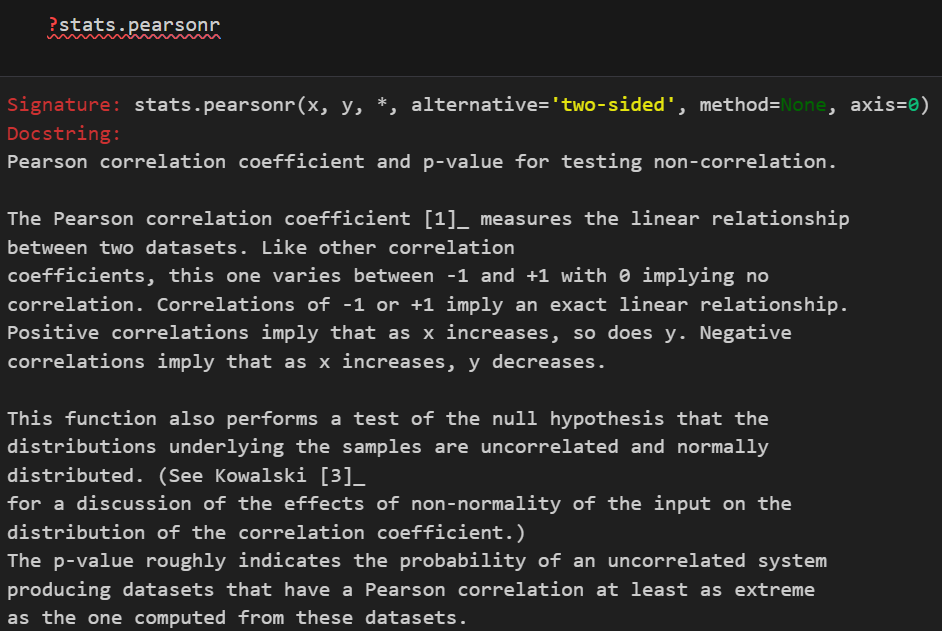
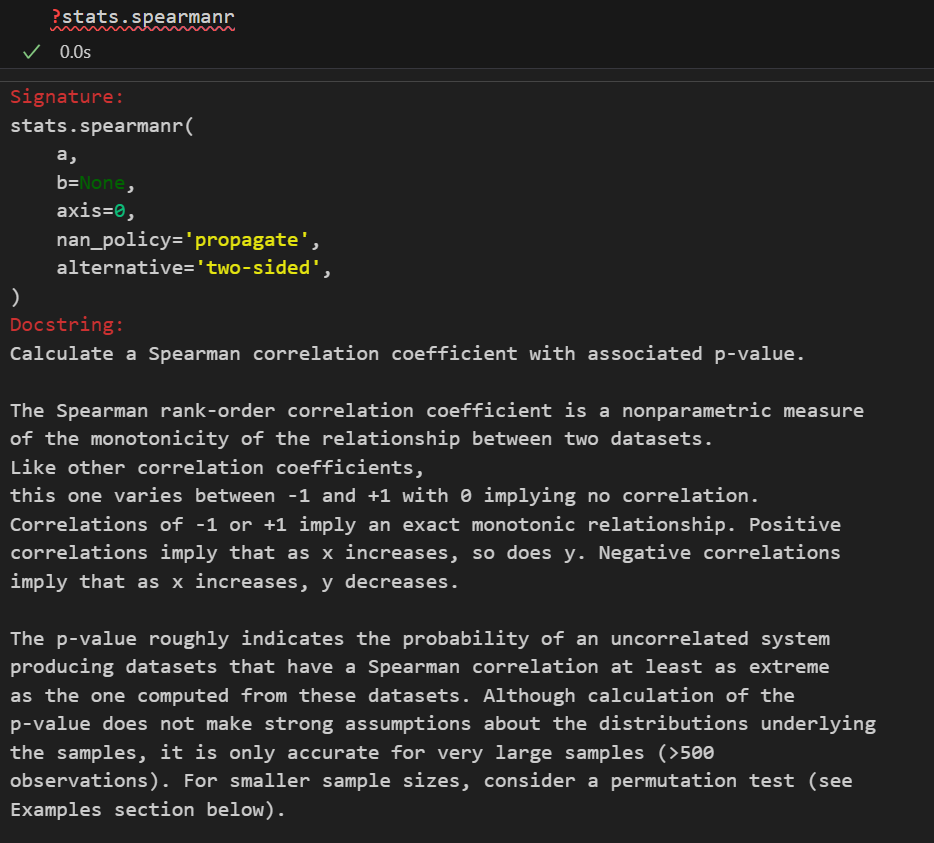
题外话：如果要是做相关性分析的话，Pandas 提供了 DataFrame.corr()，注意3个method

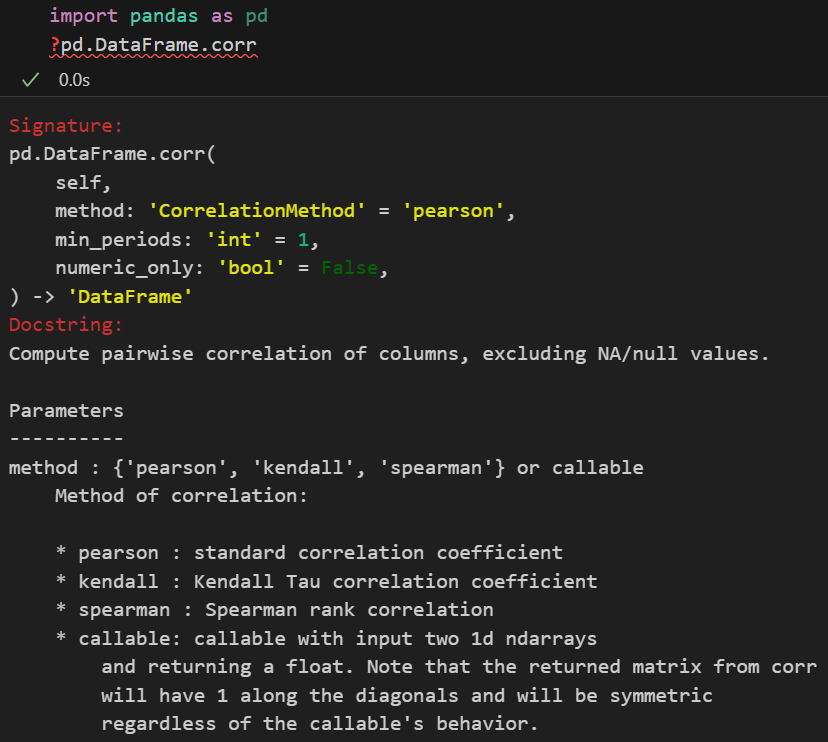
下面就是补充前面提到的3条件：独立、正态总体、方差齐性 3条件的检验方面

6. 正态性检验

检验场景	方法名称	定义与目的	前提条件	原假设 (H₀) vs. 备择假设 (H₁)	检验统计量
常用版本	Shapiro-Wilk 检验 (scipy.stats.shapiro)	检验一个数据集是否偏离正态分布。	1. 数据连续。 2. 样本量通常建议在3到5000之间。	H₀: 样本来自正态分布的总体 H₁: 样本不是来自正态分布的总体	W 统计量： 通过数据与正态分数相关的回归系数计算。W值越接近1，越像正态。
强大版本	Anderson-Darling 检验 (scipy.stats.anderson)	检验一个数据集是否偏离指定分布（如正态分布），对尾部差异更敏感。	1. 数据连续。 2. 可针对多种分布进行检验。	H₀: 样本来自指定分布的总体 H₁: 样本不是来自指定分布的总体	A² 统计量： 基于经验分布函数与理论分布函数之差的加权平方。

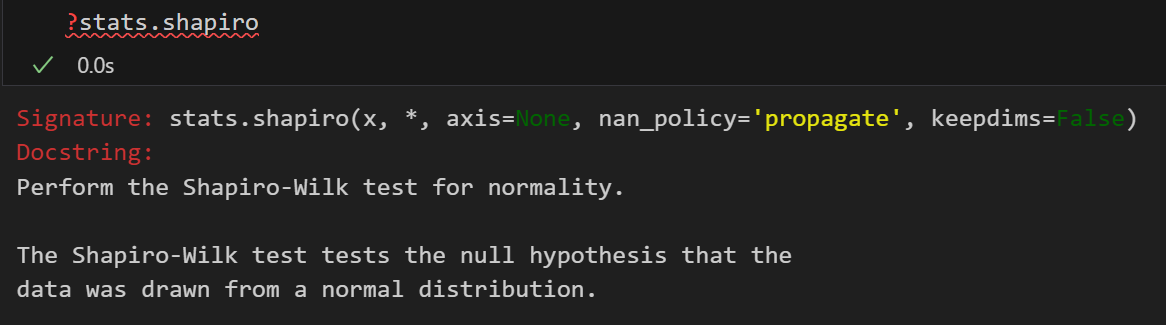
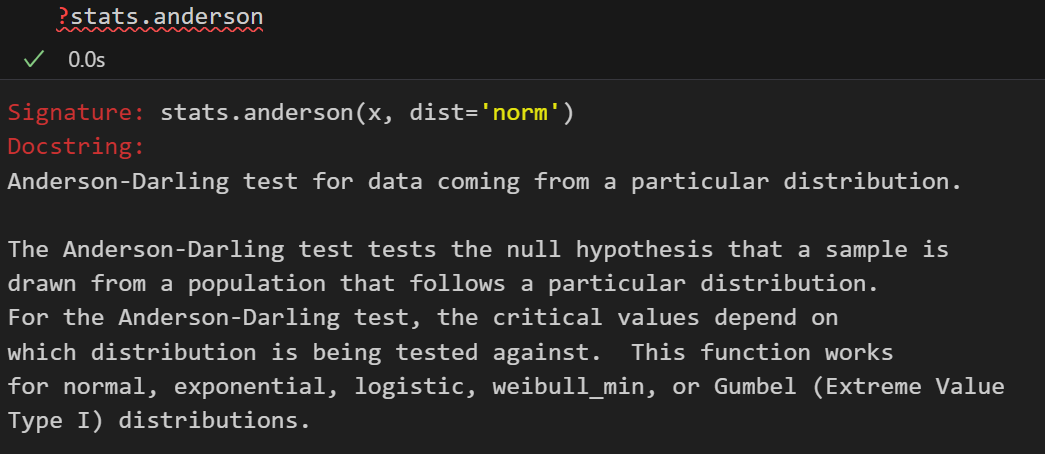
实际上检验方法有很多，

中文的，可以参阅下面这篇博客：
https://blog.csdn.net/qq_33924470/article/details/114668701

7. 方差齐性检验

方差齐性检验（Homogeneity of variance test）是用于检验不同样本总体方差是否相等的统计方法，其目的是在进行方差分析（ANOVA）或回归分析前，判断数据是否满足这些方法的假设前提条件，以避免分析结果产生偏差。

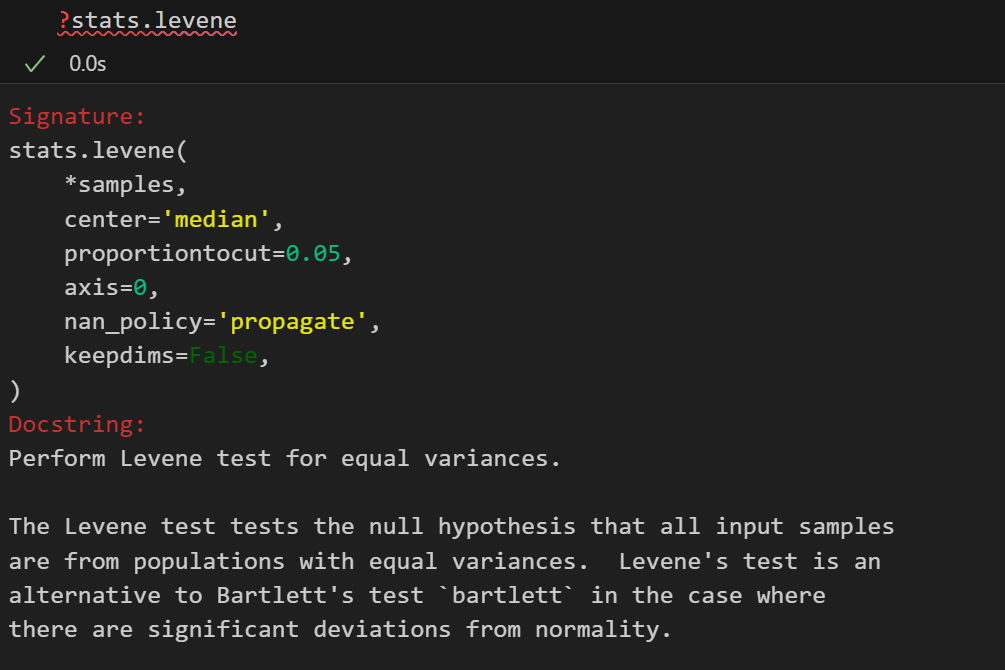
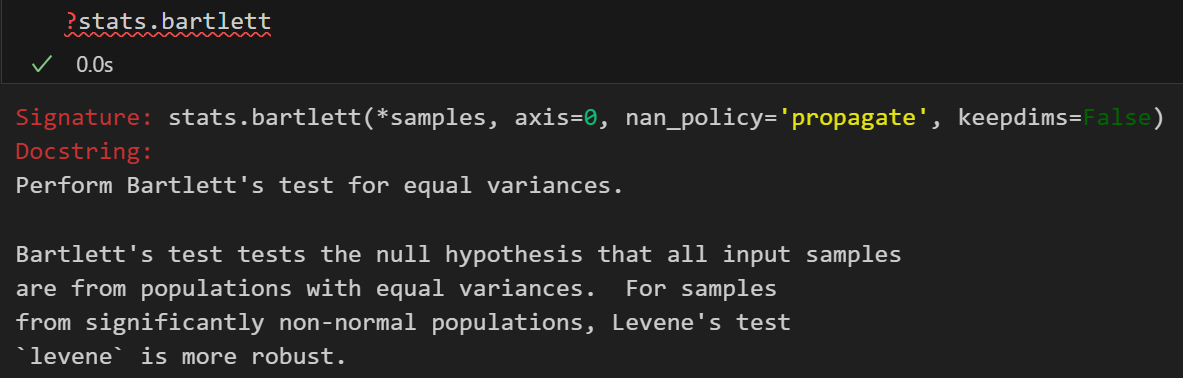
常用的方法包括Levene检验（适用于非正态数据）和Bartlett检验（适用于近似正态分布数据）。

更推荐使用Levene检验。

检验结果的p值若小于设定的显著性水平（通常为0.05），则拒绝原假设，认为方差不齐，此时应选择非参数检验或其他替代方法；反之，则接受方差齐的结论，可继续使用参数方法。

stats.bartlett
stats.levene

四，总结：知其然，更要知其所以然

会调API，但更重要的是知道在什么时候调用什么API（一系列试错与检验，再最终决定使用什么方法）

✅本来这篇博客很早就打算发出来了，包括后面的正态总体检验以及方差齐性检验，也都表格比对列了出来，但是数学公式都是用latex敲的，导出的时候markdown格式渲染不对，图片都是空白失效，一气之下删了点，结果丢了部分结果，其余的公式部分只能截图原稿。
有时间再整理补充部分。

参考：

https://pmc.ncbi.nlm.nih.gov/articles/PMC4754273/

https://pubmed.ncbi.nlm.nih.gov/22420233/

https://zh.wikipedia.org/zh-cn/%E5%81%87%E8%AA%AA%E6%AA%A2%E5%AE%9A

https://zh.wikipedia.org/wiki/%E7%84%A1%E6%AF%8D%E6%95%B8%E7%B5%B1%E8%A8%88