对于牛客网—语言学习篇—编程初学者入门训练—复合类型：BC140 杨辉三角、BC133 回型矩阵、BC134 蛇形矩阵题目的解析

开篇介绍：

hello 大家，前三篇博客已经将牛客网—语言学习篇—编程初学者入门训练—复合类型：二维数组中的大部分题目都讲完了，那么在本篇博客中，这一部分的练习也将迎来结束，在本文中，我将对剩下的BC140 杨辉三角、BC133 回型矩阵、BC134 蛇形矩阵这三道题目进行解析，值得一提的是，这三题的难度也并不是很大，关键就在于我们思维的突破以及推算、模拟能力，而这一些能力，也是我们学习、解决二维数组所不可或缺的能力，我在这边也希望大家能够通过我的这几篇关于二维数组练习解析的博客提高自己的编程能力。

接下来我便将这三道题目的链接给大家，希望大家可以在看解析之前就自己去尝试着作答题目，毕竟纸上得来终觉浅，绝知此事要躬行，愿大家不止于看，能够动手一字一符的敲出属于自己的代码。

杨辉三角_牛客题霸_牛客网https://www.nowcoder.com/practice/e671c6a913d448318a49be87850adbcc?tpId=290&tqId=618638&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290回型矩阵_牛客题霸_牛客网https://www.nowcoder.com/practice/36d5dfddc22c4f5b88a5b2a9de7db343?tpId=290&tqId=311134&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290蛇形矩阵_牛客题霸_牛客网https://www.nowcoder.com/practice/f228a074c5274619b26be544962375e1?tpId=290&tqId=311135&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290接下来，我们便开始讲解题目。

BC140 杨辉三角：
 

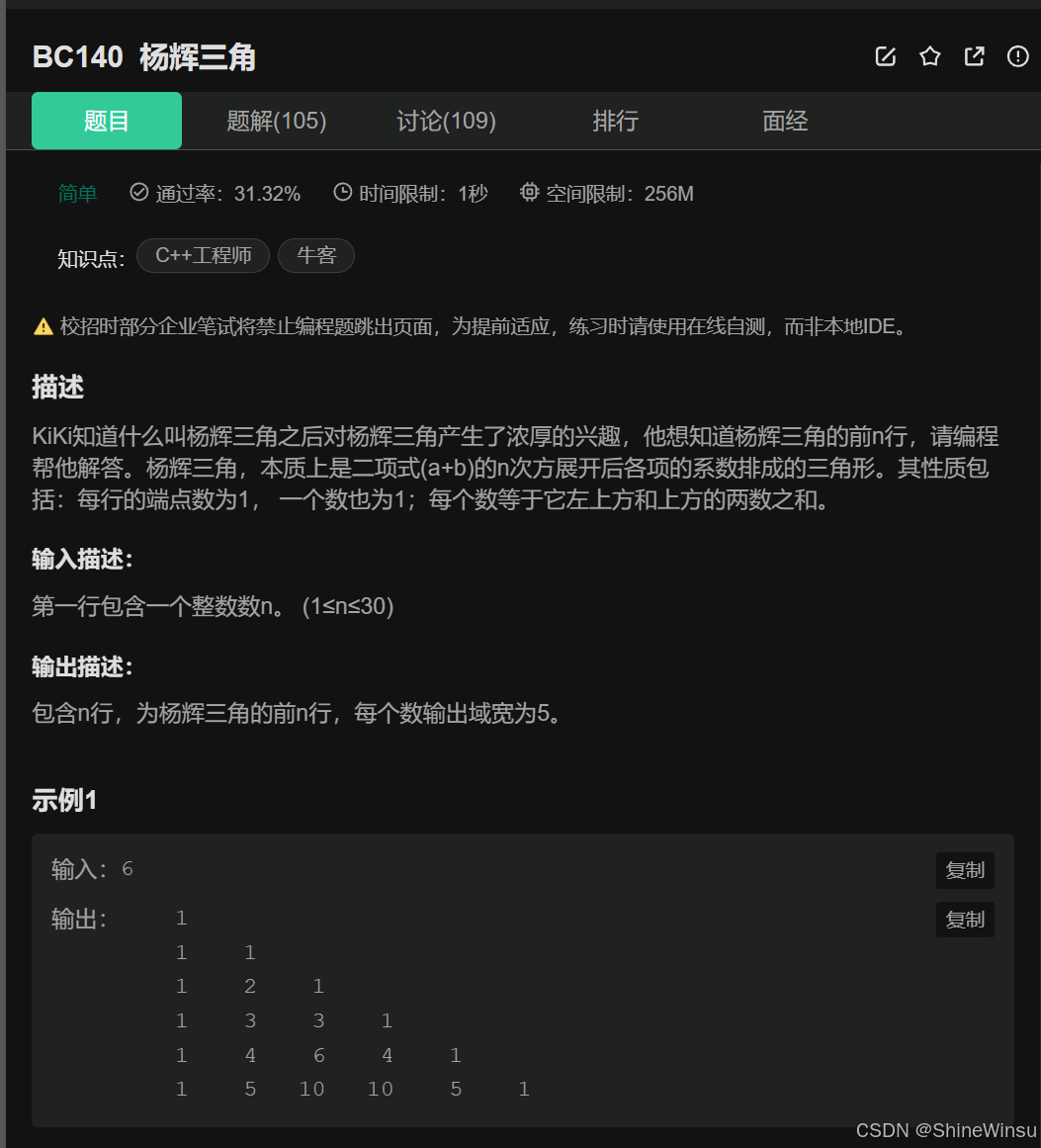
这道题，想必大家也肯定不会陌生，大名鼎鼎的杨辉三角，大家在初中的时候便应该又在数学课本后的趣味扩展见过它，那么在本题中，我们便要使用代码去实现杨辉三角，我们先看题目：

不过在分析题意之前，我先帮大家复习复习杨辉三角的概念及性质：

杨辉三角：

杨辉三角（又称帕斯卡三角）是数学中一种重要的离散型数阵，其核心是揭示二项式系数的分布规律，在组合数学、数论、代数等领域均有广泛应用。它最早由中国南宋数学家杨辉在 1261 年的《详解九章算法》中记载（提及 “贾宪用此术”，故又称 “贾宪三角”），而欧洲直到 17 世纪才由法国数学家帕斯卡系统研究，因此中国对其发现早于欧洲约 500 年。

一、杨辉三角的概念

杨辉三角是一个等腰三角形数阵，其构造规则简单但蕴含深刻规律，具体定义如下：

1. 边界元素：数阵的第 1 行只有 1 个元素，即1；从第 2 行开始，每行的首尾两个元素均为 1（无论行数多少，边界始终为 1）。
2. 内部元素：每行中除首尾外的任意一个元素，等于它上方相邻两个元素之和。

若用数学符号表示（设行数从第 0 行开始，每行的元素位置从第 0 列开始），则第n行第k列的元素（记为C(n,k)）满足：

• 当k=0或k=n时，C(n,k)=1（边界条件）；
• 当0<k<n时，C(n,k)=C(n-1,k-1)+C(n-1,k)（递推公式）。

杨辉三角的前 8 行（从第 0 行开始）示例：

plaintext

第0行：          1
第1行：        1   1
第2行：      1   2   1
第3行：    1   3   3   1
第4行：  1   4   6   4   1
第5行：1   5  10  10   5   1
第6行：1   6  15  20  15   6   1
第7行：1   7  21  35  35  21   7   1

二、杨辉三角的核心性质

杨辉三角的性质可从数阵结构、数值关系、数学应用三个维度展开，每一条性质都对应明确的数学意义：

1. 结构对称性

• 性质描述：杨辉三角的每一行都是 “对称” 的，即第n行第k列的元素与第n行第n-k列的元素相等，数学表达式为C(n,k)=C(n,n-k)。
• 本质原因：组合数的对称性 —— 从n个元素中选k个元素的组合数，与从n个元素中选n-k个元素（即排除k个元素）的组合数相等。
• 示例：第 5 行中，C(5,1)=5，C(5,4)=5；C(5,2)=10，C(5,3)=10，完全对称。

2. 行元素和的规律

• 性质描述：第n行所有元素的和等于2ⁿ（n从 0 开始）。
• 推导过程：
  1. 从组合数角度：第n行元素是C(n,0), C(n,1), ..., C(n,n)，根据二项式定理，(a+b)ⁿ = Σ（从k=0到n）C(n,k)aⁿ⁻ᵏbᵏ；
  2. 令a=b=1，则(1+1)ⁿ = ΣC(n,k) = 2ⁿ，即该行元素和为2ⁿ。
• 示例：第 3 行元素和为1+3+3+1=8=2³；第 4 行和为1+4+6+4+1=16=2⁴。

3. 列元素和的规律

• 性质描述：第k列（从 0 列开始）所有元素的和等于第k+1列的下一个元素，即C(0,k)+C(1,k)+C(2,k)+...+C(n,k)=C(n+1,k+1)（n≥k）。
• 本质原因：组合数的 “累加公式”（又称 “朱世杰恒等式” 的特殊形式），可通过数学归纳法或组合意义证明（如 “从n+1个元素中选k+1个，可按第 1 个元素是否选中分类，最终累加得到等式”）。
• 示例：第 2 列（元素为1,3,6,10,...）中，C(2,2)+C(3,2)+C(4,2)=1+3+6=10=C(5,3)，与第 3 列第 5 行的元素一致。

4. 斜向元素和的规律

杨辉三角的 “斜行”（从左上到右下的斜线）元素和对应斐波那契数列，这是其最具趣味性的性质之一：

• 斜行定义：第 1 条斜线（最左侧）：1,1,1,1,...；第 2 条斜线：1,2,3,4,...；第 3 条斜线：1,3,6,10,...；第 4 条斜线：1,4,10,20,...。
• 性质描述：从第 3 条斜线开始，任意一条斜线中前m个元素的和，等于下一条斜线的第m个元素；且相邻两条斜线的元素对应相加，得到下一条斜线的元素，最终形成斐波那契数列（1,1,2,3,5,8,...）。
• 示例：
  • 第 2 条斜线前 3 个元素：1+2+3=6，等于第 3 条斜线第 3 个元素（6）；
  • 斐波那契数列推导：第 1 条斜线元素（1,1,1,1）+ 第 2 条斜线元素（1,2,3）= 第 3 条斜线元素（2,3,4），最终提取关键和为1,1,2,3,5,8,...。

5. 与素数的关系

• 性质描述：若第p行（p为素数）的行数p是素数，则该行中除首尾的两个1外，其余所有元素都能被p整除（即元素均为p的倍数）。
• 本质原因：素数的整除性 —— 当p为素数且0<k<p时，组合数C(p,k)=p!/(k!(p-k)!)，分子中p是素数，而分母k!(p-k)!的所有因子均小于p（无法整除p），因此C(p,k)必含因子p，即能被p整除。
• 示例：第 5 行（p=5，素数）元素为1,5,10,10,5,1，中间元素5,10,10,5均能被 5 整除；第 7 行（p=7）中间元素7,21,35,35,21,7均能被 7 整除。

6. 与二项式系数的直接对应

这是杨辉三角的核心数学意义：

• 对于任意正整数n，二项式(a+b)ⁿ展开式的系数，恰好是杨辉三角第n行的所有元素。
• 示例：
  • (a+b)¹ = 1a + 1b，系数对应第 1 行（1,1）；
  • (a+b)² = 1a² + 2ab + 1b²，系数对应第 2 行（1,2,1）；
  • (a+b)³ = 1a³ + 3a²b + 3ab² + 1b³，系数对应第 3 行（1,3,3,1）。

题意分析：

知道了杨辉三角的概念以及性质之后，我们便来看看题目想要我们做什么：

这道题是要求我们编程输出杨辉三角的前 n 行。

输入输出分析

• 输入：一个整数 n（1≤n≤30），表示要输出杨辉三角的前 n 行。
• 输出：杨辉三角的前 n 行，每个数的输出域宽为 5。

杨辉三角的生成规则

• 每行的第一个和最后一个数都是 1。
• 对于每行中间的数，每个数等于它上方相邻两个数之和。

解题思路：

首先跟据上面的题意分析，我们可以知道，我们要用类二维数组的方式去表达出杨辉三角的每一个值，但是我们要使用二维数组吗？其实是不用的，我们只是要表达值，而在二维数组中我们并没有办法直接计算值，所以我们只能用双重循环，去找到杨辉三角的每个元素的坐标，去看看有没有蛛丝马迹让我们有迹可循，所以，我们先来看看题目所给示例的每个元素的坐标：

我们可以将杨辉三角的行从上到下编号为第 0 行、第 1 行、第 2 行……，每行的元素从左到右编号为第 0 列、第 1 列、第 2 列……。以下是每个元素的坐标（行，列）：

• 第 0 行：(0,0)
• 第 1 行：(1,0)，(1,1)
• 第 2 行：(2,0)，(2,1)，(2,2)
• 第 3 行：(3,0)，(3,1)，(3,2)，(3,3)
• 第 4 行：(4,0)，(4,1)，(4,2)，(4,3)，(4,4)
• 第 5 行：(5,0)，(5,1)，(5,2)，(5,3)，(5,4)，(5,5)

我们知道，杨辉三角中的两侧都得是1，所以，我们可以先从两侧的1入手，根据上面的坐标，我们不难发现，第一列都是1，也就是说我们要让j==0时，都表达1，如此一来，就解决了左侧的1的表达，那么每一行的最后一个1，我们要怎么表达呢？

对于最右侧1的表达的问题：

这时候大家可能会说，每一行的最后一个1的行坐标都对于列坐标，那我们可以设置判断条件：当i==j的时候，就表达1，那么，这个方法能行吗？答案是：可以的，但是又不可以，关键在于我们要如何实现了，在这里我先直接透露代码，大家可以在看完了后面的分析之后，再看这一段

假如我们使用这一段代码，那么就不能：

#include <stdio.h>
int main()
{int n = 0;int coef = 1;scanf("%d",&n);for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){if (i == 0 || j == 0){coef = 1;}else{coef = coef * (i - j + 1) / j;}printf("%5d",coef);}printf("\n");}return 0;
}

原因：

问题分析

在代码中，coef 是一个全局的（在 main 函数内全局使用）变量，用于递推计算杨辉三角当前位置的系数。但代码的逻辑是：

• 当 i == 0（第 0 行）或者 j == 0（每行第 0 列）时，将 coef 设为 1。
• 其他情况下，用 coef = coef * (i - j + 1) / j 递推计算当前系数。

然而，coef 在每行的计算中没有正确重置。例如，在计算第 i 行第 j 列的系数时，coef 保留了第 i 行第 j-1 列计算后的结果，这本身是对的（因为杨辉三角每个内部元素是上方两元素之和，递推计算符合这个逻辑）。但当开始计算下一行（i 增加）时，coef 并没有被正确初始化为下一行第 0 列的初始值 1（除了 i == 0 或者 j == 0 时会设置，但下一行的 j 循环是从 0 开始，j == 0 时会设置 coef = 1，这部分看似对，但结合递推逻辑，整体还是有问题）。

更关键的是，递推公式 coef = coef * (i - j + 1) / j 依赖于上一个位置（同一行前一列）的 coef 值，而如果在每行的第 0 列（j == 0）时将 coef 设为 1，然后计算第 1 列时，用 coef = 1 * (i - 0 + 1) / 1 = i + 1，这在第 1 行（i = 1）时是对的（第 1 行第 1 列应该是 1，此时 i + 1 = 2，错误）。这说明递推公式的应用场景和初始化逻辑不匹配。

正确逻辑

杨辉三角的正确生成应该是：

• 每行的第 0 列和第 i 列（每行最后一列）的系数为 1。
• 所以我们才要

  if (i == 0 || j == 0)
  {coef = 1;
  }

  这样的重置每一行的coef，不难仅仅只是i==0是只能重置第一行的，无法重置每一行的第一个（也就是第一列），这么一来，就导致我们的coef无法正常递推

• 对于每行中间的列（0 < j < i），系数为上一行第 j - 1 列和第 j 列系数之和。

如果用递推公式（基于组合数公式 C(n,k)=C(n,k−1)×kn−k+1​），那么在每行的计算中，coef 应该从第 0 列的 1 开始，依次递推计算后面的列。但要注意，每行的 coef 递推应该是独立的，即每行开始时，coef 应该初始化为 1（第 0 列的系数），然后依次计算后面的列。

而如果我们想要使用i==j时元素要为0，我们就得在每次进入行i循环时就把coef进行重置为1，即如下：

#include <stdio.h>int main()
{int n = 0;scanf("%d", &n);for (int i = 0; i < n; i++){int coef = 1; // 每行开始时，coef初始化为1（第0列的系数）for (int j = 0; j <= i; j++){printf("%5d", coef);// 递推计算下一列的系数if (j < i)//当i==j的时候，不进入递推，即coef为1{coef = coef * (i - j) / (j + 1);}}printf("\n");}return 0;
}

即如上。

继续解题：

经过上文的分析，大家应该知道了，其实实现杨辉三角的关键就在于，递推公式的实现，我们要找到杨辉三角中行、列与所表达的元素的关系，那么具体是什么关系呢？大家先别急，我们先来思考一个问题。

我们知道说，想要表达出杨辉三角，要借助双重循环，那么，我们要怎么设置循环呢，首先关于行i的循环，大家应该很容易想到，毕竟题目中说了输入一个值n，表示要输出n行的杨辉三角，那么对于i，其实就是for(int i=0;i<n;i++)，这一步不难，可是对于列j循环，我们要怎么办呢？依然是看图：

对于i，它还有限制条件n可以用，但是对于j，我们要对其使用什么限制条件呢？首先可以明确，j要从0开始，毕竟还是需要第0列（1）列的，只是限制条件，它会是什么呢？它和n可没有关系，那么，我们可以看看它和i有什么关系呀，既然它明面上没有对象，但是我们可以去千里一线牵，去帮助它看看，它潜在的对象，如果大家能想到去寻找j和i的关系的话，那么恭喜大家，要成功了，我们不妨看看，i和j到底是什么关系呢？，我们可以看到，第0行，是有1个元素，而在第1行，是有2个元素，往下第n行，也是同样有n+1个元素，那么就得到规律了：

在杨辉三角里，第 i 行有 i+1 个元素，所以列索引 j 的取值范围是 0≤j≤i。也就是说，对于每一行 i，列 j 从 0 开始，到 i 结束，这样就能保证每行生成正确数量的元素，从而构建出完整的杨辉三角。

于是，我们便能得到两个循环了：

for (int i = 0; i < n; i++)
{for (int j = 0; j <= i; j++){}
}

即如上，这边再详细一下，由于我们是从0开始表达数据，所以如上，如果是从1开始，就会不一样了，大家可以自行探索一下。

知道了两个循环之后，我们便只剩下递推公式需要知道了，那么接下来，就为大家揭晓：

杨辉三角递推公式：

我们可以从组合意义的具体场景、递推过程的分步演示、特殊值验证三个角度，进一步拆解杨辉三角递推公式的细节，让其逻辑更清晰。

一、组合意义的具体场景：用 “选物品” 理解递推

递推公式 C(i,j)=C(i−1,j−1)+C(i−1,j) 的本质是组合数的分类计数原理，我们用一个具体场景解释：

假设一个袋子里有 i 个不同的球（编号为 1,2,...,i），现在要从中选 j 个球，总共有多少种选法？
根据组合数定义，答案是 C(i,j)。

我们可以按 “是否选第 i 个球” 分成两类情况：

1. 选第 i 个球：
   已经确定选第 i 个球，还需要从剩下的 i−1 个球（编号 1,2,...,i−1）中选 j−1 个，选法有 C(i−1,j−1) 种。

2. 不选第 i 个球：
   需要从全部 i−1 个球（编号 1,2,...,i−1）中选 j 个，选法有 C(i−1,j) 种。

根据 “分类计数时总方法数 = 各类方法数之和”，两类情况的和就是总选法数，即：C(i,j)=C(i−1,j−1)+C(i−1,j)。

这个场景完美对应了递推公式的逻辑 —— 杨辉三角的每个内部元素，都是 “包含上方左元素” 和 “包含上方右元素” 两种情况的总和。

二、递推过程的分步演示：从第 0 行生成第 5 行

我们从杨辉三角的第 0 行开始，逐行用递推公式生成元素，直观展示公式的应用过程：

1. 第 0 行（i=0）：
   只有 1 个元素，列索引 j=0，根据边界条件 C(0,0)=1，所以第 0 行为：[1]。

2. 第 1 行（i=1）：

   • 列 j=0：边界条件 C(1,0)=1
   • 列 j=1：边界条件 C(1,1)=1
     第 1 行为：[1, 1]（无内部元素，无需用递推公式）。

3. 第 2 行（i=2）：

   • 列 j=0：边界条件 C(2,0)=1
   • 列 j=1：内部元素，用公式 C(2,1)=C(1,0)+C(1,1)=1+1=2
   • 列 j=2：边界条件 C(2,2)=1
     第 2 行为：[1, 2, 1]。

4. 第 3 行（i=3）：

   • 列 j=0：C(3,0)=1
   • 列 j=1：C(3,1)=C(2,0)+C(2,1)=1+2=3
   • 列 j=2：C(3,2)=C(2,1)+C(2,2)=2+1=3
   • 列 j=3：C(3,3)=1
     第 3 行为：[1, 3, 3, 1]。

5. 第 4 行（i=4）：

   • 列 j=1：C(4,1)=C(3,0)+C(3,1)=1+3=4
   • 列 j=2：C(4,2)=C(3,1)+C(3,2)=3+3=6
   • 列 j=3：C(4,3)=C(3,2)+C(3,3)=3+1=4
     第 4 行为：[1, 4, 6, 4, 1]（首尾边界元素省略计算过程）。

通过分步计算可见：每一行的内部元素，都是上一行相邻两个元素 “叠加” 的结果，递推公式是生成整个三角的 “引擎”。

三、特殊值验证：公式的普适性

为了确认递推公式的正确性，我们用几个特殊值验证：

1. 当 j=1 时：
   公式简化为 C(i,1)=C(i−1,0)+C(i−1,1)。

   • 已知 C(i−1,0)=1，而 C(i−1,1)=i−1（从 i−1 个元素中选 1 个，有 i−1 种选法）。
   • 因此 C(i,1)=1+(i−1)=i，这与实际一致（第 i 行第 1 列的元素确实是 i，如第 4 行第 1 列是 4，第 5 行第 1 列是 5）。

2. 当 j=i-1 时：
   由对称性 C(i,i−1)=C(i,1)=i，用公式验证：C(i,i−1)=C(i−1,i−2)+C(i−1,i−1)=(i−1)+1=i，与实际一致。

3. 当 i=5, j=2 时：
   第 5 行第 2 列的元素应为 10，用公式计算：C(5,2)=C(4,1)+C(4,2)=4+6=10，正确。

四、递推公式的 “反向验证”：从元素反推来源

杨辉三角的每个内部元素都能找到它的 “父元素”，例如：

• 第 5 行第 2 列的 10，来自第 4 行第 1 列的 4 和第 4 行第 2 列的 6（4+6=10）。
• 第 6 行第 3 列的 20，来自第 5 行第 2 列的 10 和第 5 行第 3 列的 10（10+10=20）。

这种 “可追溯性” 进一步证明了递推公式的正确性 —— 整个杨辉三角的所有元素，都是从第 0 行的 1 开始，通过无数次 “两数相加” 的递推生成的。

总结来说，杨辉三角的递推公式 C(i,j)=C(i−1,j−1)+C(i−1,j) 不是凭空定义的，它是组合计数逻辑的必然结果，也是杨辉三角 “自下而上” 构造的核心规则。无论是数学证明、实际场景还是分步计算，都能验证这一公式的合理性。

所以，用于编程中，递推公式就变成了coef = coef * (i - j + 1) / j

coef = coef * (i - j + 1) / j 这个公式是基于组合数的递推关系，用于在不存储整个杨辉三角的情况下，从左到右计算每行的元素值。我们可以从数学原理和实际计算过程两方面详细解释：

一、公式的数学来源

杨辉三角的第 i 行第 j 列元素对应组合数 C(i,j)（从 i 个元素中选 j 个的方案数）。组合数有一个重要的递推关系：
C(i,j)=C(i,j−1)×ji−j+1​
这个公式的推导过程如下：

1. 根据组合数定义：
   C(i,j)=j!⋅(i−j)!i!​,C(i,j−1)=(j−1)!⋅(i−j+1)!i!​
2. 两式相除得：
   C(i,j−1)C(i,j)​=j!⋅(i−j)!(j−1)!⋅(i−j+1)!​=ji−j+1​
3. 整理后得到：
   C(i,j)=C(i,j−1)×ji−j+1​

这就是代码中 coef = coef * (i - j + 1) / j 的数学依据 ——coef 本质上是在迭代计算组合数 C(i,j)。

二、代码中的实际作用

在代码中，coef 变量的作用是 “滚动计算” 当前行的元素：

• 每行开始时，coef 被初始化为 1，对应 C(i,0)=1（每行第一个元素）。
• 随后通过上述公式，从左到右依次计算第 j=1,2,...,i 个元素，每次计算都基于上一个元素（j-1 列）的结果。

三、分步计算示例（以第 4 行为例）

第 4 行（i=4）的元素应为 1, 4, 6, 4, 1，我们用公式模拟计算过程：

1. 初始值：j=0 时，coef = 1（对应 C(4,0)=1）。
2. 计算 j=1：
   coef=1×14−1+1​=1×4/1=4（对应 C(4,1)=4）
3. 计算 j=2：
   coef=4×24−2+1​=4×3/2=6（对应 C(4,2)=6）
4. 计算 j=3：
   coef=6×34−3+1​=6×2/3=4（对应 C(4,3)=4）
5. 计算 j=4：
   coef=4×44−4+1​=4×1/4=1（对应 C(4,4)=1）

可见，通过公式从左到右迭代，恰好能生成整行的元素，且无需存储上一行的数据，极大节省了空间。

四、关键注意点

1. 整数除法的有效性：公式中虽然有除法，但由于组合数一定是整数，coef * (i-j+1) 一定能被 j 整除（例如第 4 行 j=2 时，4×3=12 能被 2 整除），因此不会出现小数或精度损失。
2. 迭代顺序：必须从左到右计算（j 从 1 到 i），因为每个元素的计算依赖于左侧相邻元素的结果。
3. 空间效率：这种方式无需数组，仅用一个变量 coef 即可完成计算，空间复杂度为 O(1)。

这个公式的巧妙之处在于，它将 “依赖上一行元素” 的递推关系，转化为 “依赖同一行左侧元素” 的递推，从而实现了无数组的高效计算。

完整代码：

到了这里，大家应该就已经洞悉杨辉三角如何在不使用数组的情况下，使用双重循环以及递推公式进行表达了，下面我们便给出完整代码：

#include <stdio.h>int main()
{int n = 0;int coef = 1;scanf("%d",&n);for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){if (i == 0 || j == 0){coef = 1;}else{coef = coef * (i - j + 1) / j;}printf("%5d",coef);}printf("\n");}return 0;
}

如果大家想要使用i==j的时候，coef也为1，则是如下代码：

#include <stdio.h>int main() {int n;printf("请输入杨辉三角的行数: ");scanf("%d", &n);for (int i = 0; i < n; i++) {// 计算并打印当前行的每个元素int coef = 1;  // 每行第一个元素都是1printf("%5d", coef);for (int j = 1; j <= i; j++) {// 利用组合数递推公式计算下一个元素// C(i,j) = C(i,j-1) * (i-j+1)/jcoef = coef * (i - j + 1) / j;printf("%5d", coef);其作用是让每个数字占据固定宽度并对齐，确保三角结构整齐}printf("\n");}return 0;
}

这边给大家讲一下为什么表达coef时要用%5d：

在杨辉三角代码中，printf("%5d", coef); 是控制元素输出格式的核心语句，其作用是让每个数字占据固定宽度并对齐，确保三角结构整齐。以下是逐部分的详细注释和逻辑拆解：

1. 语句整体功能

// 按照 "占5个字符宽度的十进制整数" 格式，输出当前杨辉三角元素 coef 的值
// 核心作用：统一每个数字的显示宽度，避免因数字位数不同导致三角结构错乱
printf("%5d", coef);

 

2. 格式控制符 %5d 逐字符解析

%5d 是 printf 的格式说明符，专门用于控制十进制整数的输出格式，各部分含义如下：=

格式字符	作用解释
%	格式说明符的起始标记，告诉 printf 后续字符是格式控制指令（而非普通字符串）
5	宽度指定符：表示当前输出的整数需要占据 5 个字符的固定宽度
d	类型转换符：表示输出的数据是 int 类型（十进制整数）

3. 关键特性：右对齐与空格填充

当数字本身的位数 小于 5 时，printf 会在数字左侧自动补空格，保证总宽度为 5；若数字位数 等于或大于 5（如较大的组合数），则会突破 5 个字符宽度，优先保证数字完整显示（避免截断）。

示例（以 coef 为不同值时的输出效果）：

coef 的值	实际输出内容（方框代表空格，共 5 个字符位置）	说明
1	□□□□1（4 个空格 + 数字 1）	1 是 1 位数，左侧补 4 个空格
6	□□□□6（4 个空格 + 数字 6）	同上，统一左补空格
10	□□□10（3 个空格 + 数字 10）	10 是 2 位数，左侧补 3 个空格
21	□□□21（3 个空格 + 数字 21）	同上，按位数补对应空格
120	□□120（2 个空格 + 数字 120）	120 是 3 位数，左侧补 2 个空格

4. 在杨辉三角中的核心作用

杨辉三角的元素随行数增加，数字位数会逐渐变多（如第 10 行有两位数，第 20 行有三位数）。若不控制宽度，输出会混乱（例如 “1” 和 “10” 并排时，前者占 1 位、后者占 2 位，导致下一行元素无法对齐）。

反例（无宽度控制的混乱效果）：

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1  // 这里“10”占2位，导致后续行对齐错位
1 6 15 20 15 6 1  // 错位会越来越明显

正例（%5d 控制后的整齐效果）：

    1  // 1占1位，左补4个空格（共5位）1    1  // 每个1都左补4个空格1    2    1  // 2左补4个空格，与1对齐1    3    3    11    4    6    4    11    5   10   10    5    1  // 10左补3个空格，仍占5位，与其他元素对齐1    6   15   20   15    6    1  // 所有元素均占5位，三角结构整齐

5. 灵活调整：宽度与对齐方式的修改

若需要调整显示效果，可修改 %5d 中的 “5” 或添加对齐标志：

• 增大宽度：如 %6d，表示每个数字占 6 个字符宽度（适合更大的杨辉三角，避免数字重叠）。
• 左对齐：如 %-5d，在宽度前加 “-”，表示数字靠左显示，右侧补空格（默认是右对齐，左侧补空格）。
  • 示例：coef=10 用 %-5d 输出为 10□□□（10 靠左，右侧补 3 个空格）。

总结

printf("%5d", coef); 的核心价值是通过固定宽度实现元素对齐，是杨辉三角从 “混乱数字序列” 变成 “整齐等腰三角” 的关键。其本质是利用格式控制符，为每个数字分配统一的 “显示位置”，无论数字位数多少，都能保证三角结构的对称性和可读性。

不过呢，大家平时熟悉的杨辉三角，应该是这个样子的：

即每行前面是有空格的，这样子才算是三角形，那么这中的杨辉三角，要怎么实现呢？其实不难，只需要用到前导空格打印即可，关于这方面的知识，大家可以看这篇博客：对于牛客网—语言学习篇—编程初学者入门训练—循环输出图形的一些总结-CSDN博客

里面便讲述了如何实现前导空格打印，我们这边就直接给出完整代码：

#include <stdio.h>int main() {int n;printf("请输入杨辉三角的行数: ");scanf("%d", &n);for (int i = 0; i < n; i++) {// 打印前导空格，使三角形居中对齐// 每行的空格数 = (总行数 - 当前行 - 1) for (int k = 0; k < (n - i - 1) ; k++) {printf("  ");//两个空格哦}int coef = 1;  // 每行第一个元素为1for (int j = 0; j <= i; j++) {printf("%4d", coef);  // 每个数字占4个字符宽度// 计算下一个系数if (j < i) {coef = coef * (i - j) / (j + 1);}}printf("\n");  // 每行结束后换行}return 0;
}

到此，杨辉三角大功告成。

BC133 回型矩阵：

这道题，其实不难，大家不要被唬到，我们先看题目：

题意分析：

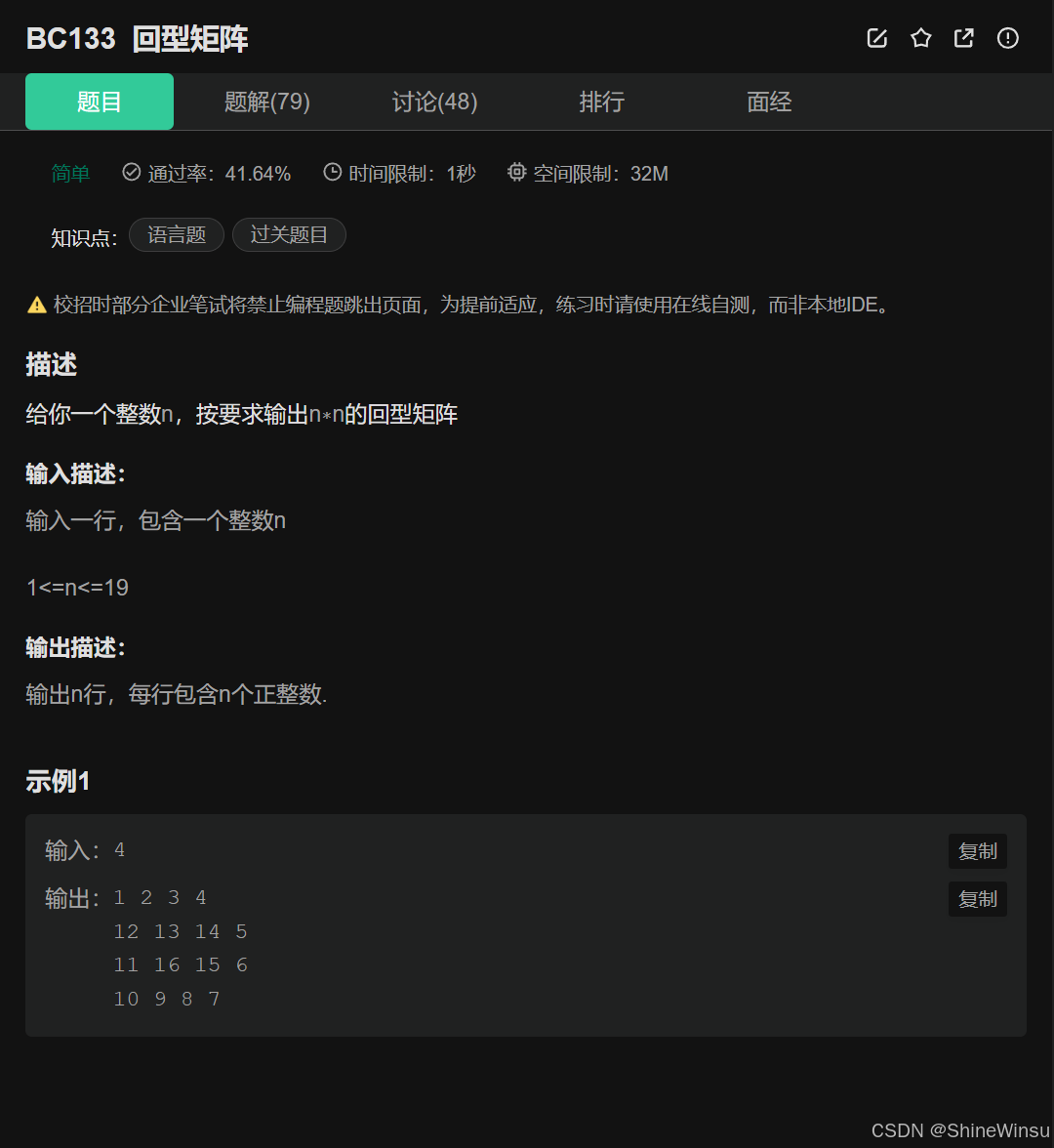
这道题是要求我们根据输入的整数 n，生成一个 n×n 的回型矩阵。

输入输出分析

• 输入：一个整数 n（1≤n≤19），表示要生成的回型矩阵的行数和列数。
• 输出：n 行，每行包含 n 个正整数，这些正整数按回型（螺旋）的方式排列。

回型矩阵的生成规则

回型矩阵的元素是按照螺旋的顺序依次填充的。以示例输入 4 为例，输出的矩阵元素是从 1 开始，先按行从左到右填充第一行，然后按列从上到下填充最后一列，接着按行从右到左填充最后一行，再按列从下到上填充第一列，以此类推，直到填充完整个矩阵。

继续解答：

大家一定要详细理解回型矩阵的生成规则，它将是我们解答本题的重中之重，为了加深大家理解，我们标出每个元素的坐标：

元素	坐标（行，列）
1	(0, 0)
2	(0, 1)
3	(0, 2)
4	(0, 3)
12	(1, 0)
13	(1, 1)
14	(1, 2)
5	(1, 3)
11	(2, 0)
16	(2, 1)
15	(2, 2)
6	(2, 3)
10	(3, 0)
9	(3, 1)
8	(3, 2)
7	(3, 3)

光看这个可能不太明显，我们看按照大小顺序的元素各自坐标：

元素	坐标（行，列）
1	(0, 0)
2	(0, 1)
3	(0, 2)
4	(0, 3)
5	(1, 3)
6	(2, 3)
7	(3, 3)
8	(3, 2)
9	(3, 1)
10	(3, 0)
11	(2, 0)
12	(1, 0)
13	(1, 1)
14	(1, 2)
15	(2, 2)
16	(2, 1)

这样子，大家应该就能看得明白多了，实际上就是从小到大，先填充第一行，然后填充最后一列，再填充最后一行，接着填充第一列，数字大小还没到n*n时，就继续填充第二列，然后倒二列，再然后倒二行，如此循环往复下去。

那么，这就需要我们对循环的限制条件以及开始，有着极高的要求，我们要让填充完第一行后，就能到最后一列（即移动到第二行的最后一列），且保持列坐标不动，行坐标++(注意不要越界访问)，下面是具体实现所需的步骤：

要生成 n×n 的回型矩阵（螺旋排列的矩阵），核心思路是从外到内分层填充，通过控制 “上、下、左、右” 四个边界的收缩，逐步完成所有元素的排列，具体步骤如下：

一、准备工作：明确基础信息

1. 确定矩阵范围：矩阵共 n 行、n 列，需要填充从 1 到 n2 的所有整数（每个数仅用一次）。
2. 定义四个边界：
   • 上边界：初始为第 0 行（矩阵最上方的行）；
   • 下边界：初始为第 n−1 行（矩阵最下方的行）；
   • 左边界：初始为第 0 列（矩阵最左侧的列）；
   • 右边界：初始为第 n−1 列（矩阵最右侧的列）；
3. 初始化填充数字：从数字 1 开始填充。

二、核心步骤：螺旋填充（从外到内）

循环执行以下 4 个方向的填充，直到所有数字（1 到 n2）都被填充完毕：

1. 第一步：填充 “上边界”（从左到右）

• 目标区域：当前 “上边界” 所在的行，从 “左边界” 列到 “右边界” 列（整行横向填充）。
• 操作：把当前要填的数字依次放在 “上边界行” 的每一列（从左到右），每放一个数字，填充数字加 1。
• 边界更新：上边界向下收缩 1 行（因为当前行已填满，下一轮填充要从更靠下的行开始）。

示例（以 n=4 为例）：

• 初始上边界 = 0 行，左边界 = 0 列，右边界 = 3 列；
• 填充 0 行：依次在 (0,0) 放 1、(0,1) 放 2、(0,2) 放 3、(0,3) 放 4；
• 填充后数字变为 5，上边界更新为 1 行。

2. 第二步：填充 “右边界”（从上到下）

• 目标区域：当前 “右边界” 所在的列，从 “上边界” 行到 “下边界” 行（整列纵向填充）。
• 操作：把当前要填的数字依次放在 “右边界列” 的每一行（从上到下），每放一个数字，填充数字加 1。
• 边界更新：右边界向左收缩 1 列（因为当前列已填满，下一轮填充要从更靠左的列开始）。

示例（n=4）：

• 当前右边界 = 3 列，上边界 = 1 行，下边界 = 3 行；
• 填充 3 列：依次在 (1,3) 放 5、(2,3) 放 6、(3,3) 放 7；
• 填充后数字变为 8，右边界更新为 2 列。

3. 第三步：填充 “下边界”（从右到左）

• 目标区域：当前 “下边界” 所在的行，从 “右边界” 列到 “左边界” 列（整行反向填充）。
• 操作：把当前要填的数字依次放在 “下边界行” 的每一列（从右到左），每放一个数字，填充数字加 1。
• 边界更新：下边界向上收缩 1 行（因为当前行已填满，下一轮填充要从更靠上的行开始）。

示例（n=4）：

• 当前下边界 = 3 行，右边界 = 2 列，左边界 = 0 列；
• 填充 3 行：依次在 (3,2) 放 8、(3,1) 放 9、(3,0) 放 10；
• 填充后数字变为 11，下边界更新为 2 行。

4. 第四步：填充 “左边界”（从下到上）

• 目标区域：当前 “左边界” 所在的列，从 “下边界” 行到 “上边界” 行（整列反向填充）。
• 操作：把当前要填的数字依次放在 “左边界列” 的每一行（从下到上），每放一个数字，填充数字加 1。
• 边界更新：左边界向右收缩 1 列（因为当前列已填满，下一轮填充要从更靠右的列开始）。

示例（n=4）：

• 当前左边界 = 0 列，下边界 = 2 行，上边界 = 1 行；
• 填充 0 列：依次在 (2,0) 放 11、(1,0) 放 12；
• 填充后数字变为 13，左边界更新为 1 列。

三、重复循环：完成内层填充

完成一轮 “上→右→下→左” 的填充后，四个边界已向内收缩，形成一个 “内层小矩阵”。重复执行第二步的 4 个填充步骤，直到填充数字超过 n2（所有位置都填满）。

示例（n=4 内层填充）：

• 第二轮填充时，上边界 = 1、下边界 = 2、左边界 = 1、右边界 = 2（内层 2×2 矩阵）；
• 先填上边界（1 行）：(1,1) 放 13、(1,2) 放 14；
• 再填右边界（2 列）：(2,2) 放 15；
• 再填下边界（2 行）：(2,1) 放 16；
• 此时数字已到 17（超过 42=16），填充结束。

四、最终结果：输出回型矩阵

填充完成后，按 “行优先” 顺序（从第 0 行到第 n−1 行，每行从第 0 列到第 n−1 列）依次呈现所有元素，即可得到回型矩阵。

示例（n=4 最终矩阵）：

1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7

由此，本题便完美解决，我们直接看详细注释版的完整代码：

#include <stdio.h>// 程序主函数，程序入口点
int main() {// 定义变量n，用于存储矩阵的阶数（n行n列）int n;// 提示用户输入矩阵大小（虽然代码里没写printf提示，但功能是读取n）// scanf函数从键盘读取一个整数，存储到变量n中// 例如用户输入4，就表示要生成4×4的回型矩阵scanf("%d", &n);// 定义一个20×20的二维数组matrix，用于存储生成的回型矩阵// 初始化所有元素为0（= {0}的作用）// 选择20×20是因为题目限制n≤19，足够容纳最大的矩阵int matrix[20][20] = {0};// 定义变量num，用于记录当前要填充到矩阵中的数字// 从1开始，因为回型矩阵是从1开始按顺序填充的int num = 1;// 定义四个边界变量，用于控制当前填充区域的范围// 想象成一个矩形的四条边，随着填充会不断向内收缩int top = 0;          // 上边界：当前需要填充的矩形的顶部行索引（初始为第0行）int bottom = n - 1;   // 下边界：当前需要填充的矩形的底部行索引（初始为最后一行n-1）int left = 0;         // 左边界：当前需要填充的矩形的左侧列索引（初始为第0列）int right = n - 1;    // 右边界：当前需要填充的矩形的右侧列索引（初始为最后一列n-1）// 循环填充矩阵，直到所有位置都被填满// 矩阵共有n×n个位置，当num超过n×n时表示所有位置都已填充while (num <= n * n) {// --------------------------// 第一步：填充上边界（从左到右）// --------------------------// for循环变量i表示列索引，从左边界left开始，到右边界right结束// 附加条件num <= n*n：防止在n为奇数时，最后一次循环重复填充中心元素for (int i = left; i <= right && num <= n * n; i++) {// 将当前数字num填充到矩阵的top行、i列位置matrix[top][i] = num;// 填充完成后，num自增1，准备填充下一个数字num++;}// 上边界这一行已经全部填充完成，将上边界向下移动一行（缩小填充范围）// 例如原来top=0，移动后top=1，下次就从第1行开始处理top++;// --------------------------// 第二步：填充右边界（从上到下）// --------------------------// for循环变量i表示行索引，从上边界top开始，到下边界bottom结束// 附加条件num <= n*n：同上，防止重复填充for (int i = top; i <= bottom && num <= n * n; i++) {// 将当前数字num填充到矩阵的i行、right列位置matrix[i][right] = num;// 填充完成后，num自增1num++;}// 右边界这一列已经全部填充完成，将右边界向左移动一列（缩小填充范围）// 例如原来right=3（n=4时），移动后right=2right--;// --------------------------// 第三步：填充下边界（从右到左）// --------------------------// for循环变量i表示列索引，从右边界right开始，到左边界left结束（反向遍历）// 附加条件num <= n*n：同上for (int i = right; i >= left && num <= n * n; i--) {// 将当前数字num填充到矩阵的bottom行、i列位置matrix[bottom][i] = num;// 填充完成后，num自增1num++;}// 下边界这一行已经全部填充完成，将下边界向上移动一行（缩小填充范围）// 例如原来bottom=3（n=4时），移动后bottom=2bottom--;// --------------------------// 第四步：填充左边界（从下到上）// --------------------------// for循环变量i表示行索引，从下边界bottom开始，到上边界top结束（反向遍历）// 附加条件num <= n*n：同上for (int i = bottom; i >= top && num <= n * n; i--) {// 将当前数字num填充到矩阵的i行、left列位置matrix[i][left] = num;// 填充完成后，num自增1num++;}// 左边界这一列已经全部填充完成，将左边界向右移动一列（缩小填充范围）// 例如原来left=0，移动后left=1left++;}// --------------------------// 输出回型矩阵// --------------------------// 外层for循环：遍历矩阵的每一行，i表示行索引（从0到n-1）for (int i = 0; i < n; i++) {// 内层for循环：遍历当前行的每一列，j表示列索引（从0到n-1）for (int j = 0; j < n; j++) {// 打印当前位置(i,j)的元素，后面加一个空格分隔printf("%d ", matrix[i][j]);}// 当一行的所有元素都打印完成后，换行printf("\n");}// 主函数返回0，表示程序正常结束return 0;
}

即如上，至此，本题大功告成。

BC134 蛇形矩阵：

其实这道题的思路和上一题回型矩阵差不多，我们先看题目：

题意分析：

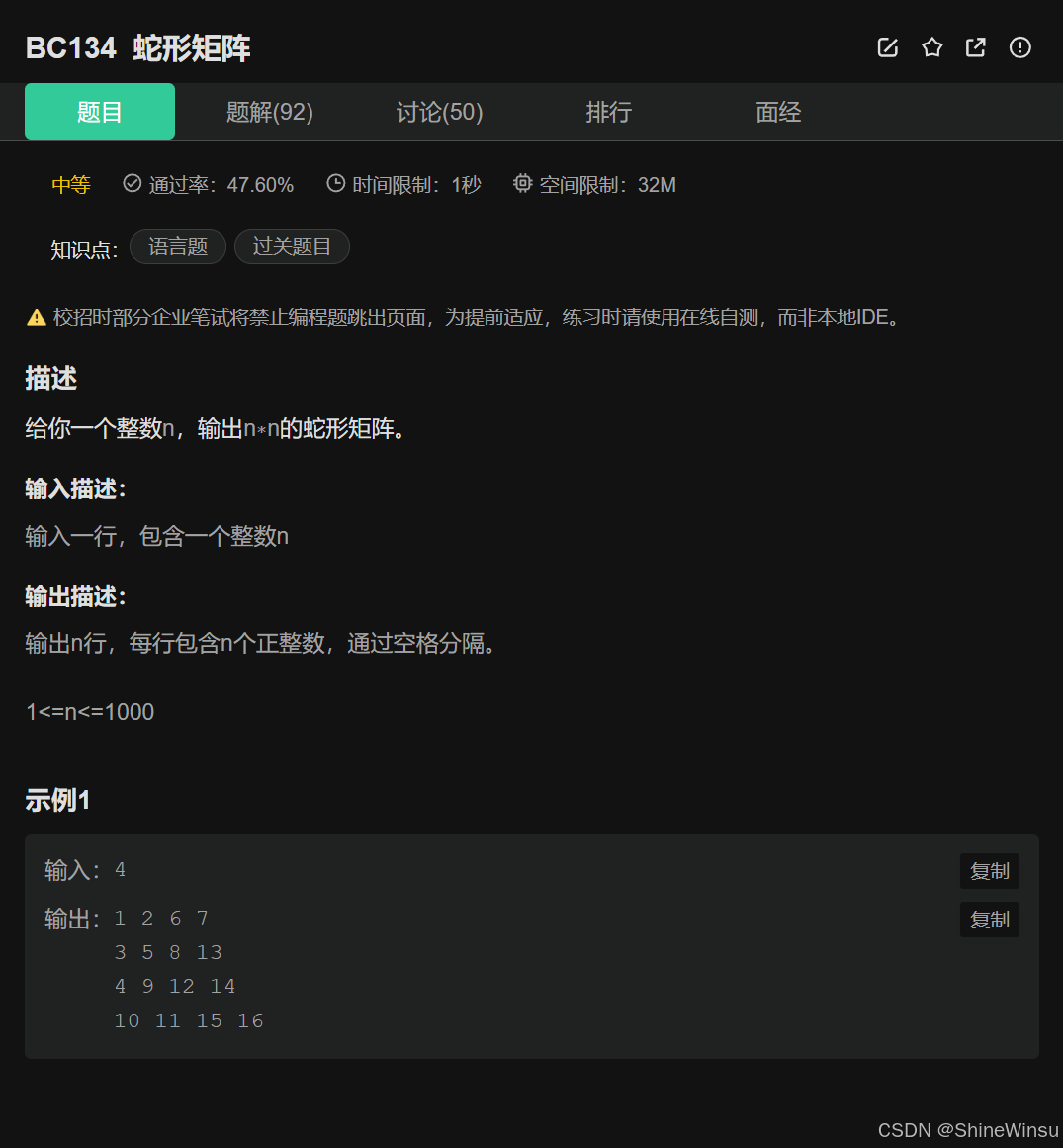
这道题要求我们根据输入的整数 n，生成一个 n×n 的蛇形矩阵。

输入输出分析

• 输入：一个整数 n（1≤n≤1000），表示要生成的蛇形矩阵的行数和列数。
• 输出：n 行，每行包含 n 个正整数，这些正整数按蛇形（斜向交替填充）的方式排列。

我们再观察一下题目所给示例中从小到大的数字所处的位置，它们是怎么安放的，我这里便直接给出答案：

蛇形矩阵的生成规则

蛇形矩阵的元素是按照斜向交替的顺序依次填充的。以示例输入 4 为例，输出的矩阵元素是从 1 开始，先沿右上到左下的对角线填充，再沿左下到右上的对角线填充，以此类推，直到填充完整个矩阵。

继续解答：

知道了题意之后，我们再看一下从小到大数字所处的坐标：

我们将矩阵的行从上到下编号为第 0 行、第 1 行、第 2 行、第 3 行，列从左到右编号为第 0 列、第 1 列、第 2 列、第 3 列，以下是每个元素对应的坐标（行，列）：

元素	坐标（行，列）
1	(0, 0)
2	(0, 1)
3	(1, 0)
4	(2, 0)
5	(1, 1)
6	(0, 2)
7	(0, 3)
8	(1, 2)
9	(2, 1)
10	(3, 0)
11	(3, 1)
12	(2, 2)
13	(1, 3)
14	(2, 3)
15	(3, 2)
16	(3, 3)

那么通过这个表格，不知道大家可看出什么规律来，考虑到本题难度确实较大，所以大家不必浪费时间于思考上，我们直接看规律：

一、填充方向规律

蛇形矩阵的填充是沿对角线交替方向进行的：

• 偶数次对角线（从第 0 条开始计数）：右上 → 左下（如填充元素 1→2→3；5→6→7 等，这里的 “次” 指对角线的序号）。
• 奇数次对角线：左下 → 右上（如填充元素 3→4→5；7→8→9 等）。

二、对角线的 “行 + 列” 和规律

每条对角线上的所有元素，行索引 + 列索引的和是固定的，且这个和等于 “对角线的序号”（从 0 开始）。

• 第 0 条对角线（和为 0）：仅元素 1，坐标 (0,0)（0+0=0）。
• 第 1 条对角线（和为 1）：元素 2（0+1=1）、3（1+0=1）。
• 第 2 条对角线（和为 2）：元素 6（0+2=2）、5（1+1=2）、4（2+0=2）。
• 第 3 条对角线（和为 3）：元素 7（0+3=3）、8（1+2=3）、9（2+1=3）、10（3+0=3）。
• 以此类推，第 k 条对角线的所有元素满足 行+列=k。

三、元素值的递增规律

元素值 严格递增（从 1 到 n2），且在同一条对角线上：

• 若对角线方向为 右上 → 左下：列索引递减，行索引递增，元素值也递增（如第 2 条对角线：6→5→4，列从 2→1→0，行从 0→1→2，值从 6→5→4 递减？这里看似矛盾，实际是 “对角线内的顺序” 和 “整体递增” 的结合 —— 整体上后一条对角线的元素值大于前一条，同一条对角线内的顺序是为了 “蛇形”）。
• 若对角线方向为 左下 → 右上：列索引递增，行索引递减，元素值递增（如第 3 条对角线：7→8→9→10，列从 3→2→1→0，行从 0→1→2→3，值从 7→8→9→10 递增）。

四、总结核心规律

蛇形矩阵的本质是按 “对角线分组”，每组对角线的 “行 + 列和” 固定，且填充方向在 “右上→左下” 和 “左下→右上” 之间交替，最终实现整体元素值从 1 到 n2 的蛇形递增。

知道了规律之后，本题的解决也就轻松一些了，下面我们看一下需要哪些步骤

步骤 1：理解 “对角线分组” 的核心逻辑

蛇形矩阵的每个元素，都属于某一条对角线，而这条对角线的标识是「行索引 + 列索引的和」（记为 count）。

• 例如 n=4 时：
  • 元素 1（坐标 (0,0)）：0+0=0，属于 count=0 的对角线。
  • 元素 2（坐标 (0,1)）、3（坐标 (1,0)）：0+1=1、1+0=1，属于 count=1 的对角线。
  • 元素 6（坐标 (0,2)）、5（坐标 (1,1)）、4（坐标 (2,0)）：0+2=2、1+1=2、2+0=2，属于 count=2 的对角线。
• 结论：第 count 条对角线的所有元素，都满足「行 + 列 = count」。

步骤 2：遍历所有对角线（count 从 0 到 2n−2）

因为矩阵是 n×n，行和列的最大索引是 n−1，所以最大的「行 + 列」和为 (n−1)+(n−1)=2n−2。因此，需要让 count 从 0 循环到 2n−2，覆盖所有对角线。

步骤 3：按 “奇偶方向” 填充每条对角线

蛇形矩阵的关键是填充方向交替：

• 当 count 为偶数时，填充方向是「右上 → 左下」（列索引递减，行索引递增）。
• 当 count 为奇数时，填充方向是「左下 → 右上」（列索引递增，行索引递增）。

子步骤 3.1：遍历对角线内的所有元素

对于当前 count，遍历矩阵中所有满足「行 i + 列 j = count」的位置 (i,j)。

子步骤 3.2：根据 count 奇偶性选择填充方式

• 若 count 是偶数：
  要实现「右上 → 左下」的填充，需要让列索引 j 递减，行索引 i 递增。此时，将元素值存入 arr[j][i]（因为 j 作为行、i 作为列时，j 从大到小、i 从小到大，等价于原坐标的列递减、行递增）。

  • 例如 count=2（偶数），满足 i+j=2 的坐标有 (0,2)、(1,1)、(2,0)：
    • 填充顺序为 (0,2)→(1,1)→(2,0)，对应存入 arr[2][0]、arr[1][1]、arr[0][2]（即值为 4、5、6）。

• 若 count 是奇数：
  要实现「左下 → 右上」的填充，需要让列索引 j 递增，行索引 i 递增。此时，直接将元素值存入 arr[i][j]（i 和 j 都从小到大，自然实现列递增、行递增）。

  • 例如 count=1（奇数），满足 i+j=1 的坐标有 (0,1)、(1,0)：
    • 填充顺序为 (0,1)→(1,0)，对应存入 arr[0][1]、arr[1][0]（即值为 2、3）。

子步骤 3.3：维护递增的填充值

使用变量 sum 从 1 开始，每填充一个位置，sum 就自增 1，保证矩阵值从 1 到 n2 递增。

步骤 4：输出蛇形矩阵

所有对角线填充完成后，通过两层循环遍历二维数组 arr：

• 外层循环遍历行（i 从 0 到 n−1）。
• 内层循环遍历列（j 从 0 到 n−1），打印每个位置的元素，并用空格分隔。
• 每行打印完毕后，输出换行符 \n，保证矩阵按行显示。

逻辑总结（以 n=4 为例，全程模拟）

1. count=0（偶数）：

   • 满足 i+j=0 的坐标：(0,0)。
   • 填充：arr[0][0] = 1（sum 从 1 开始）。

2. count=1（奇数）：

   • 满足 i+j=1 的坐标：(0,1)、(1,0)。
   • 填充：arr[0][1] = 2，arr[1][0] = 3（sum 变为 4）。

3. count=2（偶数）：

   • 满足 i+j=2 的坐标：(0,2)、(1,1)、(2,0)。
   • 填充：arr[2][0] = 4，arr[1][1] = 5，arr[0][2] = 6（sum 变为 7）。

4. count=3（奇数）：

   • 满足 i+j=3 的坐标：(0,3)、(1,2)、(2,1)、(3,0)。
   • 填充：arr[0][3] = 7，arr[1][2] = 8，arr[2][1] = 9，arr[3][0] = 10（sum 变为 11）。

5. count=4（偶数）：

   • 满足 i+j=4 的坐标：(1,3)、(2,2)、(3,1)。
   • 填充：arr[3][1] = 11，arr[2][2] = 12，arr[1][3] = 13（sum 变为 14）。

6. count=5（奇数）：

   • 满足 i+j=5 的坐标：(2,3)、(3,2)。
   • 填充：arr[2][3] = 14，arr[3][2] = 15（sum 变为 16）。

7. count=6（偶数）：

   • 满足 i+j=6 的坐标：(3,3)。
   • 填充：arr[3][3] = 16（sum 变为 17，但 n=4 时 n2=16，填充结束）。

8. 最终输出矩阵：

   1 2 6 7
   3 5 8 13
   4 9 12 14
   10 11 15 16
   

通过 “按对角线分组 → 奇偶方向交替填充 → 顺序输出” 的流程，即可生成符合要求的蛇形矩阵。

即如上，下面我们看一下详细注释版的完整代码：

#include <stdio.h>// 主函数：C程序的入口点，操作系统从这里开始执行代码
int main() {// 定义整数变量n，用于存储矩阵的阶数（行数和列数相等，都是n）// 例如n=3表示生成3×3的矩阵，n=4表示生成4×4的矩阵int n;// 调用scanf函数从标准输入（键盘）读取一个整数，存储到变量n中// &n表示取变量n的内存地址，确保输入的数值能正确存入n// 假设用户输入4，那么n的值将被设置为4scanf("%d", &n);// 定义一个n行n列的二维数组arr，用于存储最终生成的蛇形矩阵// 数组的大小由用户输入的n动态决定（C99及以上标准支持变长数组）// 例如n=4时，数组为arr[4][4]，包含16个元素（4×4）int arr[n][n];// 定义变量count：核心控制变量，代表"当前处理的对角线编号"// 蛇形矩阵的每条对角线具有特征：行索引 + 列索引 = count// 初始值为0，表示从第0条对角线开始处理int count = 0;// 定义变量sum：用于记录将要填充到矩阵中的数字，从1开始递增// 蛇形矩阵的填充规则是从1到n²依次填入，因此初始值为1int sum = 1;// while循环：遍历所有对角线，直到所有对角线处理完毕// 对于n×n的矩阵，对角线总数为2n-1条（编号从0到2n-2）// 例如n=4时，对角线编号为0~6（共7条，2×4-1=7）// 循环条件count < 2*n-1确保覆盖所有对角线while (count < 2 * n - 1) {// 外层for循环：遍历矩阵的所有行，i表示行索引（范围0~n-1）// 例如n=4时，i取值0、1、2、3for (int i = 0; i < n; i++) {// 内层for循环：遍历当前行的所有列，j表示列索引（范围0~n-1）// 例如n=4时，j取值0、1、2、3for (int j = 0; j < n; j++) {// 核心判断：当前位置(i,j)是否属于第count条对角线// 第count条对角线的所有元素必须满足"行索引+列索引=count"// 例如count=2时，(0,2)、(1,1)、(2,0)满足0+2=2、1+1=2、2+0=2if (i + j == count) {// 根据对角线编号count的奇偶性，决定填充方向和存储位置// 情况1：count为偶数（如0、2、4、6...）// 填充方向为"右上→左下"（列索引从大到小，行索引从小到大）// 此时通过arr[j][i]存储（交换i和j），实现反向填充if (count % 2 == 0) {arr[j][i] = sum;  // 将当前数字sum存入矩阵的(j,i)位置sum++;            // sum自增1，准备填充下一个数字}// 情况2：count为奇数（如1、3、5...）// 填充方向为"左下→右上"（列索引从小到大，行索引从小到大）// 此时直接通过arr[i][j]存储（保持i和j顺序），实现正向填充else {arr[i][j] = sum;  // 将当前数字sum存入矩阵的(i,j)位置sum++;            // sum自增1，准备填充下一个数字}}// 若i+j≠count，则当前位置不属于第count条对角线，不做处理}}// 当前对角线（count）处理完毕，count自增1，开始处理下一条对角线count++;}// 循环输出生成的蛇形矩阵// 外层for循环：遍历矩阵的每一行（行索引i从0到n-1）for (int i = 0; i < n; i++) {// 内层for循环：遍历当前行的每一列（列索引j从0到n-1）for (int j = 0; j < n; j++) {// 打印当前位置(i,j)的元素，后面加一个空格分隔，确保格式整齐printf("%d ", arr[i][j]);}// 一行打印完毕后，输出换行符，开始打印下一行printf("\n");}// 主函数返回0，表示程序正常执行结束return 0;
}

即如上，注意：本题难度确实大，而且对于大家今后的编程之路也没什么太实际的用处，所以大家不必耗费太多时间于其身上。

结语：以代码为舟，渡向更广阔的编程星河

当敲完蛇形矩阵最后一行输出代码的那一刻，我想和大家一样，心中既有 “攻克难题” 的释然，也有 “又进一寸” 的踏实 —— 这大概就是编程学习最迷人的地方：每一道题都是一座小小的山，攀上去时或许会因思路卡壳而焦虑，会因细节 bug 而烦躁，但当看到屏幕上正确输出的结果时，那种从 “未知” 到 “已知”、从 “困惑” 到 “通透” 的成就感，足以抵消所有过程的艰辛。

回顾这四篇关于二维数组的博客，我们从最基础的数组遍历开始，一步步走进杨辉三角的数学逻辑、回型矩阵的边界控制、蛇形矩阵的对角线规律。这些题目或许不是最难的，但它们像一把把钥匙，帮我们打开了 “用代码模拟现实逻辑” 的大门：杨辉三角让我们懂得，编程不只是敲键盘，更是对数学规律的转化与实现；回型矩阵教会我们，复杂问题可以拆解成 “上、右、下、左” 的简单步骤，边界收缩的思路能让螺旋填充变得清晰；蛇形矩阵则提醒我们，看似混乱的排列背后，总有 “行 + 列和固定” 这样的隐藏规律，耐心观察与归纳，往往是解题的第一步。

我知道，屏幕前的你或许和我一样，也曾在某个深夜对着代码皱眉 —— 可能是杨辉三角的递推公式卡了半小时，可能是回型矩阵的边界条件没控制好导致重复填充，也可能是蛇形矩阵的对角线方向搞反了，看着输出的混乱数字怀疑自己 “是不是不适合编程”。但请相信，这些瞬间都是编程学习的 “必经之路”。没有谁一开始就能轻松写出完美的代码，就像没有谁能一步登顶高山。那些看起来 “轻松解题” 的人，不过是在你看不见的地方，多试了几次循环条件，多画了几张坐标草图，多改了几版错误代码而已。

编程从来不是 “天才的游戏”，而是 “坚持者的战场”。它需要我们有 “拆解问题” 的耐心 —— 把回型矩阵的螺旋填充拆成四个方向的循环；需要我们有 “观察规律” 的细心 —— 从蛇形矩阵的坐标里找出 “行 + 列和固定” 的秘密；更需要我们有 “不怕犯错” 的勇气 —— 哪怕杨辉三角的格式对齐调了十次，哪怕回型矩阵的边界收缩错了五次，只要不放弃，每一次修改都是在靠近正确答案。

记得最开始学二维数组时，我也曾对着arr[i][j]和arr[j][i]的区别犯迷糊，对着双重循环的嵌套逻辑绕不清。但后来发现，所有的 “不熟练” 都能靠 “刻意练习” 化解：杨辉三角的递推公式，我在草稿纸上画了三行才理清组合数的关系；回型矩阵的边界控制，我用笔画了四个箭头标注 “上边界向下、右边界向左” 的步骤；蛇形矩阵的对角线填充，我把每个元素的坐标列成表格，才看出 “奇偶方向交替” 的规律。这些看似 “笨拙” 的方法，恰恰是编程学习中最扎实的路径 —— 没有捷径，唯有 “思考 - 实践 - 复盘” 的循环，才能让知识真正内化为自己的能力。

现在，二维数组的练习暂时告一段落，但这绝不是编程学习的终点。往后我们还会遇到更复杂的数据结构，比如链表、栈、队列；还会接触更抽象的算法思想，比如动态规划、贪心、回溯。但请记住，今天我们在二维数组中学到的 “拆解问题”“观察规律”“耐心调试” 的能力，会像一把把 “万能钥匙”，帮我们应对未来更多的挑战。就像杨辉三角的每一行都依赖上一行的积累，编程能力的提升也需要这样 “一步一个脚印” 的沉淀 —— 今天弄懂了回型矩阵的边界收缩，明天面对 “螺旋矩阵 II” 时就能更快上手；今天吃透了蛇形矩阵的对角线规律，未来遇到 “斜向遍历二叉树” 时也能举一反三。

最后，想和大家说：编程学习就像在一片广阔的星河里航行，我们每个人都是自己的舵手。有时会遇到 “思路枯竭” 的暗礁，有时会碰到 “bug 丛生” 的风浪，但只要我们保持对 “解决问题” 的热情，保持 “不断试错” 的勇气，保持 “总结复盘” 的习惯，就一定能让代码这叶小舟，载着我们驶向更广阔的远方。

或许你现在还在为一道题的解法发愁，或许你还在羡慕别人 “写代码又快又好”，但请不要着急。慢慢来，一步一步走，每一次成功运行的代码，每一次弄懂的知识点，都是在为你的编程之路添砖加瓦。未来的某一天，当你回头看时会发现，那些曾经让你头疼的二维数组题目，早已变成了你成长路上的 “垫脚石”。

愿我们都能在编程的世界里，保持好奇，保持热爱，保持 “啃硬骨头” 的韧劲 —— 下一道题，下一个知识点，下一个阶段，我们继续并肩前行，在代码的星河中，遇见更好的自己。