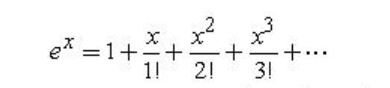python 数据拟合(线性拟合、多项式回归)
1.线性拟合
如图,有一组数据,似乎围绕着一条直线,上下浮动.
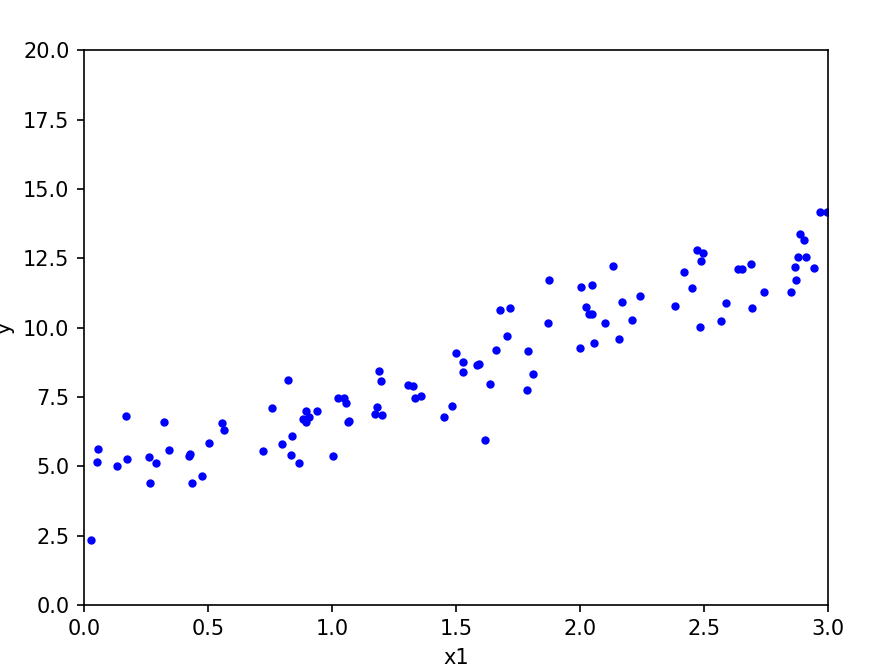
如何找到这条直线的表达式呢??
(数据来源的代码如下:
import numpy as np
import matplotlib.pyplot as plt# ============数据生成==================
# 生成特征数据 X:100个 [0,3) 区间的均匀分布随机数
X = 3 * np.random.rand(100) # np.random.rand生成[0,1)均匀分布,乘以3扩展到[0,3)# 生成目标数据 y:线性关系 y = 4 + 3X + 高斯噪声
y = 4 + 3 * X + np.random.randn(100) # np.random.randn生成标准正态分布噪声# 可视化原始数据
plt.plot(X, y, 'b.') # 蓝色点图
plt.xlabel('x1') # x轴标签
plt.ylabel('y') # y轴标签
plt.axis([0, 3, 0, 20]) # 设置坐标范围:x[0,3], y[0,20]
plt.show()
通过np.random随机生成噪音,环绕在 y = 4 + 3x 周围
)
==========================
方法一:正规方程法(Normal Equation)
通过解析解直接计算线性回归的最优参数,无需迭代。其核心是最小化均方误差(MSE)损失函数,通过数学推导得到闭式解(Closed-form Solution)。

代码:
# ===========方法一:正规方程法(直接计算最优参数)=============
X_b = np.c_[np.ones((100, 1)), X] # 添加偏置项列(全1列),将X转换为(100,2)矩阵
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) # 正规方程公式:(X^T X)^-1 X^T y# 可视化正规方程法的拟合结果
plt.plot(X, y, 'b.') # 原始数据
X_new = np.array([[0], [3]]) # 定义要预测的x范围(0到3)
X_new_b = np.c_[np.ones((2, 1)), X_new] # 为预测点添加偏置项
y_predict = X_new_b.dot(theta_best) # 计算预测值
plt.plot(X_new, y_predict, 'r-', linewidth=2, label='Normal Equation') # 绘制红色拟合线
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([0, 3, 0, 20])
plt.title('Normal Equation')
plt.legend()
plt.show()
print("正规方程法 - 截距:", theta_best[0].round(3), "斜率:", theta_best[1].round(3))
运行后,输出:
正规方程法 - 截距: 4.286 斜率: 2.797
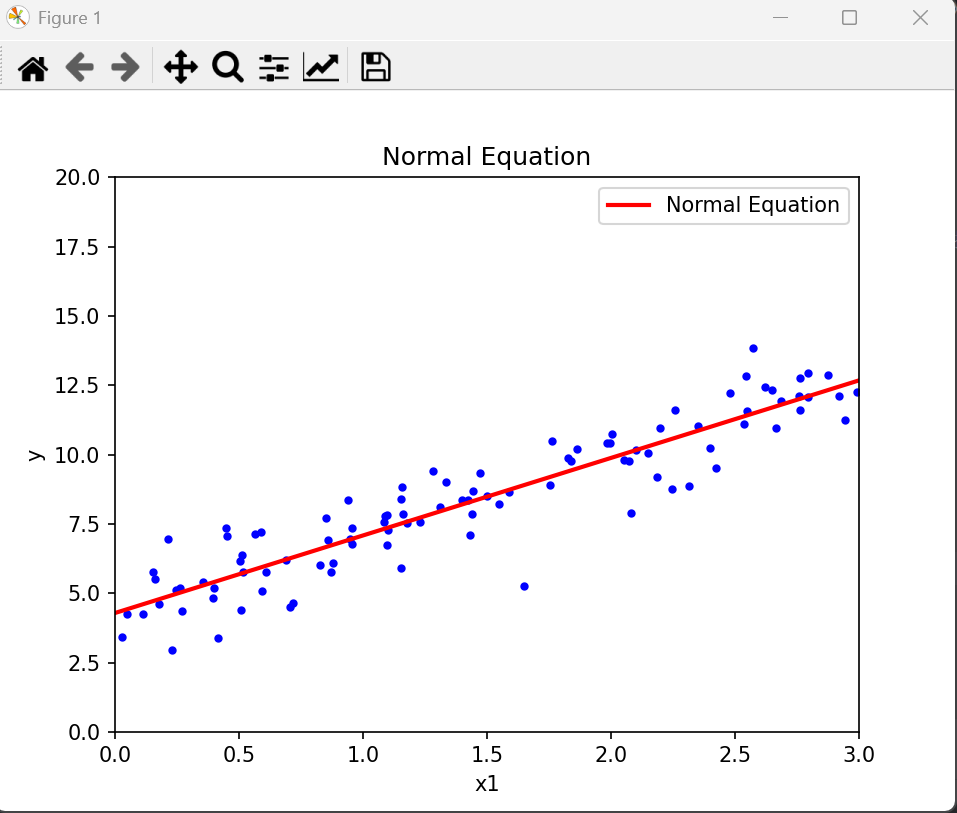
得到表达式 :y = 4.286 +2.797x
===================
方法二:梯度下降法(Gradient Descent)
通过迭代更新参数,沿着损失函数的负梯度方向逐步逼近最小值。其核心是不断修正参数,使得损失函数J(θ)最小化。

代码:
# ===========方法二:梯度下降法(迭代优化参数)=============
m = 100 # 样本数量
theta = np.random.randn(2, 1) # 随机初始化参数(2x1向量)
eta = 0.05 # 学习率(步长)
n_iterations = 2000 # 最大迭代次数
tolerance = 1e-4 # 收敛阈值(损失变化小于此值时停止)# 准备数据矩阵(与正规方程法相同)
X_b = np.c_[np.ones((100, 1)), X] # 添加偏置项
X_new = np.array([[0], [3]]) # 预测点
X_new_b = np.c_[np.ones((2, 1)), X_new] # 为预测点添加偏置项previous_loss = float('inf') # 初始化前一次损失为无穷大
for iteration in range(n_iterations):# 计算梯度(MSE损失函数的导数)gradients = (1 / m) * X_b.T.dot(X_b.dot(theta) - y.reshape(-1, 1)) # 【修正梯度计算】# 更新参数new_theta = theta - eta * gradients# 计算当前损失(MSE)current_loss = np.mean((X_b.dot(theta) - y.reshape(-1, 1)) ** 2)# 提前停止条件:损失变化小于阈值if abs(previous_loss - current_loss) < tolerance:breaktheta = new_theta # 更新参数previous_loss = current_loss # 记录当前损失# 可视化梯度下降法的拟合结果
plt.plot(X, y, 'b.') # 原始数据
y_predict = X_new_b.dot(theta) # 计算预测值
plt.plot(X_new, y_predict, 'g--', linewidth=2, label='Gradient Descent') # 绿色虚线
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([0, 3, 0, 20])
plt.title(f'Gradient Descent (eta={eta}, iterations={iteration})')
plt.legend()
plt.show()print("梯度下降法 - 截距:", theta[0][0].round(3), "斜率:", theta[1][0].round(3))运行后,输出:
梯度下降法 - 截距: 4.156 斜率: 2.869
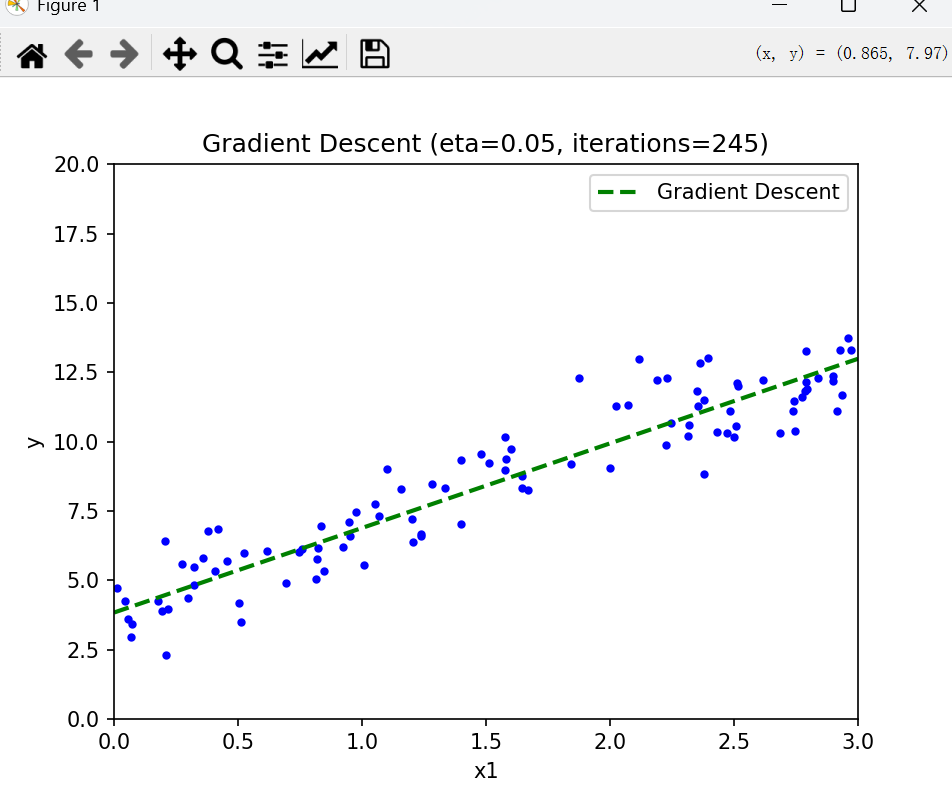
得到表达式 y= 4.156 +2.869x
线性拟合,完整代码:
import numpy as np
import matplotlib.pyplot as plt# ============数据生成==================
# 生成特征数据 X:100个 [0,3) 区间的均匀分布随机数
X = 3 * np.random.rand(100) # np.random.rand生成[0,1)均匀分布,乘以3扩展到[0,3)# 生成目标数据 y:线性关系 y = 4 + 3X + 高斯噪声
y = 4 + 3 * X + np.random.randn(100) # np.random.randn生成标准正态分布噪声# 可视化原始数据
plt.plot(X, y, 'b.') # 蓝色点图
plt.xlabel('x1') # x轴标签
plt.ylabel('y') # y轴标签
plt.axis([0, 3, 0, 20]) # 设置坐标范围:x[0,3], y[0,20]
plt.show()# =================拟合=============================# ===========方法一:正规方程法(直接计算最优参数)=============
X_b = np.c_[np.ones((100, 1)), X] # 添加偏置项列(全1列),将X转换为(100,2)矩阵
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) # 正规方程公式:(X^T X)^-1 X^T y# 可视化正规方程法的拟合结果
plt.plot(X, y, 'b.') # 原始数据
X_new = np.array([[0], [3]]) # 定义要预测的x范围(0到3)
X_new_b = np.c_[np.ones((2, 1)), X_new] # 为预测点添加偏置项
y_predict = X_new_b.dot(theta_best) # 计算预测值
plt.plot(X_new, y_predict, 'r-', linewidth=2, label='Normal Equation') # 绘制红色拟合线
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([0, 3, 0, 20])
plt.title('Normal Equation')
plt.legend()
plt.show()
print("正规方程法 - 截距:", theta_best[0].round(3), "斜率:", theta_best[1].round(3))# ===========方法二:梯度下降法(迭代优化参数)=============
m = 100 # 样本数量
theta = np.random.randn(2, 1) # 随机初始化参数(2x1向量)
eta = 0.05 # 学习率(步长)
n_iterations = 2000 # 最大迭代次数
tolerance = 1e-4 # 收敛阈值(损失变化小于此值时停止)# 准备数据矩阵(与正规方程法相同)
X_b = np.c_[np.ones((100, 1)), X] # 添加偏置项
X_new = np.array([[0], [3]]) # 预测点
X_new_b = np.c_[np.ones((2, 1)), X_new] # 为预测点添加偏置项previous_loss = float('inf') # 初始化前一次损失为无穷大
for iteration in range(n_iterations):# 计算梯度(MSE损失函数的导数)gradients = (1 / m) * X_b.T.dot(X_b.dot(theta) - y.reshape(-1, 1)) # 【修正梯度计算】# 更新参数new_theta = theta - eta * gradients# 计算当前损失(MSE)current_loss = np.mean((X_b.dot(theta) - y.reshape(-1, 1)) ** 2)# 提前停止条件:损失变化小于阈值if abs(previous_loss - current_loss) < tolerance:breaktheta = new_theta # 更新参数previous_loss = current_loss # 记录当前损失# 可视化梯度下降法的拟合结果
plt.plot(X, y, 'b.') # 原始数据
y_predict = X_new_b.dot(theta) # 计算预测值
plt.plot(X_new, y_predict, 'g--', linewidth=2, label='Gradient Descent') # 绿色虚线
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([0, 3, 0, 20])
plt.title(f'Gradient Descent (eta={eta}, iterations={iteration})')
plt.legend()
plt.show()print("梯度下降法 - 截距:", theta[0][0].round(3), "斜率:", theta[1][0].round(3))2.多项式回归
如图,有一组数据,近似一条曲线
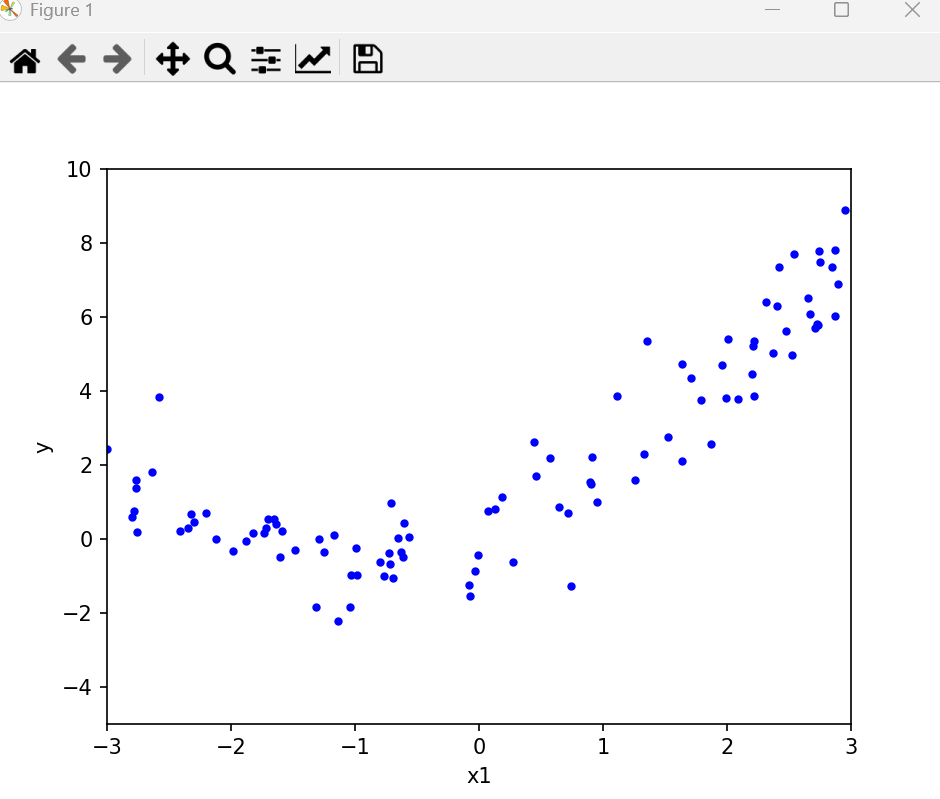
如何找到拟合的曲线?
(数据来源:
#===========生成随机数据(x,y)=============
m=100#生成100个点
X=6*np.random.rand(m,1)-3 #(x范围为 -3 ,3)y=0.5*X**2+X+np.random.randn(m,1) # y = 0.5x²+x#画出随机数据
plt.plot(X,y,'b.')
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([-3,3,-5,10])
plt.show()
)
多项式回归(Polynomial Regression):
通过将原始特征 X 转换为多项式特征,将非线性问题转化为线性问题,再使用线性回归模型拟合。
核心思想:用线性模型拟合非线性关系,通过增加高阶项扩展特征空间。
代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression#===========生成随机数据(x,y)=============
m=100#生成100个点
X=6*np.random.rand(m,1)-3 #(x范围为 -3 ,3)y=0.5*X**2+X+np.random.randn(m,1) # y = 0.5x²+x#画出随机数据
plt.plot(X,y,'b.')
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([-3,3,-5,10])
plt.show()#===============拟合========================
#PolynomialFeatures类用于将输入数据转换为多项式特征,其中degree参数指定了多项式的阶数(即最高次项),include_bias参数指定是否包括截距项(即常数项)。
poly_features = PolynomialFeatures(degree=2,include_bias=False)
#将转换后的特征矩阵存储在X_poly变量中
X_poly = poly_features.fit_transform(X)#线性回归模型对象lin_reg
lin_reg = LinearRegression()
#使用X_poly和y拟合了模型
lin_reg.fit(X_poly,y)
#首先生成100个在-3到3之间均匀分布的数字
# 然后将这些数字reshape为一个100x1的矩阵
X_new = np.linspace(-3,3,100).reshape(100,1)
#使用之前训练好的多项式特征转换器poly_features对X_new进行特征转换
X_new_poly = poly_features.transform(X_new)
#使用线性回归模型lin_reg对X_new_poly进行预测,得到预测结果y_new。
y_new = lin_reg.predict(X_new_poly)
plt.plot(X,y,'b.')
plt.plot(X_new,y_new,'r--',label='prediction')
plt.axis([-3,3,-5,10])
plt.legend()
plt.show()print("y = "+str(lin_reg.intercept_[0].round(3))+" + "+str(lin_reg.coef_[0][0].round(3))+"x"+" + "+str(lin_reg.coef_[0][1].round(3))+"x²")运行后输出:
y = 0.027 + 1.051x + 0.509x²
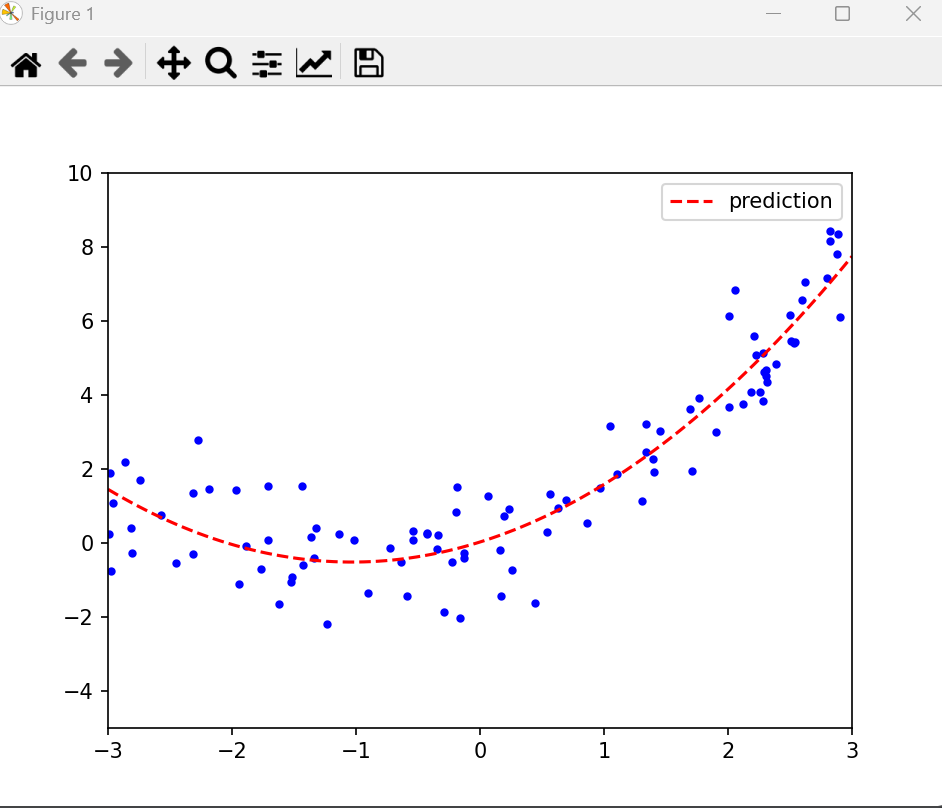
============
更换数据,
非常常见的y = e的x次方
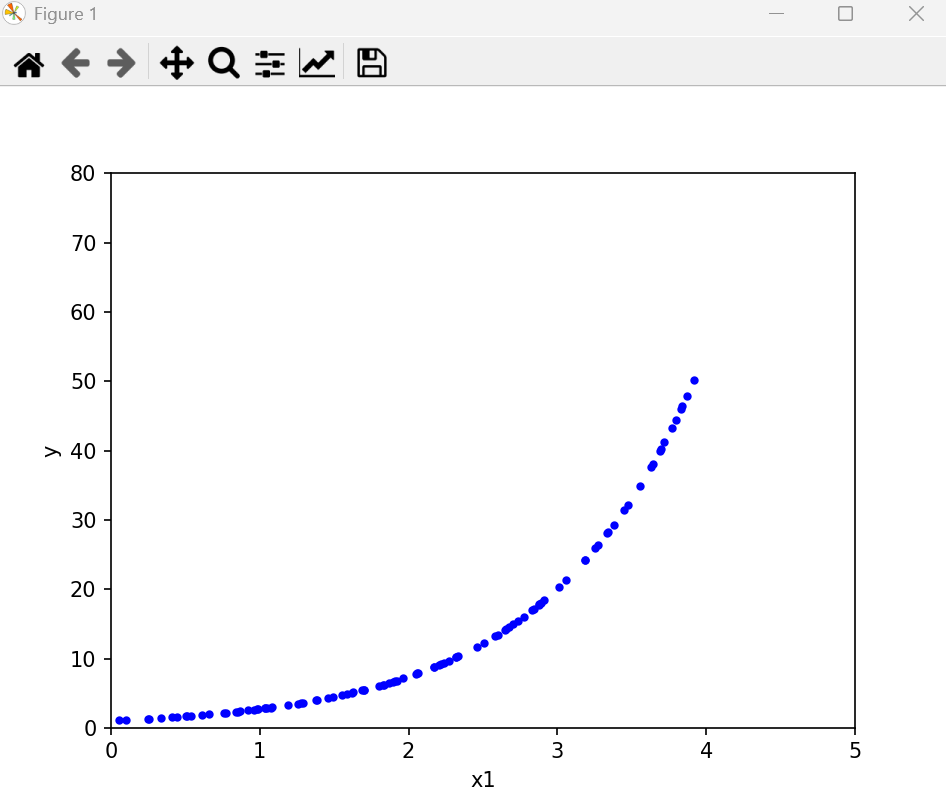
修改代码,多项式扩展到4次方
poly_features = PolynomialFeatures(degree=4,include_bias=False)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression#===========生成随机数据(x,y)=============
m=100#生成100个点X = 4*np.random.rand(m,1)y = 2.718**X#画出随机数据
plt.plot(X,y,'b.')
plt.xlabel('x1')
plt.ylabel('y')
plt.axis([0,5,0,80])
plt.show()#===============拟合========================
#PolynomialFeatures类用于将输入数据转换为多项式特征,其中degree参数指定了多项式的阶数(即最高次项),include_bias参数指定是否包括截距项(即常数项)。
poly_features = PolynomialFeatures(degree=4,include_bias=False)
#将转换后的特征矩阵存储在X_poly变量中
X_poly = poly_features.fit_transform(X)#线性回归模型对象lin_reg
lin_reg = LinearRegression()
#使用X_poly和y拟合了模型
lin_reg.fit(X_poly,y)
#首先生成100个在-3到3之间均匀分布的数字
# 然后将这些数字reshape为一个100x1的矩阵
X_new = np.linspace(0,5,100).reshape(100,1)
#使用之前训练好的多项式特征转换器poly_features对X_new进行特征转换
X_new_poly = poly_features.transform(X_new)
#使用线性回归模型lin_reg对X_new_poly进行预测,得到预测结果y_new。
y_new = lin_reg.predict(X_new_poly)
plt.plot(X,y,'b.')
plt.plot(X_new,y_new,'r--',label='prediction')
plt.axis([0,5,0,80])
plt.legend()
plt.show()print("y = "+str(lin_reg.intercept_[0].round(3))+" + "+str(lin_reg.coef_[0][0].round(3))+"x"+" + "+str(lin_reg.coef_[0][1].round(3))+"x**2"+" + "+str(lin_reg.coef_[0][2].round(3))+"x**3"+" + "+str(lin_reg.coef_[0][3].round(3))+"x**4")运行后:
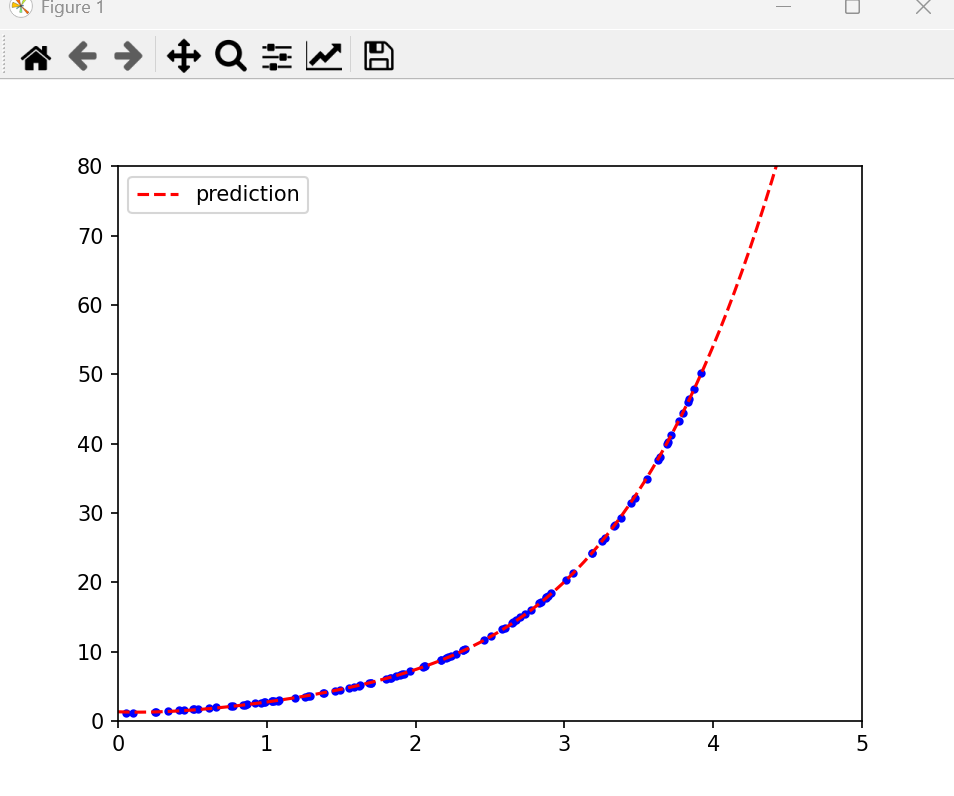
表达式:
y = 1.206 + -0.583x + 3.124x**2 + -1.366x**3 + 0.362x**4
提问:为什么和e的x次方的泰勒展开 不太一样呢?