【动态规划 | 路径问题】动态规划方法：解决路径问题的最佳策略

算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！
斐波那契数列模型

路径问题在计算机科学中有广泛的应用，如最短路径、最长路径以及各种约束条件下的路径优化问题。动态规划作为一种有效的算法策略，能够通过分治思想将复杂的路径问题分解为更小的子问题，从而提高计算效率。在本文中，我们将探讨动态规划方法如何成为解决路径问题的最佳策略，深入分析其在不同路径问题中的应用，以及如何通过合理设计状态转移方程来优化解法。

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏： 初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志 我自踏雪至山巅

62. 不同路径

【题目】：62. 不同路径

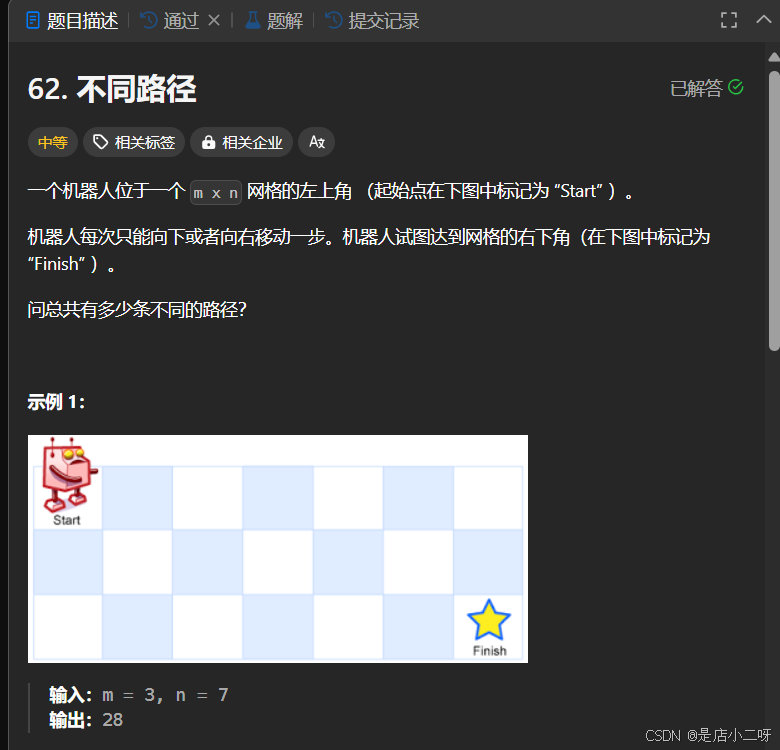
【算法思路】

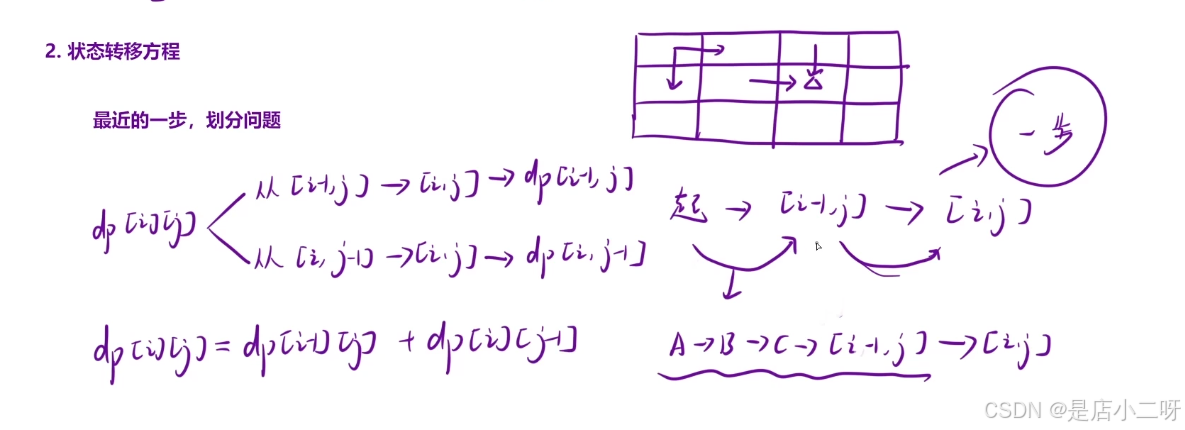
我们需要的是方法的数量，而不是单纯的一步。这里的‘方法数’指的是到达某个状态的不同方案数，而不是走了多少步。这个问题的关键在于如何表达选择的方法数，它不仅涉及到每步选择的方案数，还需要传递到下一步。

因此，我们需要重点关注当前状态与之前状态之间的关系，并明确其表达含义。通过找到合适的状态转移方程，我们可以更清晰地计算出每种情况的结果。在过程中，需要对不同情况进行讨论和分类，以避免潜在的错误或遗漏。

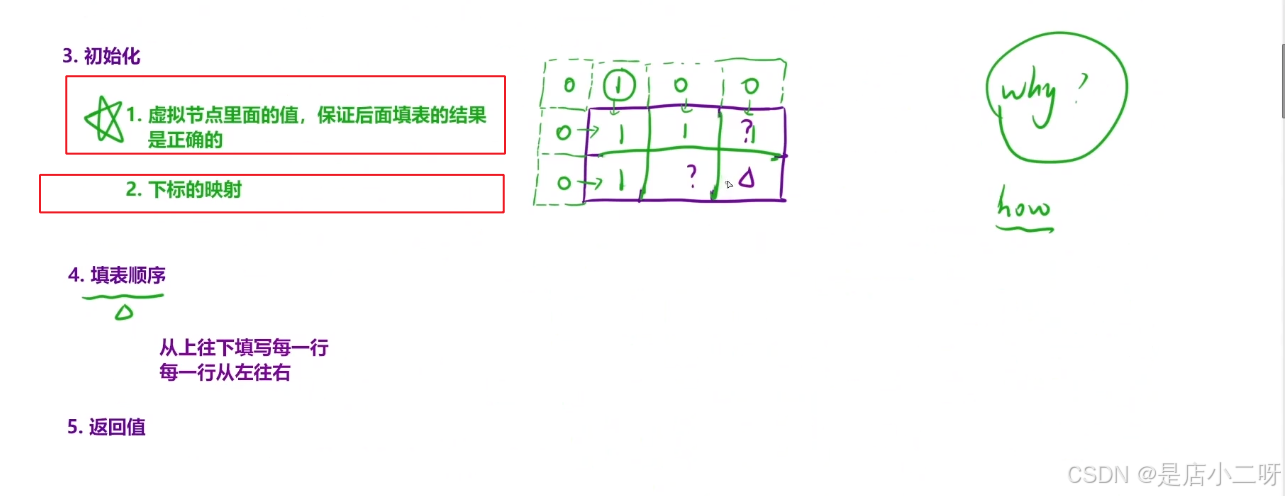
初始化有两种常用方法：

• 【方法一】：先为这些位置赋值，防止越界。
• 【方法二】：加载虚拟地址。

推荐使用第二种方法，因为它可以解决许多潜在问题。不过，在使用时需要特别注意下标的映射关系。

【代码实现】

class Solution {
public:int uniquePaths(int m, int n) {//1.创建dp表vector<vector<int>> dp(m + 1, vector<int>(n + 1));//2.特殊处理,初始化dp[0][1] = 1;//3.填表for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; //目前含有方法数return dp[m][n];}
};

---

63. 不同路径 II

【题目】：63. 不同路径 II

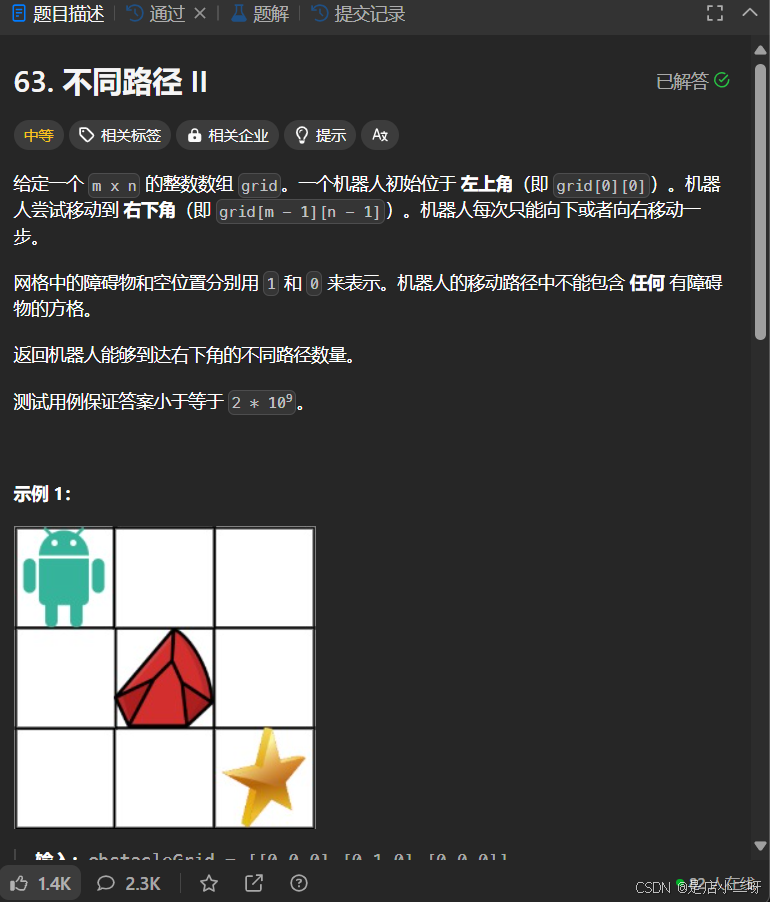
【算法思路】

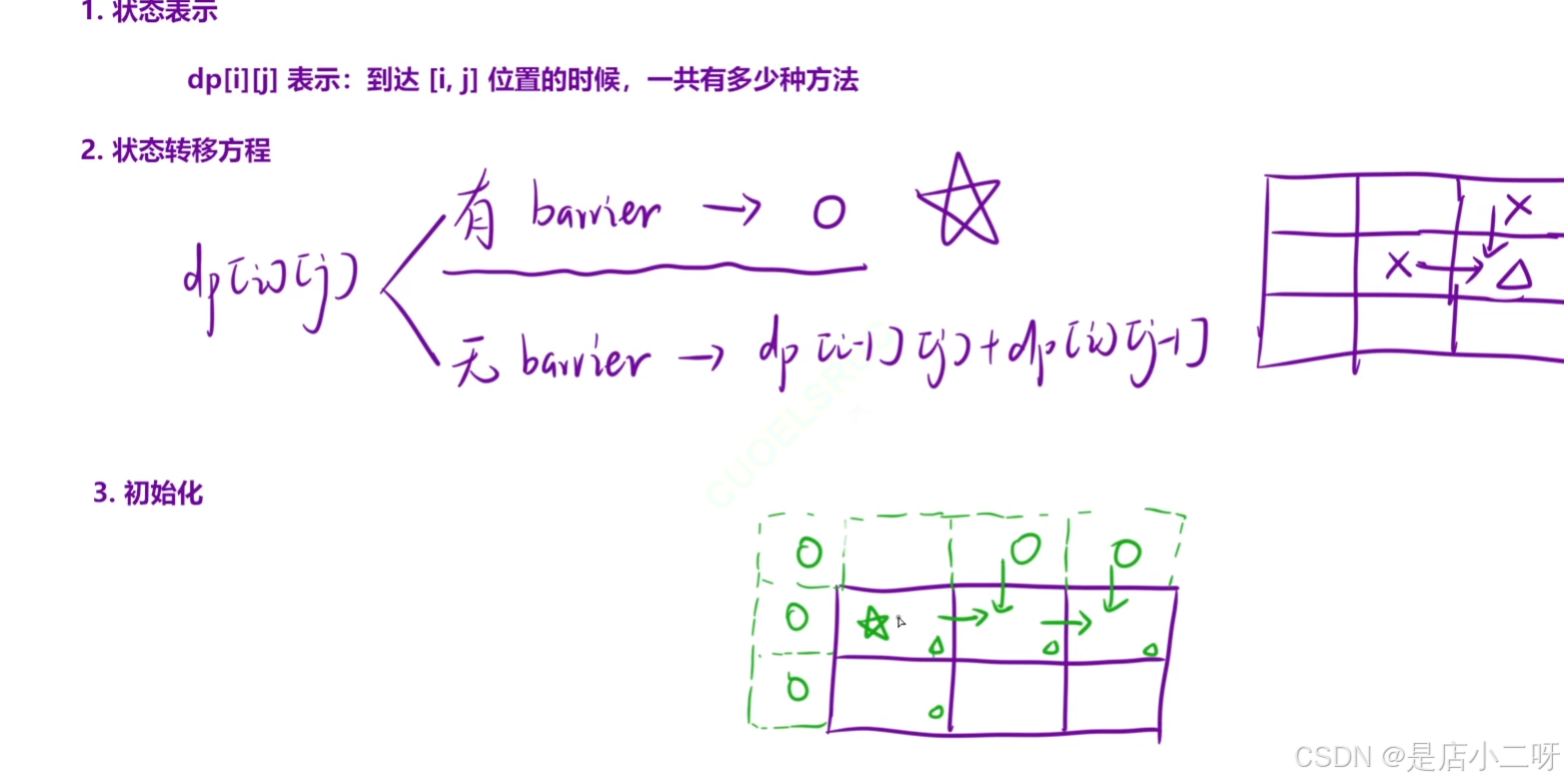
该题目与前一道题属于同类问题，主要区别在于添加了限制条件。对于路径问题，通常会想到使用动态规划（DP）来解决。在状态表示时，定义 dp[i][j] 为到达位置 (i, j) 的方法数。如果该位置为障碍物，则 dp[i][j] = 0。

如果当前位置的上方或左方为障碍物，也不影响结果，仍然可以计算为 0。需要注意的是，这道题涉及矩阵的下标映射，DP 需要从原矩阵的状态反推。

【代码实现】

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& ob) {int m = ob.size(), n = ob[0].size();//1.创建DP表vector<vector<int>> dp(m + 1, vector<int>(n + 1));//2.初始化dp[0][1] = 1;//3.填表，注意映射关系for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)if(ob[i - 1][j - 1] == 0)  dp[i][j] = dp[i][j - 1] + dp[i - 1][j];return dp[m][n];}
};

---

LCR 166. 珠宝的最高价值

【题目】：LCR 166. 珠宝的最高价值

【算法思路】

虽然动态规划（DP）解决问题的流程相似，但细节上有所不同，需要根据具体问题进行分析。对于本题，状态用 dp[i][j] 表示在位置 (i, j) 上能够取得的最大价值。状态转移方程由相邻状态推导得出，需重点关注状态之间的关系。在这里，转移方程为：
dp[i][j] = max(dp[i][j-1], dp[i-1][j]) + frame[i-1][j-1]

【代码实现】

class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m = frame.size(), n = frame[0].size();//1.创建dp表vector<vector<int>> dp(m + 1, vector<int>(n + 1));//2.填表for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]) + frame[i - 1][j - 1];return dp[m][n];}
};

---

931. 下降路径最小和

【题目】931. 下降路径最小和

【算法思路】

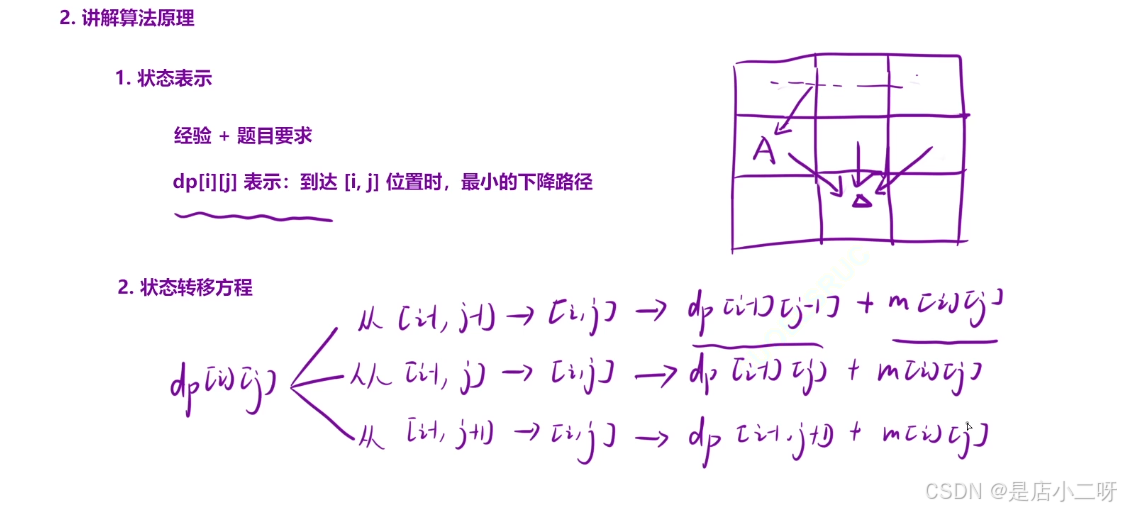
针对本题，通过样例分析可以得出，状态表示某个位置的‘当前下降路径的最小和’。根据题意和经验，我们可以推导出状态转移方程。最后，遍历所有状态并找到最小值作为最终答案。

【代码实现】

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();//1.创建dp表vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));//2.特殊初始化for(int cur = 0; cur < n + 2; cur++) dp[0][cur] = 0;//3.使用dp表for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)dp[i][j] = min(dp[i - 1][j],min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];//4.找到最小路径int minPath = INT_MAX;for(int index = 1; index <= n; index++) minPath = min(minPath, dp[n][index]);return minPath;}
};

---

64.最小路径和

【题目】：64. 最小路径和

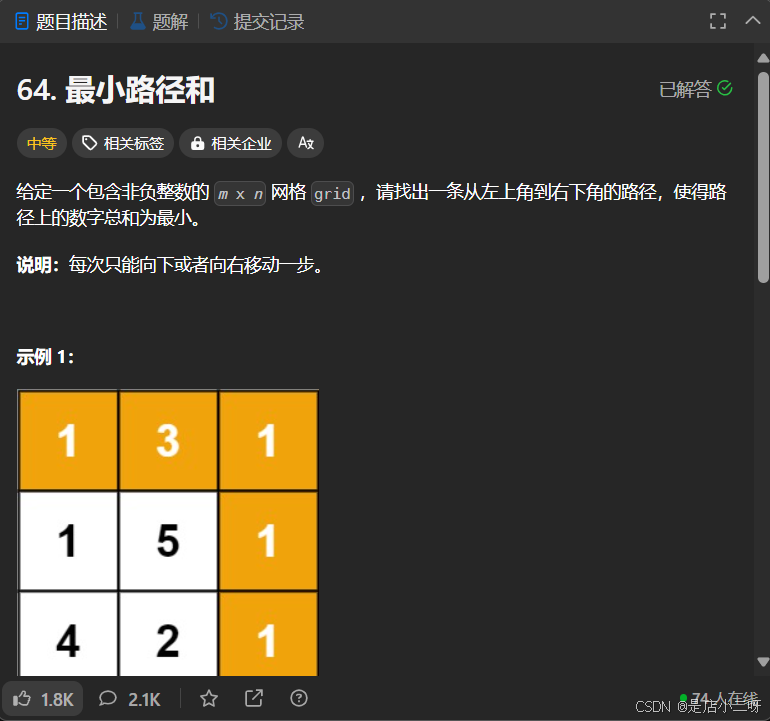
【算法思路】

该题是 LCR 166. 珠宝的最高价值 的变形题，dp[i][j] 的状态转移需要考虑最近一次‘数字总和最小’的最小值。

【代码实现】

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();//1.创建dp表vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));//2.特殊初始化dp[0][1] = dp[1][0] = 0;//3.填表for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];return dp[m][n];}
};

---

174. 地下城游戏

174. 地下城游戏

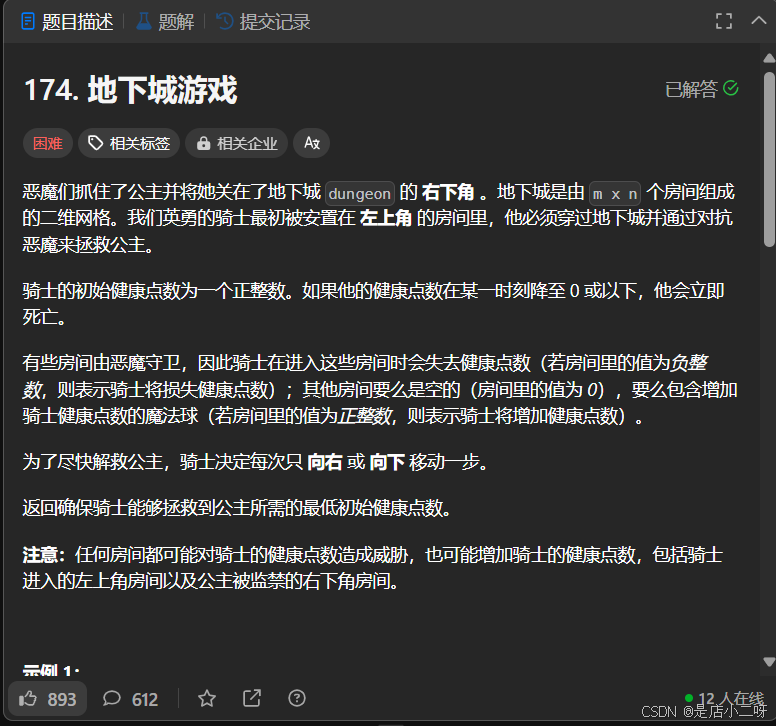
【算法思路】

对于DP问题，状态表示是最重要的一步，如果状态转移方程很难写出来，可能是状态表示出现了问题，而状态转移方程属于最难的一步。

【状态表示】

状态表示通常由经验和题目要求决定。

1.以某个位置为结尾，巴拉巴拉(本题不采用)

dp[i] [j] 表示：从起点开始，到达[i, j]位置时候，所需的最低初始健康点数

2.以以某个位置为起点，巴拉巴拉

dp[i] [j] 表示：从[i, j]位置开始，到达终点，所需的最低初始健康点数

注意：第一种方式不可用，因为到达某个位置的状态依赖于之前的状态和后续位置，前者存在不确定性，后者有后效性。因此，选择第二种方式，通过确定最小要求来明确状态。

【状态转移方程】

通过当前状态与相邻位置的状态建立联系，推导出状态转移方程。假设当前位置为 x，通过与右侧和下方位置的状态关系，确定最低要求。

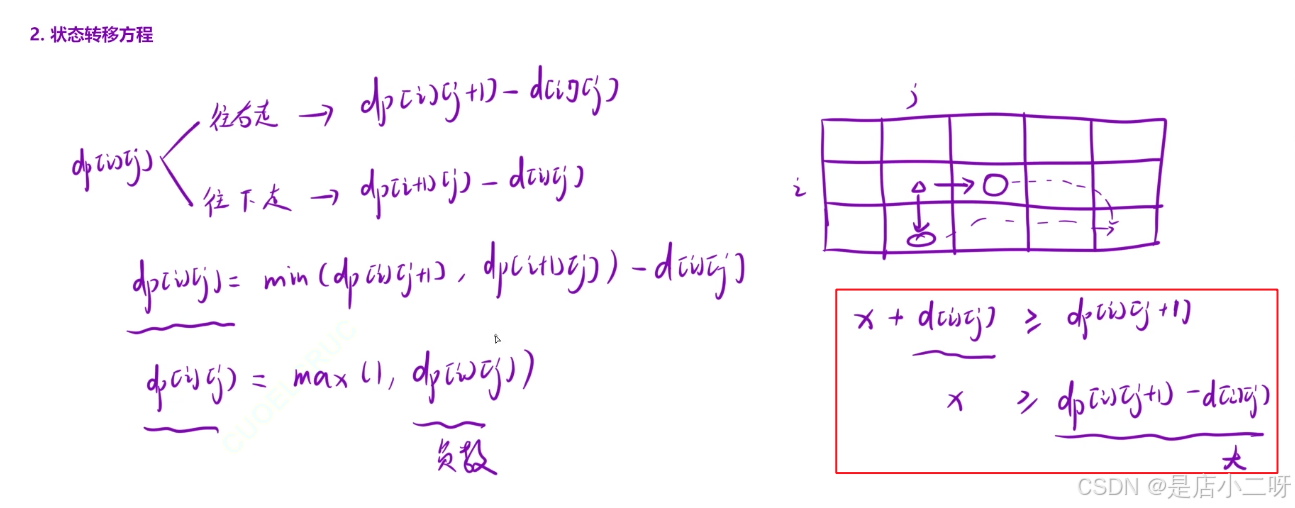
【细节问题】

如果 d[i][j] 过大，可能导致 dp[i][j] 为负数，违反题目要求。为了避免这种情况，需要进行特殊处理：dp[i][j] = max(1, dp[i][j]);

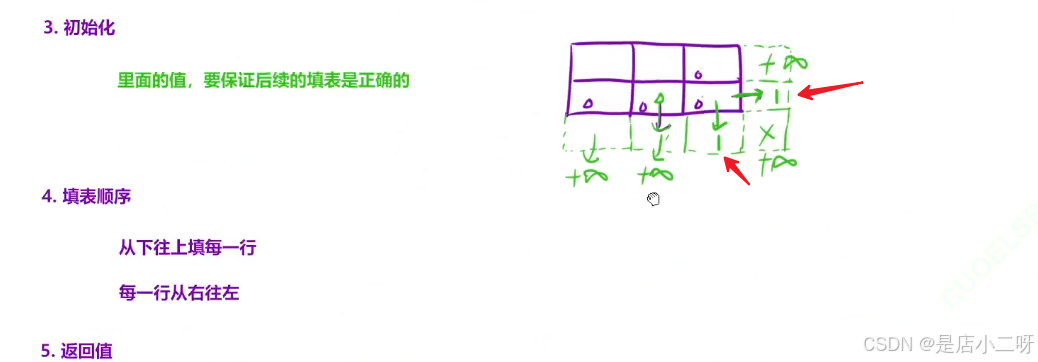
【代码实现】

class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m  = dungeon.size(), n = dungeon[0].size();//1.创建dp表vector<vector<int>> dp(m + 1,vector<int>(n + 1, INT_MAX));//2.初始化dp[m][n - 1] = dp[m - 1][n] = 1;//3.填表for(int i = m - 1; i >= 0; i--)for(int j = n - 1; j >= 0; j--){dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];dp[i][j] = max(1, dp[i][j]);//避免出现dungeon过大，导致初始血量为负数}return dp[0][0];}
};

快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！