当前位置：首页 > ops >正文

【学习笔记】深度学习-参数初始化

ops 2025/6/26 9:09:00

一、0初始化 🚫

	parameters = {}L = len(layers_dims)            # number of layers in the networkfor l in range(1, L):### 0初始化parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))###

会发生什么呢？对于任何输入 𝑥，神经元计算出来的值都是一样的
Zk = W(k,1)X1 + W(k,2)X2 + W(k,3)X3+…+ + W(k,n)Xn + bk
= 0X1 + 0X2 + … + 0*Xn + 0
= 0
【注】k表示第k层参数

结果就是：所有样本都预测为0
在这里插入图片描述

梯度为0，无论迭代多少轮，cost都没有下降，精确率和随机猜测差不多。

其实不止是0初始化，所有w都相同，b都相同的初始化也一样，都没有**“打破对称性”**（symmetry breaking），神经元的输出相同，激活值相同，它们的误差、梯度也都相同，于是：在之后的每一步梯度下降中，这两个神经元都会做一模一样的更新 → 永远无法分化。
所有神经元做一样的事，网络没有学习不同的特征，等价于你只用了一个神经元。

二、初始化过大🚫

    parameters = {}L = len(layers_dims)            # integer representing the number of layersfor l in range(1, L):### 参数大小*10parameters["W"+str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*10parameters["b"+str(l)] = np.zeros((layers_dims[l], 1))###

W1 = [[ 17.88628473   4.36509851   0.96497468][-18.63492703  -2.77388203  -3.54758979]]
b1 = [[0.][0.]]
W2 = [[-0.82741481 -6.27000677]]
b2 = [[0.]]Cost after iteration 0: inf
Cost after iteration 1000: 0.6244405061689552
Cost after iteration 2000: 0.5979643914272642
Cost after iteration 3000: 0.5637254162165872
Cost after iteration 4000: 0.5501640269883202
Cost after iteration 5000: 0.5444721253481484
Cost after iteration 6000: 0.5374632031142033
Cost after iteration 7000: 0.4777312272455887
Cost after iteration 8000: 0.39784053333340974
Cost after iteration 9000: 0.3934906959402653
Cost after iteration 10000: 0.3920338616006118
Cost after iteration 11000: 0.38928474137191077
Cost after iteration 12000: 0.3861583623847435
Cost after iteration 13000: 0.38498646217082794
Cost after iteration 14000: 0.38279729866923734

可以注意到，在iteration 0时，cost为inf，无穷大
这是因为：大权重 + 输入相乘后 z 会很大或很小，进入sigmoid函数：在这里插入图片描述

在这里插入图片描述
当输入在-6和6之外，输出就非常接近0或1了，以交叉熵损失函数来计算cost再反向传播为例：

当y=1时：如果预测值很小，如0.0001，则梯度通过链式法则反向传播后也会非常大：
-1/0.0001 = -10000

最终结果就是权重的更新量非常大，模型“跳得很猛”，甚至数值爆炸。
经过14000次迭代后，cost大约为0.38

三、He激活函数✅

为什么叫He激活？
“He 初始化”是因为它是由何恺明（Kaiming He）提出的，这位大神是 ResNet 的作者，现在在 Facebook AI Research 工作。他在 2015 年发表的论文：
“Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”
首次提出了这种针对 ReLU 的权重初始化方法。

代码

    parameters = {}L = len(layers_dims) - 1 # integer representing the number of layersfor l in range(1, L + 1):### 权重*(np.sqrt(2./layers_dims[l-1]))parameters["W"+str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*(np.sqrt(2./layers_dims[l-1]))parameters["b"+str(l)] = np.zeros((layers_dims[l], 1))###

为什么要乘以 √(2/n) ?
这是对 ReLU 的特别处理
在这里插入图片描述
这意味着它会截断一半的负值，输出的方差是输入方差的一半,每一层输出的方差都减半，最终结果是：

激活值越来越接近 0，网络的“信号”传不下去，导致：
1、梯度消失（反向传播时梯度也越来越小）
2、训练非常慢甚至完全停滞
3、模型无法收敛或性能极差
为了补偿这“损失的一半方差”，He 初始化就将权重初始化为：W = W*√(2/前一层的层数)

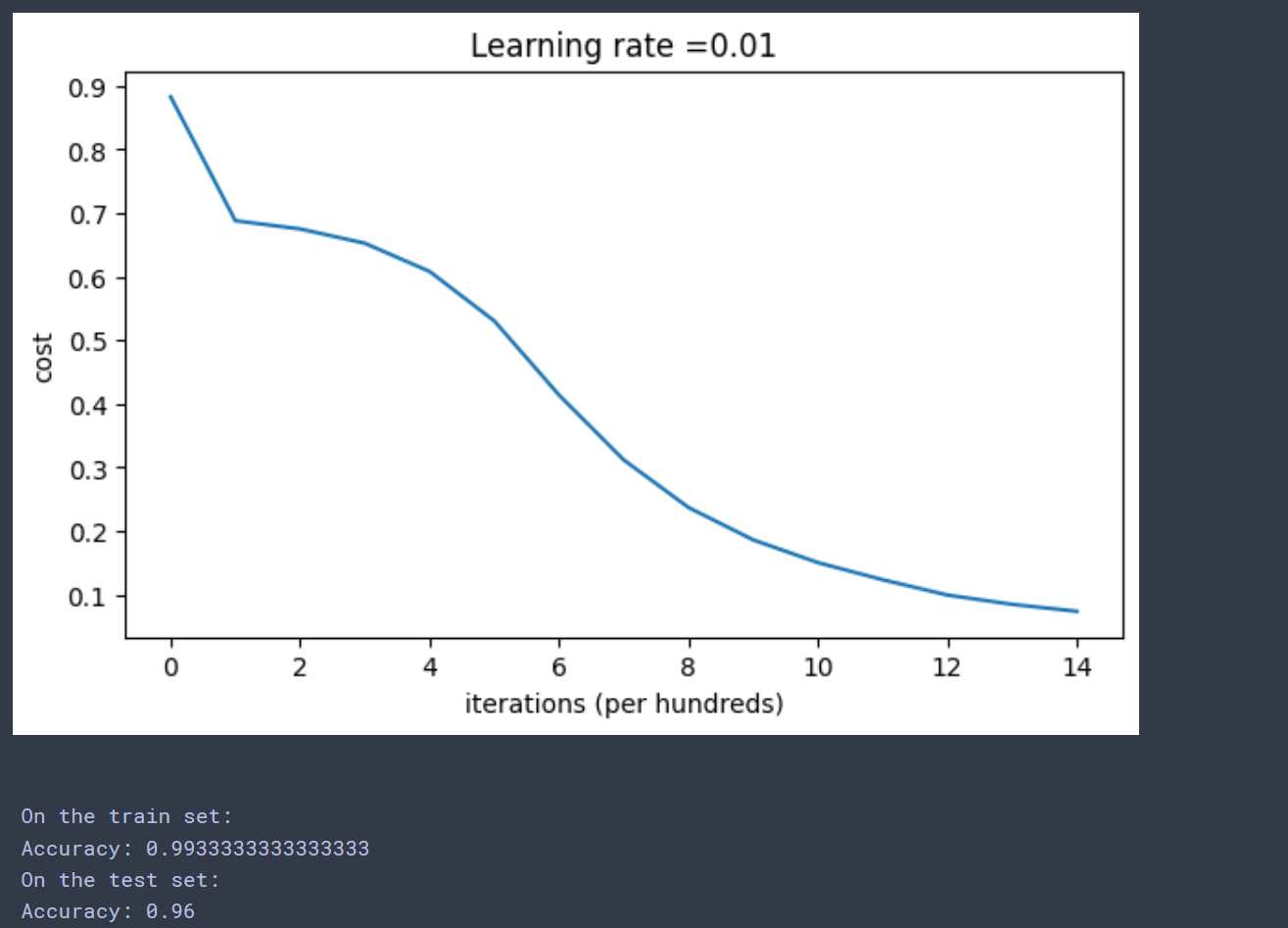
Cost after iteration 0: 0.8830537463419761
Cost after iteration 1000: 0.6879825919728063
Cost after iteration 2000: 0.6751286264523371
Cost after iteration 3000: 0.6526117768893807
Cost after iteration 4000: 0.6082958970572937
Cost after iteration 5000: 0.5304944491717495
Cost after iteration 6000: 0.41386458170717944
Cost after iteration 7000: 0.31178034648444414
Cost after iteration 8000: 0.23696215330322556
Cost after iteration 9000: 0.18597287209206836
Cost after iteration 10000: 0.1501555628037181
Cost after iteration 11000: 0.12325079292273546
Cost after iteration 12000: 0.09917746546525932
Cost after iteration 13000: 0.08457055954024277
Cost after iteration 14000: 0.07357895962677367

经过14000次迭代后cost为0.07，可见远优于前面的方法
在这里插入图片描述

四、Xavier 初始化✅

Xavier初始化（也叫Glorot初始化）是一种常见的权重初始化方法，它最初是由 Xavier Glorot 和 Yoshua Bengio 提出的，通常用于 sigmoid 或 tanh 激活函数的神经网络。
Xavier初始化的核心目标是确保神经网络每层的输入输出方差保持一致，从而避免激活值和梯度在网络中逐层衰减或爆炸的问题。

公式
Xavier初始化假设输入和输出的方差应该相等，根据方差传播规则：
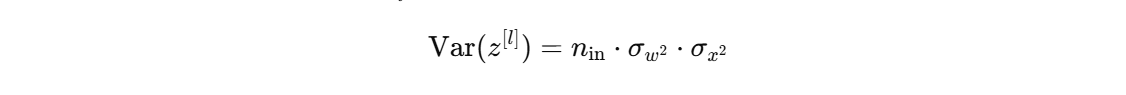
在这里插入图片描述

反向传播同理

因此初始化权重时，设定权重的方差为：
在这里插入图片描述

	parameters = {}L = len(layers_dims) - 1  # 总层数，减去1因为层数从0开始计数for l in range(1, L + 1):# Xavier 初始化，方差为 2 / (n_in + n_out)parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * np.sqrt(2. / (layers_dims[l-1] + layers_dims[l]))parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))return parameters

适用激活函数：Sigmoid、Tanh
Sigmoid和tanh的导数在其激活区间外（接近0或1）会非常小。这会导致反向传播时，梯度值非常小，从而导致梯度消失的问题。
Xavier初始化通过考虑输入和输出的层数来避免这种情况，让每层的输出方差保持稳定，减小梯度消失的风险。
Xavier 初始化在 ReLU 及其变体（如 Leaky ReLU）激活函数上表现不佳，容易导致方差逐层减小，最终可能导致梯度消失。

查看全文

http://www.xdnf.cn/news/12497.html