当前位置：首页 > news >正文

【工程开发】LLMC准确高效的LLM压缩工具（三）——AWQ算法量化

news 2025/8/6 18:26:41

AWQ算法过程与数学

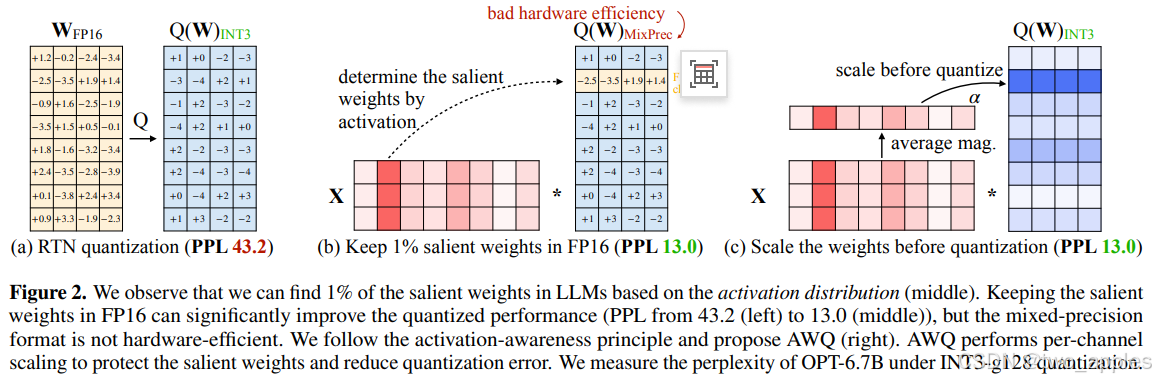
AWQ 的核心是激活感知的权重量化，即在权重量化过程中考虑激活值的影响，通过联合优化权重和激活值的量化过程，最小化量化误差对模型输出的影响。

基本步骤

数据收集与分析：收集模型的激活值和权重数据，分析这些数据以确定哪些权重对模型性能更为重要。同时，使用一组校准数据来估计激活值的统计特性1。
设计量化策略：根据激活值的分布和重要性，设计相应的量化策略，确定量化位宽（如 4 位、8 位等）和量化方式（如均匀量化、非均匀量化等）。
计算缩放因子：基于激活值的统计信息（如均值、最大值等），计算每个通道的缩放因子。这些缩放因子将用于在量化过程中调整权重和激活值的范围。
量化权重和激活值：使用确定的量化策略和缩放因子，对模型的权重和激活值进行量化，通常涉及将浮点数转换为定点数，以减少表示所需的位数。
量化后模型微调：由于量化会引入一定的误差，因此通常需要对量化后的模型进行微调，以恢复部分性能损失。微调过程中，可以使用原始数据集或一个小型校准集。
性能评估：评估量化后模型的性能，包括准确率、推理速度、功耗等指标。根据评估结果，调整量化策略和参数，以优化模型性能。
部署与集成：将量化后的模型部署到目标硬件平台上。根据硬件平台的特性，对模型进行进一步的优化和集成。

数学推导

量化模型：对于权重W，其量化表示为\(\hat{W}=round(W\times s_w)\)，其中\(s_w\)是权重的量化缩放因子，\(round()\)表示对数值进行四舍五入。激活值A也可以类似地进行量化，即\(\hat{A}=round(A\times s_a)\)，在 AWQ 中，会联合考虑权重和激活值的量化。
最小化输出误差：目标是最小化量化后的矩阵乘法输出\(\hat{Y}=\hat{A}\hat{W}\)与全精度输出\(Y = AW\)之间的误差，用公式表示为\(E = \vert\hat{Y}-Y\vert_F=\vert A\hat{W}-AW\vert_F\)，其中\(\vert\cdot\vert_F\)表示 Frobenius 范数。
解析求解量化参数：展开误差项\(E^2=\vert A\hat{W}-AW\vert_F^2=\sum_{i,j}(A_{ij}\hat{W}_{ij}-A_{ij}W_{ij})^2\)。为最小化上述误差，对\(s_w\)求导并设置导数为零，通过求解该方程，可以得到最优的\(s_w\)。
考虑激活值分布：由于激活值A的复杂分布，通常使用一组校准数据来估计激活值的统计特性，如均值、方差等。因此，误差最小化目标变为在考虑激活值分布的情况下，最小化E。例如，可以根据激活值的统计信息来调整量化缩放因子\(s_w\)和\(s_a\)，以更好地适应激活值的分布，减少量化误差。

通过上述步骤和数学推导，AWQ 算法能够在考虑激活值的基础上，对权重进行量化，从而在模型压缩和加速的同时，尽可能地保持模型的精度。

Frobenius 范数是什么？

Frobenius 范数是矩阵范数的一种，常用于数学和计算机科学等领域，特别是在矩阵计算和数值分析中。以下是其定义、性质及应用方面的介绍：

定义：对于一个\(m\times n\)的矩阵\(A=(a_{ij})\)，其 Frobenius 范数\(\vert\vert A\vert\vert_F\)定义为矩阵中所有元素的平方和的平方根，即\(\vert\vert A\vert\vert_F = \sqrt{\sum_{i = 1}^{m}\sum_{j = 1}^{n}\vert a_{ij}\vert^2}\)。例如，对于矩阵\(A=\begin{bmatrix}1&2\\3&4\end{bmatrix}\)，\(\vert\vert A\vert\vert_F=\sqrt{1^2 + 2^2 + 3^2 + 4^2}=\sqrt{30}\)。
性质
- 非负性：对于任意矩阵A，\(\vert\vert A\vert\vert_F\geq0\)，且\(\vert\vert A\vert\vert_F = 0\)当且仅当A是零矩阵。
- 齐次性：对于任意标量\(\alpha\)和矩阵A，有\(\vert\vert\alpha A\vert\vert_F=\vert\alpha\vert\vert\vert A\vert\vert_F\)。
- 三角不等式：对于任意两个同型矩阵A和B，\(\vert\vert A + B\vert\vert_F\leq\vert\vert A\vert\vert_F+\vert\vert B\vert\vert_F\)。
应用
- 衡量矩阵的大小：Frobenius 范数可以作为矩阵 “大小” 的一种度量，它类似于向量的欧几里得范数，在比较不同矩阵的规模或在优化问题中作为目标函数的一部分时很有用。
- 矩阵逼近：在矩阵逼近问题中，例如用低秩矩阵逼近一个给定的矩阵，Frobenius 范数常被用作衡量逼近误差的指标。
- 数值稳定性分析：在数值算法的稳定性分析中，Frobenius 范数可以用来分析矩阵运算过程中误差的传播和放大情况。

什么是对称优化？

对称优化在不同领域可能有不同的含义，以下从数学优化和模型量化两个角度为你解释：

数学优化领域：对称优化通常指利用问题本身所具有的对称性来简化优化过程或提高算法效率。例如，对于一些具有对称结构的函数或约束条件，通过利用其对称性，可以减少计算量、降低问题的复杂度，或者设计出更高效的求解算法。比如在某些线性规划问题中，如果系数矩阵具有对称性质，就可以利用这种对称性来优化求解过程，减少迭代次数或存储空间。
模型量化中的对称量化：这是一种针对数据分布进行的量化方式。在模型量化场景下，尤其是对神经网络中的权重和激活值进行量化时，对称量化假设数据分布是关于零点对称的。
- 原理：它将数据映射到有限的离散值集合中，通过设定一个量化范围和量化步长来实现。例如，对于 8 位对称量化，通常会将数据映射到 -128 到 127 之间的整数。
- 优点：计算相对简单，因为只需要确定一个量化参数（如量化范围），就可以根据对称性确定整个量化区间。
- 缺点：当数据分布并非严格对称，特别是存在非对称的长尾分布时，对称量化可能无法很好地表示数据的真实分布，从而导致较大的量化误差。这也是上述提到的传统量化方法的局限性之一，而 AWQ 算法就是为了解决这类问题而提出的激活感知的权重量化方法，它不再局限于对称量化，而是通过联合优化权重和激活值的量化过程来最小化量化误差对模型输出的影响。

对sw求导

虽然展开式中没有直接显式写出\(s_w\)，但\(\hat{\mathbf{W}}\)是与\(s_w\)相关的。根据之前量化模型的定义\(\hat{\mathbf{W}} = round(\mathbf{W}\times s_w)\)，\(\hat{\mathbf{W}}\)依赖于\(s_w\) ，所以\(\vert\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W})\vert_F^2\)实际上是关于\(s_w\)的复合函数，因此可以对\(s_w\)求导。以下是更详细说明：

1. 函数依赖关系

因为\(\hat{\mathbf{W}}\)由\(s_w\)决定，虽然在展开式\(\vert\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W})\vert_F^2 = \text{Tr}((\hat{\mathbf{W}} - \mathbf{W})^{\top}\mathbf{A}^{\top}\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W}))\)中没有直接写出\(s_w\)，但\(\hat{\mathbf{W}}\)的取值会随着\(s_w\)变化而变化。例如，当\(s_w\)增大时，\(\hat{\mathbf{W}} = round(\mathbf{W}\times s_w)\)的值也会相应改变（这里是经过四舍五入操作后的改变），进而导致\(\vert\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W})\vert_F^2\)的值改变。所以从本质上来说，\(\vert\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W})\vert_F^2\)是\(s_w\)的函数，只是依赖关系是间接的。

2. 求导过程

根据复合函数求导法则，当对\(\vert\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W})\vert_F^2\)关于\(s_w\)求导时，要先对\(\hat{\mathbf{W}}\)求导（这里因为\(\hat{\mathbf{W}} = round(\mathbf{W}\times s_w)\)，求导相对复杂一些，实际中可能需要根据四舍五入函数的特性做近似处理等），再乘以\(\hat{\mathbf{W}}\)对\(s_w\)的导数。当令\(\frac{\partial}{\partial s_w}\vert\mathbf{A}(\hat{\mathbf{W}} - \mathbf{W})\vert_F^2 = 0\)时，就是在寻找使得误差函数最小化的\(s_w\)的值，这个值对应的\(\hat{\mathbf{W}}\)能让量化后的权重与原始权重在与激活值\(\mathbf{A}\)进行矩阵乘法运算时，产生的误差最小。

一些问题

这里的校准数据具体形式是什么呢？是一组激活值？还是激活值+权重的组合？另外，如何得到这个校准数据集

校准数据的具体形式

校准数据通常是一组激活值。在神经网络中，激活值是输入数据经过神经元计算后的输出结果。之所以使用激活值作为校准数据，是因为 AWQ 算法关注的是激活值分布对权重量化的影响。通过分析激活值的统计特性（如均值、方差、最大值、最小值等），来更好地确定量化参数（如缩放因子\(s_w\) ），从而在权重量化时考虑激活值的情况，减少量化误差。一般不需要权重参与校准数据的组成，因为这里主要是为了刻画激活值分布，进而指导权重量化。

如何得到校准数据集

从原始训练数据中选取：从用于训练神经网络的原始数据集中，按照一定的规则抽取一部分数据样本。这些样本经过神经网络前向传播后，得到相应的激活值，这些激活值就构成了校准数据集。例如，可以随机抽取一定比例（如 1% - 5%）的训练样本，让它们通过神经网络，记录下在关键层（比如需要进行量化的层）产生的激活值。
独立的校准数据集：在一些情况下，会专门准备一个独立于训练集和测试集的校准数据集。这个数据集的分布尽量与训练数据的分布相似，但数据是不同的样本。比如在图像分类任务中，从与训练集同分布的其他图像数据中构建校准数据集，同样将这些图像输入神经网络，获取特定层的激活值作为校准数据。这样做的好处是可以避免校准过程对训练和测试过程产生干扰，并且能更专注地用于估计激活值的统计特性。

层级自适应量化 AWQ 通过分析各层对模型输出的敏感度，针对不同的层采用不同的量化比特位数，例如：对于对精度敏感的层，采用8位量化，而对于鲁棒性较高的层，采用4位或更低位数的量化。采用这种自适应策略可以在保证整体模型精度的情况下，进一步压缩模型大小。” 这里的层自适应量化具体又是怎么做的？

AWQ 中实现层级自适应量化，主要通过以下几个步骤：

分析层敏感度

确定分析指标：利用激活值来衡量权重的重要性，因为与大激活值对应的权重对模型输出影响更大。比如通过前向传播，统计各通道激活值的平均大小\(\bar{x}\) ，激活值大的通道被视为显著通道。
评估层敏感度：对神经网络的每一层进行分析，判断其对模型输出精度的影响程度。例如，靠近输入层的一些层可能对数据的初步特征提取很关键，改变其权重可能对后续层的处理产生较大影响，对精度相对敏感；而部分中间层可能具有一定的冗余性或鲁棒性，对量化的容忍度相对较高。

确定量化比特位数

设定量化策略：根据层的敏感度评估结果，为不同层分配不同的量化比特位数。一般对于对精度敏感的层，采用较高的量化比特位数，如 8 位量化，以保留更多信息，减少量化误差对模型输出的影响；对于鲁棒性较高的层，采用较低的量化比特位数，像 4 位或更低位数的量化，在可接受的精度损失范围内，实现模型压缩和计算加速。
灵活调整策略：策略并非固定不变，可根据具体模型特点、任务需求以及硬件资源等情况进行调整。比如在资源极度受限的边缘设备上，可能会适当降低更多层的量化比特位数；而对于对精度要求极高的任务，可能会放宽对一些层的量化程度。

执行量化操作的过程

按层量化：针对每一层，依据确定的量化比特位数进行量化处理。以 4 位量化为例，先确定量化范围（比如通过计算该层权重的最大值和最小值确定），再将权重映射到 4 位所能表示的数值范围内。对于按通道量化（AWQ 常见方式），会分别对每个通道的权重进行上述操作。
缩放显著权重（结合激活感知）：识别出需要保护的显著权重通道（如前所述，根据激活值大小确定）后，对这些显著权重进行缩放处理。将显著权重乘以一个缩放因子（\(s>1\)），相应地在计算时将输入除以相同的缩放因子，这样在量化过程中显著权重的相对误差被降低，同时确保模型计算结果的一致性。例如在对某一层进行量化时，先找出激活值大的通道对应的权重作为显著权重，对其缩放后再进行量化操作。

验证与优化

模型性能验证：对量化后的模型进行性能评估，通过在验证集或测试集上进行推理，计算准确率、损失值、困惑度（语言模型场景）等指标，观察模型在不同层采用不同量化策略后的精度变化情况。
调整量化策略：根据验证结果，若发现某些层的量化导致模型精度下降过多，可针对性地调整这些层的量化比特位数或量化方式；或者重新分析层的敏感度，优化显著权重的识别和缩放因子等参数，再次进行量化，不断迭代以在模型压缩和精度保持之间找到更好的平衡。

困惑度

困惑度（Perplexity）常用于机器学习，特别是自然语言处理领域，用于衡量一个模型对文本数据的预测能力，直观上表示模型对数据 “不确定” 的程度。从数学角度，对于给定的单词序列\(w_1, w_2, \ldots, w_n\)，以及测试数据集D，困惑度的计算公式为： \(perplexity(D)=\sqrt[N]{\prod_{i = 1}^{N}\frac{1}{P(w_i|w_1, w_2, \ldots, w_{i - 1})}}\) 其中，N表示测试数据集D中的单词数量，\(P(w_i|w_1, w_2, \ldots, w_{i - 1})\)表示在已知前\(i - 1\)个单词的情况下，模型预测第i个单词的条件概率。

简单来说，困惑度衡量的是模型在预测下一个词时的不确定性。困惑度越低，说明模型对数据的预测更加准确，即模型更 “确信” 它的预测；困惑度越高，表示模型对数据的预测更加不确定，表现越差。例如，若模型的困惑度为1 ，意味着模型完全确定地正确预测所有单词（理论最优情况）；若困惑度大于1 ，则表明模型存在一定的不确定性或错误，且数值越大，对序列的预测不确定性越高，质量越差。

也可以将困惑度理解为模型平均需要 “猜多少次” 才能选中正确词语。假设困惑度\(PPL = 20\)，意味着模型平均要在20个候选词中找到正确答案。

在衡量大模型量化效果方面的适用性

自然语言处理任务：在诸如文本生成、机器翻译、语音识别等自然语言处理任务中，困惑度是一个较为有效的衡量大模型量化效果的指标。因为这些任务中，模型需要基于前文内容预测下一个词（或符号），量化前后如果困惑度变化较小，说明模型对文本的预测能力受量化影响不大，即模型在这些任务上较好地保持了性能；若困惑度大幅上升，则表示量化带来了较大的精度损失，模型预测准确性变差。例如在文本生成任务中，量化前模型生成的文本连贯、合理，量化后困惑度显著升高，可能生成的文本就会出现语义不连贯、用词不合理等问题。
其他非语言类任务：对于图像识别、目标检测等非自然语言处理任务，困惑度通常不直接适用。这些任务有各自专门的评估指标，如图像识别中的准确率、召回率、F1 值等，目标检测中的平均精度均值（mAP）等。因为这些任务的输出并非是基于语言序列的预测，而是对图像中目标的分类、定位等，困惑度无法准确衡量模型在这些任务上量化前后的性能变化。但如果大模型在这些任务中涉及到文本相关的辅助生成（如生成图像描述等），在这部分文本生成环节可以用困惑度辅助评估量化效果。

代码解析

1. 导入模块

import gc
import osimport torch
import torch.distributed as dist
import torch.nn as nn
from loguru import loggerfrom llmc.utils.registry_factory import ALGO_REGISTRYfrom .base_blockwise_quantization import BaseBlockwiseQuantization
from .utils import is_fp8_supported_gpuif is_fp8_supported_gpu():from .kernel import weight_cast_to_bf16, weight_cast_to_fp8logger.info('import kernel successful.')
else:from .quant import weight_cast_to_bf16, weight_cast_to_fp8logger.info('import quant successful.')from .module_utils import (_LLMC_LINEAR_TYPES_, _LLMC_LN_TYPES_,_TRANSFORMERS_LINEAR_TYPES_,_TRANSFORMERS_LN_TYPES_, FakeQuantLinear)
from .utils import check_do_quant, check_w_only, get_aquantizer, get_wquantizer

gc：用于垃圾回收，可手动释放不再使用的内存。
os：提供了与操作系统交互的功能。
torch：PyTorch 深度学习库。
torch.distributed：用于分布式训练。
torch.nn：包含了构建神经网络的基础模块。
loguru：用于日志记录。
ALGO_REGISTRY：从llmc.utils.registry_factory导入的算法注册器。
BaseBlockwiseQuantization：自定义的基类，用于块级量化。
根据 GPU 是否支持 FP8 格式，从不同模块导入weight_cast_to_bf16和weight_cast_to_fp8函数。
从module_utils导入一些线性层和层归一化层的类型定义以及FakeQuantLinear类。
从utils导入一些工具函数。

2. `Awq`类定义

@ALGO_REGISTRY
class Awq(BaseBlockwiseQuantization):def __init__(self, model, quant_config, input, padding_mask, config):super().__init__(model, quant_config, input, padding_mask, config)special_config = self.quant_config.get('special', {})self.trans = special_config.get('trans', True)self.trans_version = special_config.get('trans_version', 'v2')self.save_scale = special_config.get('save_scale', False)self.awq_bs = special_config.get('awq_bs', None)self.save_mem = special_config.get('save_mem', True)

Awq类继承自BaseBlockwiseQuantization，并通过ALGO_REGISTRY进行注册。
__init__方法初始化类的实例，接收模型、量化配置、输入、填充掩码和配置作为参数。
从量化配置的special部分获取一些特殊配置，如是否进行变换、变换版本、是否保存缩放因子、批量大小和是否节省内存等。

3. 类方法

`scaling_weight`方法

@torch.no_grad()
def scaling_weight(self, w, scales, is_gqa):if is_gqa:scales_tmp = self.repeat_gqa_scales(scales)else:scales_tmp = scalesw.mul_(scales_tmp.view(1, -1))return w

该方法用于对权重进行缩放。
如果是 GQA（Grouped Query Attention），则调用repeat_gqa_scales方法对缩放因子进行处理。
最后将权重与缩放因子相乘并返回。

`get_weight_scale`方法

def get_weight_scale(self, layers_dict):layers = list(layers_dict.values())total_scale = Nonefirst_layer_name = list(layers_dict.keys())[0]wquantizer = get_wquantizer(self.block_idx,first_layer_name,self.mix_bits_map,self.quantizer_mix_bits,self.wquantizer,)for idx, _m in enumerate(layers):if _m.weight.data.dtype == torch.float8_e4m3fn:weight = weight_cast_to_bf16(_m.weight.data,_m.weight_scale_inv.data).to(torch.bfloat16)else:weight = _m.weight.data.clone()org_shape = weight.shapereshaped = wquantizer.reshape_tensor(weight)abs_weights = reshaped.abs()max_vals = abs_weights.amax(dim=1, keepdim=True)layer_scale = abs_weights.div_(max_vals)layer_scale = layer_scale.view(org_shape)if total_scale is None:total_scale = layer_scale.mean(0)else:total_scale.add_(layer_scale.mean(0))del weight, reshaped, abs_weights, max_vals, layer_scaletorch.cuda.empty_cache()return total_scale.div_(len(layers))

该方法用于计算权重的缩放因子。
遍历layers_dict中的所有层，根据层的权重数据类型进行处理。
对权重进行重塑、取绝对值、求最大值等操作，计算每层的缩放因子。
最后将所有层的缩放因子求平均并返回。

`get_act_scale`方法

def get_act_scale(self, x):if x.shape[0] == self._bs:return x.abs().view(-1, x.shape[-1]).mean(0)else:batch_means = []b_num = x.shape[0] // self._bsfor num in range(b_num):batch_x = x[num * self._bs:(num + 1) * self._bs]batch_mean = batch_x.abs().view(-1, batch_x.shape[-1]).mean(0)batch_means.append(batch_mean)final_mean = sum(batch_means) / len(batch_means)return final_mean

该方法用于计算激活值的缩放因子。
如果输入的批量大小等于预设的批量大小，则直接计算激活值的绝对值的平均值。
否则，将输入按批量大小分割，分别计算每个批量的激活值的绝对值的平均值，最后求平均并返回。

`get_scales`方法

@torch.no_grad()
def get_scales(self, prev_op, x, w_max, is_gqa, ratio):if is_gqa:x_tmp = prev_op(x)w_tmp = self.get_weight_scale({'prev_op': prev_op})else:x_tmp = xw_tmp = w_maxx_tmp = self.get_act_scale(x_tmp)if self.trans_version == 'v1' and not is_gqa:scales = ((x_tmp.pow(ratio) / w_tmp.pow(1 - ratio)).clamp(min=1e-4).view(-1))elif self.trans_version == 'v2' or is_gqa:scales = x_tmp.pow(ratio).clamp(min=1e-4).view(-1)scales = scales / (scales.max() * scales.min()).sqrt()return scales

该方法用于计算缩放因子。
如果是 GQA，则对输入进行前一层操作，并计算前一层的权重缩放因子。
根据变换版本和是否为 GQA，使用不同的公式计算缩放因子。
最后对缩放因子进行归一化处理并返回。

`inspect_module_forward`方法

def inspect_module_forward(self, x, inspect_module, kwargs):if self._bs == x.shape[0]:with torch.no_grad():out = inspect_module(x, **kwargs)if isinstance(out, tuple):out = out[0]return outelse:outs = []b_num = x.shape[0] // self._bsfor num in range(b_num):_x = x[num * self._bs:(num + 1) * self._bs]out = inspect_module(_x, **kwargs)if isinstance(out, tuple):out = out[0]outs.append(out)return torch.cat(outs, dim=0)

该方法用于前向传播。
如果输入的批量大小等于预设的批量大小，则直接进行前向传播。
否则，将输入按批量大小分割，分别进行前向传播，最后将结果拼接并返回。

`get_original_out`方法

@torch.no_grad()
def get_original_out(self, x, inspect_module, subset_kwargs):with torch.no_grad():org_out = self.inspect_module_forward(x, inspect_module, subset_kwargs)return org_out

该方法用于获取原始输出。
调用inspect_module_forward方法进行前向传播并返回结果。

`calculate_loss`方法

def calculate_loss(self, org_out, out):if out.shape[0] == self._bs:return (org_out - out).float().pow(2).mean().item()else:total_loss = 0.0b_num = org_out.shape[0] // self._bsfor num in range(b_num):_org_out = org_out[num * self._bs:(num + 1) * self._bs]_out = out[num * self._bs:(num + 1) * self._bs]single_loss = (_org_out - _out).float().pow(2).mean().item()total_loss += single_lossreturn total_loss / b_num

该方法用于计算损失。
如果输出的批量大小等于预设的批量大小，则直接计算均方误差。
否则，将输出按批量大小分割，分别计算每个批量的均方误差，最后求平均并返回。

`fake_quantize_weight`方法

def fake_quantize_weight(self, fc, scales, is_gqa, layer_name):if fc.weight.data.dtype == torch.float8_e4m3fn:tmp_weight_data = weight_cast_to_bf16(fc.weight.data,fc.weight_scale_inv.data).to(torch.bfloat16)else:tmp_weight_data = fc.weight.datatmp_weight_data = self.scaling_weight(tmp_weight_data, scales, is_gqa)tmp_weight_data = get_wquantizer(self.block_idx,layer_name,self.mix_bits_map,self.quantizer_mix_bits,self.wquantizer,).fake_quant_weight_dynamic(tmp_weight_data)if fc.weight.data.dtype == torch.float8_e4m3fn:fc.weight.data, fc.weight_scale_inv.data = weight_cast_to_fp8(tmp_weight_data)else:fc.weight.data = tmp_weight_datareturn fc.weight

该方法用于对权重进行伪量化。
根据权重的数据类型进行处理，调用scaling_weight方法对权重进行缩放。
调用get_wquantizer获取权重量化器，并对权重进行动态伪量化。
最后将伪量化后的权重赋值给原始权重并返回。

`fake_quantize_input`方法

def fake_quantize_input(self, x_tmp, layers_dict):if self._bs == x_tmp.shape[0]:x_tmp = get_aquantizer(self.block_idx,list(layers_dict.keys())[0],self.mix_bits_map,self.quantizer_mix_bits,self.aquantizer,).fake_quant_act_dynamic(x_tmp)else:outs = []for i in range(x_tmp.shape[0]):_x = x_tmp[i]_x = get_aquantizer(self.block_idx,list(layers_dict.keys())[0],self.mix_bits_map,self.quantizer_mix_bits,self.aquantizer,).fake_quant_act_dynamic(_x)outs.append(_x)x_tmp = torch.stack(outs)return x_tmp

该方法用于对输入进行伪量化。
如果输入的批量大小等于预设的批量大小，则直接调用激活值量化器对输入进行动态伪量化。
否则，将输入按样本分割，分别进行动态伪量化，最后将结果拼接并返回。

`search_scale_subset`方法

@torch.no_grad()
def search_scale_subset(self,prev_op,layers_dict,input,inspect_module,is_gqa,subset_kwargs
):if self.awq_bs is None:self._bs = input[0].shape[0]else:self._bs = self.awq_bsw_max = self.get_weight_scale(layers_dict)# grid search for ratiobest_error = float('inf')best_scales = Nonen_grid = 20org_sd = {k: v.cpu() for k, v in inspect_module.state_dict().items()}org_out_dict = {}for n in range(n_grid):loss_mean = 0scales_mean = 0for i in range(len(input)):input[i] = input[i].to(next(inspect_module.parameters()).device)x = input[i]if isinstance(subset_kwargs, list):kwargs = subset_kwargs[i]else:kwargs = subset_kwargsif i in org_out_dict:org_out = org_out_dict[i]else:org_out = self.get_original_out(x, inspect_module, kwargs)org_out_dict[i] = org_outratio = n * 1 / n_gridscales = self.get_scales(prev_op, x, w_max, is_gqa, ratio)for layer_name in layers_dict:fc = layers_dict[layer_name]fc.weight = self.fake_quantize_weight(fc, scales, is_gqa, layer_name)x_tmp = self.scaling_input(x, scales, is_gqa)if not check_w_only(self.block_idx,list(layers_dict.keys())[0],self.mix_bits_map,self.quantizer_mix_bits,self.w_only,):x_tmp = self.fake_quantize_input(x_tmp, layers_dict)out = self.inspect_module_forward(x_tmp, inspect_module, kwargs)if self.padding_mask and org_out.shape[1] == self.padding_mask[i].shape[-1]:org_out = org_out * self.padding_mask[i].unsqueeze(dim=-1).to(org_out.device)  # noqaout = out * self.padding_mask[i].unsqueeze(dim=-1).to(out.device)loss = self.calculate_loss(org_out, out)if len(input) == 1:n_samples = x.shape[0]else:n_samples = self.n_samplesloss_mean += x.shape[0] * 1.0 / n_samples * lossscales_mean += x.shape[0] * 1.0 / n_samples * scalesinspect_module.load_state_dict(org_sd)is_best = loss_mean < best_errorif is_best:best_error = loss_meanbest_scales = scales_meanif self.save_mem:del org_outdel outgc.collect()torch.cuda.empty_cache()# Synchronize across ranksbest_error_tensor = torch.tensor([best_error], device='cuda')dist.all_reduce(best_error_tensor, op=dist.ReduceOp.MIN)global_best_error = best_error_tensor.item()# Identify the rank with the minimum lossglobal_best_rank = torch.tensor([dist.get_rank()if abs(best_error - global_best_error) < 1e-5else -1],device='cuda')dist.all_reduce(global_best_rank, op=dist.ReduceOp.MAX)global_best_rank = global_best_rank.item()# Broadcast the best scales from the rank with the minimum loss to all ranksif dist.get_rank() == global_best_rank:dist.broadcast(best_scales, src=global_best_rank)else:best_scales = torch.zeros_like(best_scales, device='cuda')dist.broadcast(best_scales, src=global_best_rank)del org_out_dictgc.collect()torch.cuda.empty_cache()return best_scales

该方法用于搜索最佳的缩放因子。
首先设置批量大小，计算权重的最大缩放因子。
使用网格搜索的方法，遍历不同的比例值，计算每个比例下的缩放因子。
对权重和输入进行伪量化，计算损失。
选择损失最小的缩放因子作为最佳缩放因子。
在分布式训练中，同步不同进程的最佳损失和最佳缩放因子。
最后返回最佳缩放因子。

`block_transform`方法

@torch.no_grad()
def block_transform(self, block, input_feat, block_kwargs):if self.trans:super().block_transform(block, input_feat, block_kwargs)if self.weight_clip:logger.info('auto_clip start')logger.info(f'clip version: {self.clip_version}')self.auto_clipper.run(block,self.block_idx,input_feat,n_sample_token=self.config.calib.get('seq_len', None))logger.info('auto_clip finished')else:logger.info('disable weight clip')

该方法用于对块进行变换。
如果self.trans为True，则调用父类的block_transform方法。
如果self.weight_clip为True，则调用自动裁剪器对块进行裁剪。

`subset_transform`方法

@torch.no_grad()
def subset_transform(self,subset,input_feat,subset_kwargs,
):layers_dict = subset['layers']prev_op = subset['prev_op']input_name = subset['input'][0]inspect_module = subset['inspect']do_trans = subset.get('do_trans', True)if not do_trans:logger.info('do_trans is set to False. Do not transform this subset.')returnif not check_do_quant(self.block_idx,list(layers_dict.keys())[0],self.mix_bits_map,self.quantizer_mix_bits,):logger.info('This subset is set to float. No need to transform this subset.')returnif self.config['model']['type'] == 'Starcoder':if isinstance(prev_op[0], (nn.Linear, FakeQuantLinear)):logger.info('Do not transform this subset.')returnassert (len(prev_op) in (0, 1)), 'Only support single prev_op. If multi prev_ops, code need to be updated.'if len(prev_op) == 0 or (len(prev_op) == 1 and prev_op[0] is None):logger.info('Cannot apply scale. Do not transform this subset.')returnif isinstance(prev_op[0],tuple(_LLMC_LN_TYPES_ +_TRANSFORMERS_LN_TYPES_ +_LLMC_LINEAR_TYPES_ +_TRANSFORMERS_LINEAR_TYPES_),):layers = list(layers_dict.values())if (isinstance(prev_op[0], (nn.Linear, FakeQuantLinear))and prev_op[0].out_features != layers[0].in_features * 3and prev_op[0].out_features != layers[0].in_features * 2and prev_op[0].out_features != layers[0].in_features):if self.has_gqa and self.do_gqa_trans:is_gqa = Trueinput_keys = list(input_feat.keys())input_name = input_keys[input_keys.index(input_name) - 1]else:logger.info('Cannot apply scale. Do not transform this subset.')returnelse:is_gqa = Falsescale = self.search_scale_subset(prev_op[0],layers_dict,input_feat[input_name],inspect_module,is_gqa,subset_kwargs)self.apply_scale(scale, prev_op, layers)self.update_input_feat(scale, input_feat, layers_dict, is_gqa)if self.save_scale:for n in layers_dict:layer_name = f'{self.model.block_name_prefix}.{self.block_idx}.{n}'self.act_scales[layer_name] = scaleelse:logger.info('Do not transform this subset.')