论文导读 | 区间数据管理
1 问题背景
在很多应用场景下需要处理和管理区间数据(interval data)。一个区间由其起点 s t a r t start start 和终点 e n d end end 表示: [ s t a r t , e n d ] [start, end] [start,end] (需要 s t a r t ≤ e n d start \leq end start≤end)。例如在时序数据库(temporal database)中,每条记录(tuple)除了记录其原有信息,还额外存储了其有效期(valid time),其有效期就可以用一个区间的集合表示。再例如有时为了保护隐私,也可以用区间来代替具体的数值。下面的介绍中,统一采用时序数据库场景,每个区间代表了一条元组的有效期。
对于区间数据,有两类常见的查询类型:
- 范围查询(range queries)。给定一个查询区间 q = [ s , t ] q = [s, t] q=[s,t],返回数据库中有效期与 q q q 有交集的元组,即 R ( q ) = { e ∣ e ∈ A , e ∩ q ≠ ∅ } R(q)=\{e\mid e\in A, e\cap q\neq\emptyset\} R(q)={e∣e∈A,e∩q=∅}。例如,查找上个星期花粉过敏的同学,便是限定了时间范围为上周。点查询可以被视为特殊的范围查询,即起点等于终点。
- 持续时间查询(duration queries)。给定一个持续时间的阈值 d d d,查找数据库中有效期跨度不低于 d d d 的元组,即 R ( q ) = { e ∣ e ∈ A , ∣ e ∣ ≥ d } R(q)=\{e\mid e\in A, |e|\geq d\} R(q)={e∣e∈A,∣e∣≥d}。例如,查询上个星期工作超过 40 小时的员工,这里持续时间阈值被设定为 40 小时。
任给两个区间 [ a , b ] [a, b] [a,b] 和 [ s , t ] [s, t] [s,t],它们要么相交(overlap, intersect),要么不相交(disjoint),如下图所示。其中 3 和 4 代表了一种特殊的相交关系——包含。很容易发现,两个区间相交的条件为 max ( a , s ) ≤ min ( b , t ) \max(a, s)\leq \min(b,t) max(a,s)≤min(b,t),且交集为 [ max ( a , s ) , min ( b , t ) ] [\max(a,s), \min(b,t)] [max(a,s),min(b,t)]。

最简单管理区间的办法为直接存储这些区间数据,查询时读取这些区间,一条条地处理。这种方法会引起较高的运行时代价。还可以采用位数组(bitset)表示区间,两个位数组与运算结果非零,就意味着两个区间有交。但位数组方法的存储开销较大,因为每条记录需要全体时间范围的存储代价。因此,最近的研究主要集中在两方面:(1)更快的在线处理算法;(2)更高效的索引以及配套算法。
2 区间集合求交方法
给定两个区间集合 R R R 和 S S S,他们的区间交集结果被定义为 R ⋈ S = { ( r , s ) ∣ r ∈ R , s ∈ S , r ∩ s ≠ ∅ } R\bowtie S=\{(r,s)\mid r\in R, s\in S, r\cap s\neq\emptyset\} R⋈S={(r,s)∣r∈R,s∈S,r∩s=∅}。这种定义是合理的,因为有时候并不需要知道 r r r 与 s s s 的交区间具体是多少,而是仅需知道它们有交;并且,若已知 r r r 与 s s s 有交,可以通过 O ( 1 ) O(1) O(1) 的时间,求出具体的交区间。
现有的区间集合求交方法可以被分为两类:(1)基于扫描线的方法;(2)归并连接方法。
2.1 Endpoint-based Interval Join (EBI 1 ^1 1)
一个区间集合 R R R 也可被视作事件集合: { ( e n d p o i n t , t y p e , i d ) ∣ t y p e ∈ { s t a r t , e n d } } \{(endpoint, type, id)\mid type\in\{start, end\}\} {(endpoint,type,id)∣type∈{start,end}},其中 endpoint 为每个区间的起点和终点,故共有 2 ∣ R ∣ 2|R| 2∣R∣ 条事件。EBI 中将需要求交的两个区间集合 R R R 和 S S S 的事件集合按照 endpoint 和 type 排序。求交过程中,按照 endpoint 从小到大依次扫描事件,并维护当前 R R R 和 S S S 中已经开始、还没有结束的区间 A R A^R AR 和 A S A^S AS(称为活跃集合)。每次扫描到一条 start 事件,就说明其与另一个集合中的活跃集合都有交集,将这些交集加入结果 J J J 中;若扫描到一条 end 事件,则从活跃集合中删去改区间。具体算法流程如下.

2.2 Forward Scan Interval Join (FS 2 ^2 2)
FS 方法直接处理区间,预处理时按照每个区间的起点进行排序。求交时,并不像 EBI 一样维护活跃集合,而是运行时通过对于另一个集合中的区间进行前向扫描,检查哪些区间可以与当前区间有交,并更新结果。具体算法如下所示。

2.3 FS with Grouping and Bucket Indexing (gbFS 3 ^3 3)
注意到 EBI 和 FS 分别需要做 2 ( ∣ R ∣ + ∣ S ∣ ) 2(|R|+|S|) 2(∣R∣+∣S∣) 和 ( ∣ R ∣ + ∣ S ∣ + ∣ R ⋈ S ∣ ) (|R|+|S|+|R\bowtie S|) (∣R∣+∣S∣+∣R⋈S∣) 次端点比较,如果能减少 FS 方法中产生结果过程中的比较次数 ∣ R ⋈ S ∣ |R\bowtie S| ∣R⋈S∣,便会提高求交算法的性能。gbFS 中提出了两个针对 FS 的优化技巧,实现减少比较次数。
第一个优化是分组,当 r . s t a r t < s . s t a r t r.start < s.start r.start<s.start 时,找到 R R R 中 r r r 之后的所有 $ r’:r’.start<s.start$,与 r r r 一起形成了一个分组 G R G^R GR。分组的好处时,当 s s s 与 r r r 有交时,那 s s s 也一定与 r ′ r' r′ 有交。便可不经过比较而之间产生结果。
第二个优化时分桶索引,将区间的全集分为几个小片段,每个片段上存储那些开始于该片段的区间。对于一个跨越多个片段的区间 r r r 来说, S S S 中起始于非两端片段的那些区间一定与 r r r 有交。
下图展示了这两个优化的具体例子,gFS 为仅采用分组优化的方法,gbFS 为同时采用两种优化的方法。图中灰色区域为分桶优化中无需比较的区域,阴影部分为每种方法需要进行比较的区域。

最后 bgFS 还采用了并行技术加速求交,具体可以参看原文。
下图展示了在两个真实数据集上,FS、gFS 和 gbFS 区间集合求交的性能比较。可以发现运行速度确实随着比较次数的降低而加快。在 BOOKS 数据集上分组优化效果明显,这是因为该数据集中跨度大的区间数量多,因此一个分组内的区间数量较多,能充分利用分组。

2.4 Disjoin Interval Partitioning (DIP 4 ^4 4)
若采用类似关系型数据中的归并连接方法,不可避免需要做回溯(backtracking),带来过多的比较次数。若提前对区间集合进行划分,使得每个划分内,区间都是不交的,则可在求交中避免回溯,从有结果的最后一个区间开始,减少比较次数。如下图所示,通过对 R R R 和 S S S 划分,将比较次数从 29 减小到 21。
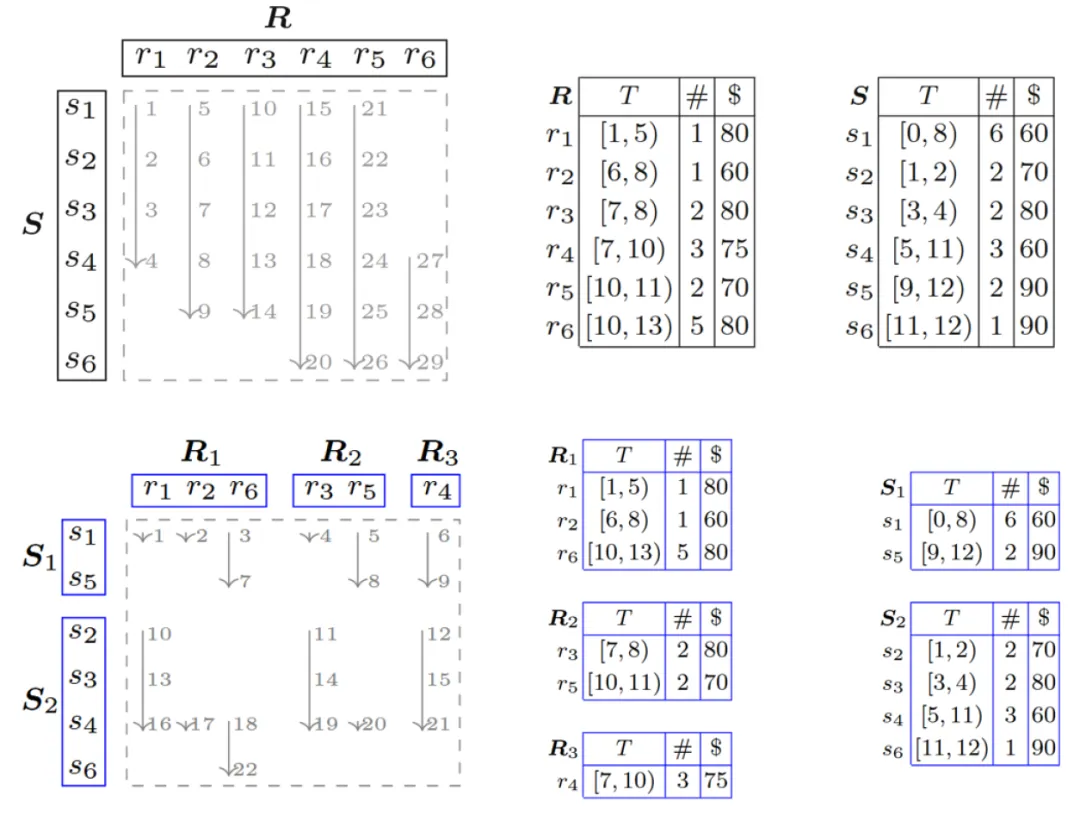
区间的不交划分可以通过贪心算法得到:按照区间起点和终点从小到大的次序遍历所有区间,遍历过程中维护一个最小堆,记录每个划分的终止时间。若当前区间的起始时间大于堆顶时间,则可将该区间加入堆顶元素对应的划分;否则需要新增一个划分存储该区间。
3 范围查询方法
区间数据的范围查询方法都维护了一些索引。这些索引或根据时间点,或根据时间片段,将数据库中的区间数据分配到一些分片上作为索引。查询时便可通过索引快速定位相关区间,避免全遍历的高开销。
3.1 Interval Tree 5 ^5 5
采用区间树结构存储区间数据时,需要选取一些时间点,构成二叉搜索树。插入区间时,从树根出发,若该区间包含对应节点的时间点,则将区间存储在对应节点。否则存储到节点的对应后代节点。查询时,若查询区间包含区间数节点代表的时间点,则该节点存储的的所有区间都将被返回;再接着查看左右孩子是否有与查询区间相交的结果。

3.2 Timeline Index 6 ^6 6
数据库中常用快照方式进行事务管理。Timeline Index 也采用这种思想,选取若干时间点建立快照,快照中存储对应时间点上还活跃的区间。这样在查询时,从查询区间的起始时间之前,寻找到最近的快照,做一次扫描便可恢复出查询区间上活跃的区间。

3.3 1D Grid 7 ^7 7
1D Grid 将区间全集划分为若干片段,每个片段上存储与该片段有交的区间(因此一个区间可能在多个片段都被存储)。查询时,将查询区间和查询区间对应的片段中的区间比较,即可得到结果。这里需要注意两点:(1)结果是需要去重的,例如下图中的 s 4 s_4 s4 在 P 2 P_2 P2 和 P 3 P_3 P3 中都与 q q q 有交,可以采用 Reference value 方法[^7]进行去重;(2)对查询区间对应的片段,无需进行比较,直接返回结果,例如下图中 q q q 跨越了三个片段,而中间片段 P 3 P_3 P3 中存储的区间一定与 q q q 有交,可以直接返回为结果。
3.4 Period Index 8 ^8 8
Period Index 被用在 Range duration 查询中,即需要返回在某个时间范围内,区间跨度也在一定范围内的区间数据。下图展示了 Period Index 的一个示例,不同层次(level)存储了区间跨度在不同范围内的区间,每个区间最多在同一个跨度的两个片段中出现。蓝色区域为对于查询:(1)时间范围为 KaTeX parse error: Undefined control sequence: \mbox at position 3: [4\̲m̲b̲o̲x̲{-}Aug\mbox{-}2…;(2)持续时间范围为 [ 5 h , 10 h ] [5h, 10h] [5h,10h] 需要查找的片段。Period Index 也可以用于范围查询,只需查找对应时间范围内的片段即可。

Overlap Interval Partition Join (OIP 9 ^9 9)
OIP 中首先将区间全集划分为等长的若干片段,将起点在 i i i 、终点 在 j j j 片段的区间存储在 P i , j P_{i,j} Pi,j 中,并将所有 P i , j P_{i,j} Pi,j 组织成链状形式(下图左下(a)),查询时从最大的区域开始,从左至右、从上至下地探查。为了避免某些区域内没有区间数据,OIP 还应用了惰性方法,仅组织有数据的 P i , j P_{i,j} Pi,j(下图右下(b))。

3.5 Hierarchical Index for Intervals (HINT 10)
与前面方法不同,HINT为每个区域存储的区间为完全包含该区域的区间。如下图上部中,区间 [ 5 , 9 ] [5, 9] [5,9] 将在蓝色线段对应的三个区域 P 4 , 5 P_{4, 5} P4,5, P 3 , 3 P_{3,3} P3,3 和 P 3 , 4 P_{3, 4} P3,4 中存储。查询时只需要从包含查询区间的区域内读取数据即可,无需进一步检查。如查找与 [ 5 , 9 ] [5, 9] [5,9] 有交的区间数据,即可从下图下部的蓝色和红色线段对应的区域读取包含这些区域的区间。HINT 需要去重,去重可以通过对于每个区域数据进一步分为两部分:(1)起始于该区域;(2)在该区域之前起始。由此,每层的非首区域仅需读取从起始于该区域的区间即可。下图下部中,仅对于蓝色线段需要读取全部数据;而对于红色部分仅需读取起始于这些区域的区间。

4 结论
现有的区间数据索引可以分为两类:
(1)划分后每个区域存储与该区域有交的区间;(2)划分后每个区域存储完全包含该区域的区间。具体使用时,需要根据不同应用场景选择合适的索引方法,例如,如果用来做过滤,可采用(1)中的方法,因为每个与查询区间无交的区域中的数据一定与查询区间无交;而 HINT 这种第(2)类方法,处理范围查询更块,因为区域内的数据无需比较便可被返回。
参考文献
[1]: An interval join optimized for modern hardware. 2016. ICDE. Danila Piatov, Sven Helmer, Anton Dignös.
[2]: Efficient processing of spatial joins using R-trees. 1993. SIGMOD. Thomas Brinkhoff, Hans-Peter Kriegel, Bernhard Seeger.
[3]: A forward scan based plane sweep algorithm for parallel interval joins. 2017. VLDB. Panagiotis Bouros, Nikos Mamoulis.
[4]:Disjoint interval partitioning. 2017. VLDBJ. Francesco Cafagna, Michael H. Böhlen.
[5]: Dynamic Rectangle Intersection Searching. Technical Report 47. 1980. Herbert Edelsbrunner.
[6]: Timeline index: a unified data structure for processing queries on temporal data in SAP HANA. 2013. SIGMOD. Martin Kaufmann, Amin Amiri Manjili, Panagiotis Vagenas, Peter M. Fischer, Donald Kossmann, Franz Färber, and Norman May.
[7]:Data Redundancy and Duplicate Detection in Spatial Join Processing. 2000. ICDE. Jens-Peter Dittrich and Bernhard Seeger.
[8]: Period Index: A Learned 2D Hash Index for Range and Duration Queries. 2019. SSTD. Andreas Behrend, Anton Dignös, Johann Gamper, Philip Schmiegelt, Hannes Voigt, Matthias Rottmann, and Karsten Kahl.
[9]: Overlap interval partition join. 2014. SIGMOD. Anton Dignös, Michael H. Böhlen, Johann Gamper.
[10]:HINT: A Hierarchical Index for Intervals in Main Memory. 2022. SIGMOD. George Christodoulou, Panagiotis Bouros, Nikos Mamoulis
