统计随机行走的结构占比

有一个点在平面上移动，设r1，r2是0到1的两个随机数，这个点单次移动的距离是5*r1，移动的角度是360*r2，取整，走1万步，将相邻的4点放到一起，统计4点结构占比。

如某次随机得到10个点

1		2	2
2		2	2
3		2	4
4		2	5
5		2	3
6		4	4
7		4	4
8		5	4
9		2	2
10		0	3

	0	1	2	3	4	5
0				10
1
2			1--2--9	5	3	4
3
4					6--7
5					8

其中1，2，9是重复的，6，7是重复的。所以1，2，3，4这个组合只有3个点，第一个合理的组合是2，3，4，5

	0	1	2	3	4	5				0	1	2	3	4	5				0	1	2	3	4	5
0									0									0				10
1									1									1
2			2	5	3	4			2				5	3	4			2			9
3									3									3
4									4					6				4					7
5									5									5					8

只有3个合理的组合2，3，4，5；3，4，5，6和7，8，9，10分别是16，4，7.

随机1万次得到16个结构占比为

1	2	3	4	5	6	7	8	9	10
215	934	265	284	234	58	563	109	615	250
11	12	13	14	15	16
266	34	227	204	132	47

再随机1万次，统计相邻5点的结构占比，得到

1	2	3	4	5	6	7	8	9	10
76	126	79	93	215	360	205	60	138	56
11	12	13	14	15	16	17	18	19	20
41	20	164	74	22	99	47	166	39	89
21	22	23	24	25	26	27	28	29	30
114	227	44	13	2	39	43	140	76	117
31	32	33	34
83	44	50	8

由结构加法，将5压缩为4

7(4a1+1)=2*5a1+5a2+5a3+5a4+2*5a12

24(4a2+1)=2*5a2+2*5a3+2*5a4+2*5a5+2*5a6+2*5a7+2*5a9+2*5a13+2*5a14+4*5a15+2*5a21

11(4a3+1)=5a1+5a7+2*5a8+3*5a10+2*5a12+2*5a14

11(4a4+1)=2*5a3+5a5+2*5a8+3*5a11+2*5a24+5a29

13(4a5+1)=5a1+5a7+5a10+2*5a17+4*5a19+2*5a20+2*5a27

7(4a6+1)=5a10+5a19+5*5a25

17(4a7+1)=2*5a2+5a6+5a7+5a9+3*5a20+2*5a22+3*5a28+4*5a31

6(4a8+1)=5a1+5a9+3*5a27+5a31

17(4a9+1)=5a5+5a6+5a13+3*5a16+3*5a18+2*5a21+2*5a22+4*5a30

13(4a10+1)=5a5+5a11+2*5a16+4*5a23+2*5a26+5a29+2*5a32

11(4a11+1)=5a4+5a8+5a9+5a13+3*5a17+5a22+3*5a26

3(4a12+1)=5a12+5a15+5a24

10(4a13+1)=5a6+2*5a18+2*5a28+5*5a33

7(4a14+1)=5a4+5a14+5a21+2*5a24+2*5a29

6(4a15+1)=5a13+5a29+5a30+3*5a32

7(4a16+1)=5a11+5a23+5*5a34

如4a1=(2*76+126+79+93+2*20)/7=70，得到

1	2	3	4	5	6	7	8	9	10
70	134.3	68.82	65.27	65.46	15	142.8	71	157.9	67.08
11	12	13	14	15	16
85.45	18.33	122.2	65.57	81.5	17.86

两组数据归一化

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
0.048	0.211	0.06	0.064	0.053	0.013	0.127	0.025	0.139	0.056	0.06	0.008	0.051	0.046	0.03	0.011
0.056	0.108	0.055	0.052	0.052	0.012	0.114	0.057	0.127	0.054	0.068	0.015	0.098	0.053	0.065	0.014

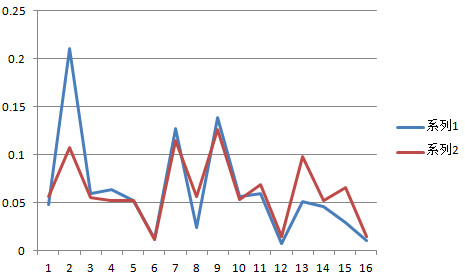
两条曲线很一致，但又不完全重合，这个点的长期行为和短期行为有内在的一致性，但又不完全一致。

按现有计算用n+1计算n，n越大两条曲线符合程度越好。这个过程或许可以理解为用离散运动逼近连续运动，n越大，点数越多曲线越平滑。