《Pytorch深度学习实践》ch2-梯度下降算法
------B站《刘二大人》
1.Gradient Decent
- 局部最优,全局最优,非凸函数:

- 梯度下降算法公式:

2.Implementation
import matplotlib.pyplot as plt# 数据集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]# 权重
w = 1.0# 模型
def forward(x): return x * w# 损失函数
def cost(xs, ys):cost = 0for x, y in zip(xs, ys):y_pred = forward(x)cost += (y_pred - y) ** 2return cost / len(xs) # 梯度下降
def gradient(xs, ys):grad = 0for x, y in zip(xs, ys):y_pred = forward(x)grad += 2 * x * (y_pred - y)return grad / len(xs)# 训练轮数 epoch 为横坐标,损失 Cost 为纵坐标
epoch_list = []
cost_list = []print('Predict (before training)', 4, forward(4))for epoch in range(100):cost_val = cost(x_data , y_data)grad_val = gradient(x_data,y_data)w -= 0.01 * grad_val # 0.01 为学习率epoch_list.append(epoch)cost_list.append(cost_val)print('Epoch:', epoch, 'w=', w, 'cost=', cost_val)print('Predict (after training)', 4, forward(4))# 绘图
plt.plot(epoch_list, cost_list)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.grid()
plt.show- 迭代如下:

- 绘制图形如下:

3.Discussion
- 如何让曲线变得更平滑:“加权”;
- 如果曲线最终没有趋于收敛:常见原因是 a 太大 ;

4. Stochastic Gradient Decent
- 相比于GD,SGD(随机梯度下降):每次随机选择一个样本,优势在于有可能跨过局部最优,并且曲线也更加平滑;

- 代码修改如下:
import matplotlib.pyplot as plt# 数据集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]# 权重
w = 1.0# 模型
def forward(x): return x * w# 损失函数
def loss(x, y):y_pred = forward(x)return (y_pred - y) * (y_pred - y)# 梯度下降
def gradient(x, y):y_pred = forward(x)return 2 * x * (y_pred - y)# 训练轮数 epoch 为横坐标,损失 loss 为纵坐标
epoch_list = []
loss_list = []print('Predict (before training)', 4, forward(4))for epoch in range(100):for x, y in zip(x_data, y_data):loss_val = loss(x , y)grad_val = gradient(x,y)w -= 0.01 * grad_val # 0.01 为学习率epoch_list.append(epoch)loss_list.append(loss_val)print('Epoch:', epoch, 'w=', w, 'loss=', loss_val)print('Predict (after training)', 4, forward(4))# 绘图
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.grid()
plt.show- 迭代如下:

- 绘制图形如下:

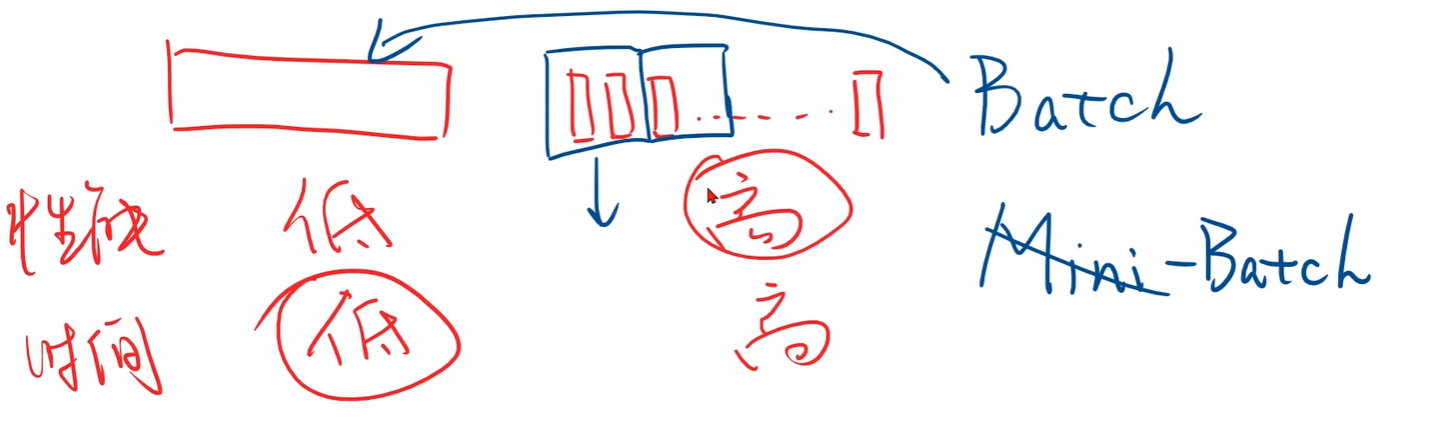
5.Comparison
- 随机梯度算法虽然性能更好,但是时间复杂度高,于是取折中:Batch;