【DSP笔记】解锁频率之秘：Z 变换与离散傅里叶变换的深度探索

解锁频率之秘：Z 变换与离散傅里叶变换的深度探索

想象一下，你是一位经验丰富的机械师，面对一台复杂的机器。时域分析就像你拿着放大镜，仔细观察每一个齿轮的转动，每一个连杆的摆动，这些细节无疑很重要，但整体的协调性、机器的“韵律”可能难以一眼看出。而频率域分析，就像你戴上特制的眼镜，瞬间就能看到机器的“心跳”，哪些部件在高速振动，哪些在低速运转，甚至能察觉到机器发出的“不和谐音”。

DTFT 和 Z 变换，就是这样的“特制眼镜”，它们帮助我们从信号的“形态”转变为信号的“成分”或“特征”，从而更高效地分析和设计系统。

探索信号的“频率成分”：离散时间傅里叶变换 (DTFT)

傅里叶分析的核心思想是，任何一个复杂的信号，都可以被分解成一系列简单的正弦（或复指数）信号的叠加。DTFT就是将这个思想应用到离散时间信号上。

DTFT 的“魔法公式”

对于一个离散时间序列 $x(n)$，它的离散时间傅里叶变换 (DTFT) 定义为：
$$X(e^{j\omega })=\sum _{n=-\infty }^{\infty }x(n)e^{-j\omega n}$$
其中：

• $X(e^{j\omega })$ 是信号的频率响应，一个关于数字角频率 $\omega$ 的连续函数。注意，这里的 $e^{j\omega }$ 表示 $z$ 平面单位圆上的点，这是DTFT与Z变换的天然联系。
• $\omega$ 是数字角频率，取值范围通常为 $[-\pi ,\pi )$ 或 $[0,2\pi )$。
• $e^{-j\omega n}$ 类似于模拟傅里叶变换中的复指数项，代表了不同频率的“探针”。

反过来，如果我们知道了信号的DTFT $X(e^{j\omega })$，我们可以通过逆离散时间傅里叶变换 (IDTFT) 恢复原始序列 $x(n)$：
$$x(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\omega })e^{j\omega n}d\omega$$
这就像我们把一个复杂的乐章分解成了各种音符的组合，又可以把这些音符重新组合成原来的乐章。

DTFT 的核心特性：简化计算的“秘密武器”

DTFT之所以强大，在于它拥有一系列优良的性质，这些性质能极大地简化信号处理的分析和计算。

1. 周期性： $X(e^{j\omega })$ 是关于 $\omega$ 的周期函数，周期为 $2\pi$。这意味着我们只需要分析一个 $2\pi$ 的周期内的频谱就足够了。

2. 线性： 如果 $x_1(n)\leftrightarrow X_1(e^{j\omega })$ 且 $x_2(n)\leftrightarrow X_2(e^{j\omega })$，那么 $a{x}_1(n)+b{x}_2(n)\leftrightarrow a{X}_1(e^{j\omega })+b{X}_2(e^{j\omega })$。

3. 时移特性： $x(n-n_0)\leftrightarrow e^{-j\omega n_0}X(e^{j\omega })$。
   信号在时域的延迟，对应于频域的相位改变（乘以一个复指数）。这个性质在通信系统中的延时补偿、滤波器设计中非常有用。

4. 频移特性： $e^{j{\omega }_{0}n}x(n)\leftrightarrow X(e^{j(\omega -{\omega }_0)})$。
   信号在时域乘以一个复指数（相当于载波调制），对应于频域的频谱搬移。在通信系统中用于实现信号的上下变频。

5. 共轭对称性： 如果 $x(n)$ 是实序列，那么其DTFT的幅度谱是偶对称的 ($|X(e^{j\omega })|=|X(e^{-j\omega })|$)，相位谱是奇对称的 ($\angle X(e^{j\omega })=-\angle X(e^{-j\omega })-2\pi k$)。
   这个性质在设计实数滤波器时非常有用，可以减少计算量。

6. 时域卷积定理： 这是DTFT最重要的性质之一！
   $$y(n)=x(n)\ast h(n)\leftrightarrow Y(e^{j\omega })=X(e^{j\omega })H(e^{j\omega })$$
   这意味着，在时域复杂的卷积运算，在频域变成了简单的乘法运算！这对于LTI系统的分析和设计来说，简直是革命性的。它让我们可以直接在频率域设计滤波器，通过修改 $H(e^{j\omega })$ 来实现对特定频率成分的增强或衰减。

7. Parseval 定理： 信号的能量在时域和频域是守恒的。
   $$\sum _{n=-\infty }^{\infty }|x(n){|}^2=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }|X(e^{j\omega }){|}^{2}d\omega$$
   它为我们提供了一种衡量信号能量的另一种方式。

离散傅里叶级数 (DFS)：周期序列的频谱

对于周期序列 $\tilde{x}(n)$（周期为 $N$），我们不能直接使用DTFT，因为周期信号的能量是无限的，DTFT会得到冲激函数。我们使用离散傅里叶级数 (DFS) 来表示它们。

• 定义：
  $$\tilde{X}(k)=\sum _{n=0}^{N-1}\tilde{x}(n)W_N^{kn},k=0,1,\dots ,N-1$$
  $$\tilde{x}(n)=\frac{1}{N}\sum _{k=0}^{N-1}\tilde{X}(k)W_N^{-kn},n=0,1,\dots ,N-1$$
  其中 $W_N=e^{-j2\pi /N}$。

• 与DTFT的关系： 周期序列的DTFT是一个冲激串，冲激的位置在 $2\pi k/N$，强度与DFS系数相关。

摆脱“收敛”的束缚：Z 变换的强大通用性

DTFT虽然强大，但它有一个局限性：不是所有序列的DTFT都收敛。例如，单位阶跃序列 $u(n)$ 就没有收敛的DTFT。为了解决这个问题，我们引入了更通用的Z 变换。

Z 变换的定义：DTFT 的推广

Z 变换可以看作是DTFT的推广。它引入了一个复变量 $z$，不再限制在单位圆上。
对于一个离散时间序列 $x(n)$，它的 Z 变换定义为：
$$X(z)=\sum _{n=-\infty }^{\infty }x(n)z^{-n}$$
其中 $z$ 是一个复数，通常表示为 $z=r{e}^{j\omega }$。

• 当 $|z|=r=1$ 时，$z=e^{j\omega }$，Z 变换就退化为DTFT。
• Z 变换的存在要求无穷级数 ${\sum }_{n=-\infty }^{\infty }x(n)z^{-n}$ 能够收敛。

收敛域 (Region of Convergence, ROC)：Z 变换的“身份证”

ROC是Z变换中最最重要的概念之一！它定义了Z变换存在的 $z$ 值区域。如果一个序列的Z变换存在，那么它就有一个特定的ROC。

为什么ROC如此重要？
因为不同的序列可能有相同的Z变换表达式，但它们的ROC不同，意味着它们代表了完全不同的时域序列。离开了ROC，Z变换就没有意义！ ROC就像Z变换的“身份证”，标识着它是哪个序列的Z变换。

序列类型对ROC的影响：

1. 有限长序列：

   • 序列只在有限个 $n$ 值上有非零值。
   • ROC是整个 $z$ 平面（可能不包含 $z=0$ 或 $z=\infty$，取决于序列是否在这些点有值）。
   • 例如：$\delta (n)$ 的 Z 变换是 $1$，ROC 是整个 $z$ 平面。

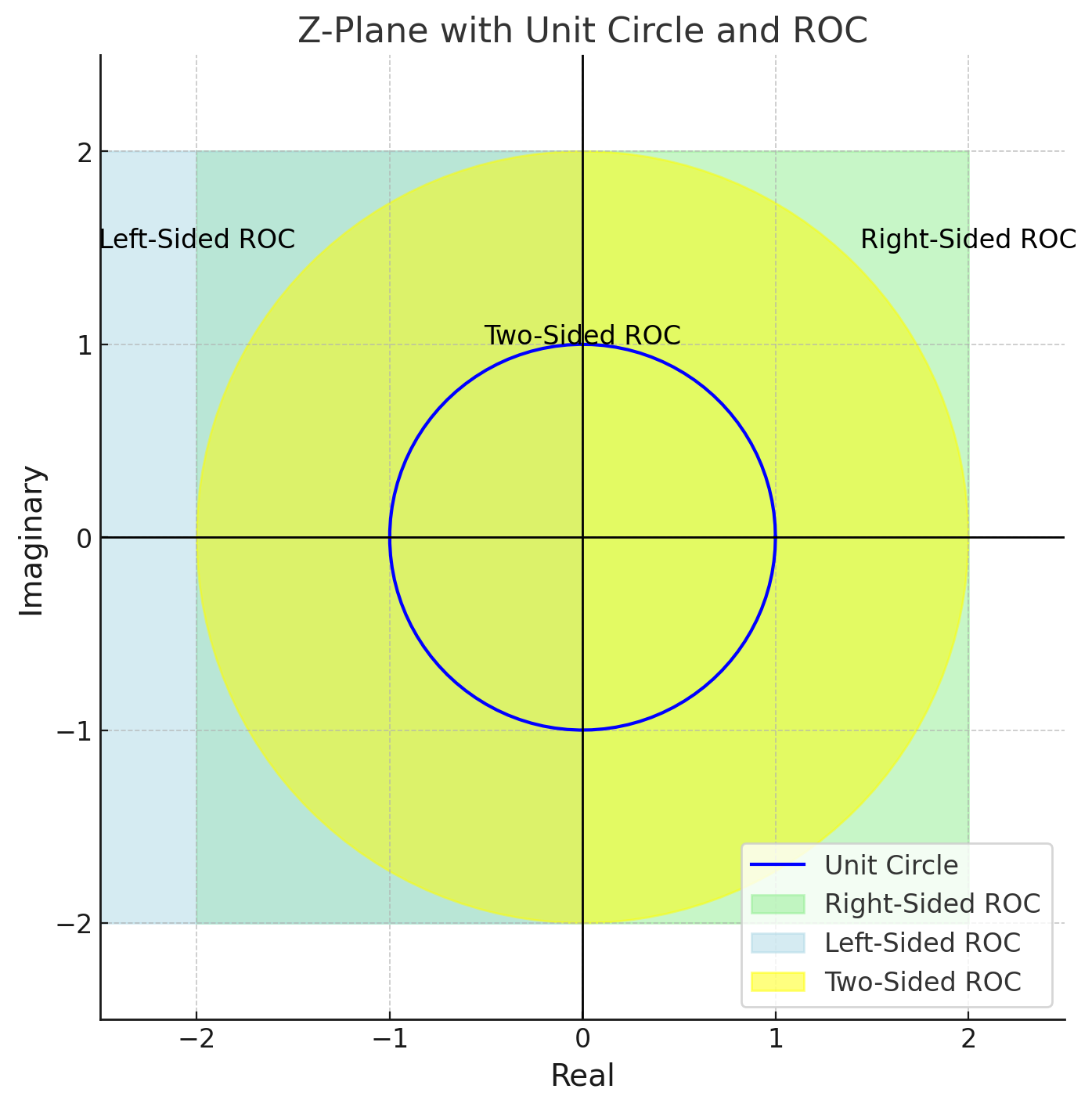
2. 右边序列 (Right-Sided Sequence)：

   • 序列只在 $n\ge N_1$（某个有限值）时有非零值。最常见的是因果序列（$N_1=0$）。
   • ROC是一个圆的外部区域，即 $|z|>r_0$。这个 $r_0$ 是由离原点最远的极点决定。
   • 例如：$a^{n}u(n)$ 的 Z 变换是 $\frac{1}{1-a{z}^{-1}}$，ROC 是 $|z|>|a|$。

3. 左边序列 (Left-Sided Sequence)：

   • 序列只在 $n\le N_2$（某个有限值）时有非零值。
   • ROC是一个圆的内部区域，即 $|z|<r_0$。这个 $r_0$ 是由离原点最近的极点决定。
   • 例如：$-a^{n}u(-n-1)$ 的 Z 变换也是 $\frac{1}{1-a{z}^{-1}}$，但ROC是 $|z|<|a|$。看，Z变换表达式相同，但ROC不同，代表的序列也就不同！

4. 双边序列 (Two-Sided Sequence)：

   • 序列在正负无穷都有非零值。
   • ROC是一个环形区域，即 $r_1<|z|<r_2$。
   • 例如：$x(n)=a^{n}u(n)+b^{n}u(-n-1)$ 的Z变换ROC可能是环形。

逆 Z 变换：从 Z 域回到时域

知道了序列的 Z 变换 $X(z)$ 和其 ROC，我们就可以通过逆 Z 变换 (IZT) 恢复原始序列 $x(n)$。

主要方法：

1. 部分分式展开法：

   • 这是最常用的方法。将 $X(z)$ (或 $X(z)/z$) 展开为若干个简单分式的和。
   • 对于每个简单分式，根据其形式和ROC，对照Z变换对表，就可以找到对应的时域序列。
   • 关键： 必须结合ROC来确定每个分式对应的序列是右边序列还是左边序列。

   步骤：

   1. 如果 $X(z)$ 是一个真分式（分子阶数小于分母阶数），则直接展开。如果不是，可以先除以 $z$ 得到 $X(z)/z$，展开后再乘以 $z$ 回去。
   2. 找到分母多项式的根（极点）。
   3. 进行部分分式展开。
   4. 根据 Z 变换对表和 ROC，确定每一项的逆 Z 变换。

2. 幂级数展开法：

   • 将 $X(z)$ 展开为关于 $z^{-1}$ 或 $z$ 的幂级数。
   • 级数展开的系数就是序列 $x(n)$ 的值。
   • 这种方法适用于有限长序列或需要求序列前几项值的情况。
   • 关键： 同样需要结合ROC来确定是按 $z^{-1}$ 展开（对应右边序列）还是按 $z$ 展开（对应左边序列）。

Z 变换的核心特性：LTI 系统分析的利器

Z 变换也拥有一系列重要的性质，这些性质使得它在LTI系统分析中发挥着关键作用。

1. 线性： 与DTFT类似，$a{x}_1(n)+b{x}_2(n)\leftrightarrow a{X}_1(z)+b{X}_2(z)$。
2. 时移特性： $x(n-n_0)\leftrightarrow z^{-n_0}X(z)$。
   这个性质在求解差分方程时至关重要，它将时域的延迟操作直接转换为Z域的乘法。
3. 乘以指数序列： $a^{n}x(n)\leftrightarrow X(z/a)$。
   这表明在时域乘以一个指数因子，在Z域会引起Z平面的尺度变换。
4. 微分特性： $nx(n)\leftrightarrow -z\frac{dX(z)}{dz}$。
   这个性质可以用来计算某些复杂序列的Z变换，或者证明其他性质。
5. 时域卷积定理： 这是Z变换最重要的性质之一！
   $$y(n)=x(n)\ast h(n)\leftrightarrow Y(z)=X(z)H(z)$$
   和DTFT一样，它把时域的卷积变成了Z域的简单乘法！这是Z变换能大大简化系统分析和设计的根本原因。

利用 Z 变换解差分方程：大招来了！

还记得第一章我们用递推法解差分方程吗？当序列较长时，那会非常麻烦。Z 变换提供了更优雅、更高效的解决方案！

利用Z变换解差分方程的步骤：

1. 对差分方程两边进行Z变换：

   • 利用 Z 变换的线性性质。
   • 利用 Z 变换的时移性质：$\mathrm{ZT}[y(n-k)]=z^{-k}Y(z)+{\sum }_{m=1}^{k}y(-m)z^{m-k}$ (这个是考虑非零初始条件的情况，如果初始条件为零，就简化为 $z^{-k}Y(z)$)。
   • 对于输入 $x(n)$ 也同样进行Z变换。

2. 代数求解 $Y(z)$：
   将Z变换后的方程视为一个代数方程，解出 $Y(z)$ 的表达式，通常是 $z$ 的有理分式。

3. 对 $Y(z)$ 进行逆Z变换：
   利用部分分式展开法（或幂级数展开法），将 $Y(z)$ 转换为时域输出序列 $y(n)$。在这一步，需要结合系统的因果性或稳定性来确定正确的ROC，从而选择正确的逆变换形式。

例子： 求解 $y(n)-0.5y(n-1)=x(n)$，已知 $x(n)=u(n)$，初始条件 $y(-1)=0$。

1. Z变换：
   $Y(z)-0.5(z^{-1}Y(z)+y(-1)z^0)=X(z)$
   $Y(z)-0.5z^{-1}Y(z)=X(z)$ (因为 $y(-1)=0$)
   $Y(z)(1-0.5z^{-1})=X(z)$
2. 求解 $Y(z)$：
   $X(z)=\frac{1}{1-z^{-1}}$ (对于 $u(n)$，ROC 是 $|z|>1$)
   $Y(z)=\frac{X(z)}{1-0.5z^{-1}}=\frac{1}{(1-z^{-1})(1-0.5z^{-1})}$
3. 逆Z变换：
   $Y(z)=\frac{A}{1-z^{-1}}+\frac{B}{1-0.5z^{-1}}$
   解得 $A=2,B=-1$ (具体计算略)。
   $Y(z)=\frac{2}{1-z^{-1}}-\frac{1}{1-0.5z^{-1}}$
   由于系统是因果的，其ROC应该包含输入 $u(n)$ 的ROC（$|z|>1$）以及系统本身的ROC（通常是所有极点外的区域）。在此例中，系统极点在 $z=1$ 和 $z=0.5$，所以系统的ROC是 $|z|>1$。
   因此，两项都对应右边序列：
   $y(n)=2u(n)-(0.5{)}^{n}u(n)$。

系统函数与频率响应：从 Z 域看系统特性

Z 变换不仅能解差分方程，它更是分析LTI系统特性（如因果性、稳定性、频率响应）的强大工具。

系统函数 $H(z)$：系统的“数学模型”

对于一个LTI系统，当初始条件为零时，其输出 $Y(z)$ 与输入 $X(z)$ 的 Z 变换之比，称为系统的系统函数 (System Function)，用 $H(z)$ 表示：
$$H(z)=\frac{Y(z)}{X(z)}$$
如果系统由线性常系数差分方程描述：${\sum }_{k=0}^N{a}_{k}y(n-k)={\sum }_{m=0}^M{b}_{m}x(n-m)$
对其进行Z变换（零初始条件）：${\sum }_{k=0}^N{a}_k{z}^{-k}Y(z)={\sum }_{m=0}^M{b}_m{z}^{-m}X(z)$
于是，系统函数为：
$$H(z)=\frac{{\sum }_{m=0}^M{b}_m{z}^{-m}}{{\sum }_{k=0}^N{a}_k{z}^{-k}}$$
系统函数 $H(z)$ 是 $z$ 的有理分式，可以表示为零点和极点的乘积形式：
$$H(z)=\frac{b_0}{a_0}\frac{{\prod }_{m=1}^M(1-c_m{z}^{-1})}{{\prod }_{k=1}^N(1-d_k{z}^{-1})}$$
其中 $c_m$ 是零点（使 $H(z)=0$ 的 $z$ 值），$d_k$ 是极点（使 $H(z)\to \infty$ 的 $z$ 值）。

频率响应函数 $H(e^{j\omega })$：系统的“频率指纹”

一个LTI系统的频率响应 $H(e^{j\omega })$，是其系统函数 $H(z)$ 在单位圆 $|z|=1$ 上的取值：
$$H(e^{j\omega })=H(z){|}_{z=e^{j\omega }}$$
前提是单位圆必须包含在 $H(z)$ 的ROC内。

• $|H(e^{j\omega })|$ 是幅度响应，描述系统对不同频率信号的增益或衰减。
• $\angle H(e^{j\omega })$ 是相位响应，描述系统对不同频率信号的相位延迟。
• 通过分析 $H(e^{j\omega })$ 的幅度谱和相位谱，我们可以判断系统是低通、高通、带通、带阻等，以及它对信号相位的影响。

零极点分析频响特性：洞察系统行为的关键

Z 平面上的零点和极点分布，直观地揭示了系统的频率响应特性。

• 极点 (Poles)： 极点的位置决定了系统在某个频率附近的放大特性。
  • 如果一个极点靠近单位圆，那么在它对应的频率点（单位圆上与极点径向方向相同的点），幅度响应会显著增大。
  • 如果极点在单位圆上，则系统在该频率处会有无限大的增益，系统可能不稳定。
• 零点 (Zeros)： 零点的位置决定了系统在某个频率附近的衰减特性。
  • 如果一个零点靠近单位圆，那么在它对应的频率点，幅度响应会显著衰减。
  • 如果零点恰好落在单位圆上，那么在它对应的频率点，幅度响应为零，该频率分量会被系统完全“扼杀”（例如，陷波滤波器）。

因果性与稳定性判断：Z 变换的“诊断报告”

Z 变换和ROC为LTI系统的因果性和稳定性提供了非常直观的判据。

1. 因果LTI系统：

   • 其ROC必须是其最外层极点之外的区域（一个圆外部）。
   • 其单位脉冲响应 $h(n)$ 必须是右边序列。
   • 如果系统是因果的，且由差分方程描述，那么其 $H(z)$ 的所有极点都必须位于有限平面内（即没有无穷远的极点）。

2. 稳定LTI系统 (BIBO 稳定)：

   • 其ROC必须包含单位圆。
   • 其单位脉冲响应 $h(n)$ 必须是绝对可和的。

3. 因果且稳定LTI系统：

   • 如果一个LTI系统既因果又稳定，那么它的ROC必须是其最外层极点之外的区域，并且该区域必须包含单位圆。
   • 这意味着，对于因果LTI系统，其所有极点都必须位于单位圆之内。这是判断因果LTI系统稳定性的黄金法则！
   • 在控制系统中，系统的极点位置是决定其稳定性的关键。如果控制系统的极点位于单位圆外，系统就会发散，无法稳定运行。

总结与展望

在第二章，我们掌握了数字信号处理中至关重要的两大工具：

• 离散时间傅里叶变换 (DTFT)：让我们能够将时域信号分解为频率成分，理解信号的频率内容，并发现时域卷积对应频域乘积这一简化分析的“黄金法则”。
• Z 变换：作为DTFT的推广，它拥有更广阔的适用范围，并引入了收敛域 (ROC) 这一核心概念，使Z变换能够完整地描述序列。通过Z变换，我们能够轻松地求解差分方程，将复杂的时域问题转化为代数问题。

更重要的是，我们学习了如何利用系统函数 $H(z)$ 和其零极点在Z平面上的分布来分析LTI系统的频率响应、因果性和稳定性。特别是“因果LTI系统所有极点必须在单位圆内才稳定”这一结论，在数字滤波器设计和控制系统分析中具有指导性意义。

有了这些强大的变换工具，我们现在可以更深入地理解和设计数字信号处理系统了。然而，DTFT是一个连续函数，Z变换也是定义在连续的复平面上，它们在计算机中无法直接计算。这就引出了下一章的内容：离散傅里叶变换 (DFT)，它将是我们在数字世界中实际计算频谱的桥梁。敬请期待！

---

习题

学以致用，下面是几道练习题，帮助你巩固本章的知识点。

1. Z 变换和 ROC：
求序列 $x(n)=(0.8{)}^{n}u(n)+(1.2{)}^{n}u(-n-1)$ 的 Z 变换 $X(z)$ 及其 ROC。

2. 逆 Z 变换：
已知 Z 变换 $X(z)=\frac{1}{(1-0.5z^{-1})(1-2z^{-1})}$。
a) 如果 ROC 是 $|z|>2$，求 $x(n)$。
b) 如果 ROC 是 $|z|<0.5$，求 $x(n)$。
c) 如果 ROC 是 $0.5<|z|<2$，求 $x(n)$。

3. Z 变换解差分方程：
一个LTI系统由差分方程描述：$y(n)-0.25y(n-2)=x(n)$。
已知输入 $x(n)=\delta (n)$，且系统是因果的，所有初始条件为零。
a) 求系统函数 $H(z)$。
b) 求系统的单位脉冲响应 $h(n)$。

4. 系统稳定性与因果性：
一个LTI系统的系统函数为 $H(z)=\frac{z+1}{z^2-1.5z+0.5}$。
a) 绘制零极点图。
b) 如果系统是因果的，判断它是否稳定。
c) 如果系统是稳定的，判断它是否因果。

---

答案

1. Z 变换和 ROC：
对于 $x_1(n)=(0.8{)}^{n}u(n)$，$X_1(z)=\frac{1}{1-0.8z^{-1}}$，ROC 是 $|z|>0.8$。
对于 $x_2(n)=(1.2{)}^{n}u(-n-1)$，这是一个左边序列。
我们知道 $-(1.2{)}^{n}u(-n-1)$ 的 Z 变换是 $\frac{1}{1-1.2z^{-1}}$，ROC 是 $|z|<1.2$。
所以 $x_2(n)=-(1.2{)}^{n}u(-n-1)$ 对应 $X_2(z)=-\frac{1}{1-1.2z^{-1}}$，ROC 是 $|z|<1.2$。
根据线性性质，$X(z)=X_1(z)+X_2(z)=\frac{1}{1-0.8z^{-1}}-\frac{1}{1-1.2z^{-1}}$。
系统的 ROC 是两个子序列 ROC 的交集，即 $(|z|>0.8)\cap (|z|<1.2)=0.8<|z|<1.2$。
所以，$X(z)=\frac{1}{1-0.8z^{-1}}-\frac{1}{1-1.2z^{-1}}$，ROC 为 $0.8<|z|<1.2$。

2. 逆 Z 变换：
$X(z)=\frac{1}{(1-0.5z^{-1})(1-2z^{-1})}$
先进行部分分式展开：
$X(z)=\frac{A}{1-0.5z^{-1}}+\frac{B}{1-2z^{-1}}$
$1=A(1-2z^{-1})+B(1-0.5z^{-1})$
令 $z^{-1}=2$：$1=A(1-4)+B(1-1)=-3A\Rightarrow A=-1/3$
令 $z^{-1}=0.5$：$1=A(1-1)+B(1-0.25)=0.75B\Rightarrow B=4/3$
所以 $X(z)=\frac{-1/3}{1-0.5z^{-1}}+\frac{4/3}{1-2z^{-1}}$

a) 如果 ROC 是 $|z|>2$：
这意味着序列是右边序列。两项都对应右边序列的形式。
$x(n)=-\frac{1}{3}(0.5{)}^{n}u(n)+\frac{4}{3}(2{)}^{n}u(n)$

b) 如果 ROC 是 $|z|<0.5$：
这意味着序列是左边序列。两项都对应左边序列的形式。
$x(n)=-(-\frac{1}{3})(0.5{)}^{n}u(-n-1)+(-\frac{4}{3})(2{)}^{n}u(-n-1)$
$x(n)=\frac{1}{3}(0.5{)}^{n}u(-n-1)-\frac{4}{3}(2{)}^{n}u(-n-1)$

c) 如果 ROC 是 $0.5<|z|<2$：
这意味着第一项 $(1-0.5z^{-1}{)}^{-1}$ 对应右边序列（因为 $|z|>0.5$），第二项 $(1-2z^{-1}{)}^{-1}$ 对应左边序列（因为 $|z|<2$）。
$x(n)=-\frac{1}{3}(0.5{)}^{n}u(n)+(-\frac{4}{3})(2{)}^{n}u(-n-1)$
$x(n)=-\frac{1}{3}(0.5{)}^{n}u(n)-\frac{4}{3}(2{)}^{n}u(-n-1)$

3. Z 变换解差分方程：
差分方程：$y(n)-0.25y(n-2)=x(n)$
a) 求系统函数 $H(z)$：零初始条件，对差分方程进行 Z 变换。
$Y(z)-0.25z^{-2}Y(z)=X(z)$
$Y(z)(1-0.25z^{-2})=X(z)$
$H(z)=\frac{Y(z)}{X(z)}=\frac{1}{1-0.25z^{-2}}$

b) 求单位脉冲响应 $h(n)$：令 $x(n)=\delta (n)\Rightarrow X(z)=1$。
则 $Y(z)=H(z)=\frac{1}{1-0.25z^{-2}}$
因式分解分母：$1-0.25z^{-2}=(1-0.5z^{-1})(1+0.5z^{-1})$
$Y(z)=\frac{1}{(1-0.5z^{-1})(1+0.5z^{-1})}$
部分分式展开：
$Y(z)=\frac{A}{1-0.5z^{-1}}+\frac{B}{1+0.5z^{-1}}$
$1=A(1+0.5z^{-1})+B(1-0.5z^{-1})$
令 $z^{-1}=2$：$1=A(1+1)=2A\Rightarrow A=1/2$
令 $z^{-1}=-2$：$1=B(1+1)=2B\Rightarrow B=1/2$
所以 $Y(z)=\frac{1/2}{1-0.5z^{-1}}+\frac{1/2}{1+0.5z^{-1}}$
由于系统是因果的，ROC 是 $|z|>0.5$。因此两项都对应右边序列。
$h(n)=\frac{1}{2}(0.5{)}^{n}u(n)+\frac{1}{2}(-0.5{)}^{n}u(n)$

4. 系统稳定性与因果性：
$H(z)=\frac{z+1}{z^2-1.5z+0.5}$
a) 绘制零极点图：

• 零点：分子为零，即 $z+1=0\Rightarrow z_1=-1$。
• 极点：分母为零，即 $z^2-1.5z+0.5=0$。
  $(z-1)(z-0.5)=0\Rightarrow z_2=1,z_3=0.5$。
  在 Z 平面上：
• 零点在 $z=-1$ 处。
• 极点在 $z=0.5$ 和 $z=1$ 处。
  （绘制Z平面，画出单位圆，在 $z=-1$ 处画 O，在 $z=0.5$ 和 $z=1$ 处画 X。）

b) 如果系统是因果的，判断它是否稳定：
对于因果LTI系统，其ROC是最外层极点之外的区域。本系统的极点在 $z=0.5$ 和 $z=1$，因此因果系统的ROC是 $|z|>1$。
稳定性要求ROC包含单位圆。 由于ROC $|z|>1$ 不包含单位圆（因为 $z=1$ 在ROC的边界上，而不是内部），所以系统不稳定。

c) 如果系统是稳定的，判断它是否因果：
稳定性要求ROC包含单位圆。 极点在 $z=0.5$ 和 $z=1$。
为了使ROC包含单位圆，ROC 必须是 $0.5<|z|<1$ 或 $0.5<|z|<\infty$ （不包含 $z=1$ 的情况，需要考虑极点性质）。
由于 $z=1$ 处有一个极点，如果ROC包含单位圆，那么单位圆必须在极点 $z=1$ 的左边，且在极点 $z=0.5$ 的右边。
唯一的可能ROC是 $0.5<|z|<1$。
如果ROC是 $0.5<|z|<1$，这是一个环形区域，表示序列是双边序列。
因此，如果系统是稳定的，它将不是因果的 (因为因果系统的ROC必须是圆外区域)。