当前位置：首页 > news >正文

使用MATLAB求解微分方程：从基础到实践

news 2025/5/29 13:00:27

使用MATLAB求解微分方程：从基础到实践

微分方程是描述自然界和工程领域中许多现象的重要数学工具。MATLAB提供了强大的工具来求解各种类型的微分方程。本文将介绍如何使用MATLAB求解常微分方程(ODE)和偏微分方程(PDE)。

1. 基本ODE求解器

MATLAB提供了多种ODE求解器，最常用的是ode45，它基于Runge-Kutta方法。

%% 示例1：求解简单的一阶ODE dy/dt = -2y, y(0) = 1
clc
clear
closetspan = [0 5];  % 时间区间
y0 = 1;         % 初始条件
[t, y] = ode45(@(t,y) -2*y, tspan, y0);% 绘制结果
plot(t, y,'DisplayName', 'ode45解')
hold on
%绘制理论解
t=0:0.1:5;
y=exp(-2*t);
plot(t, y,'o','DisplayName', '理论解')
xlabel('t')
ylabel('y(t)')
title('Solution of dy/dt = -2y, y(0) = 1')
legend('show');

理论解法：
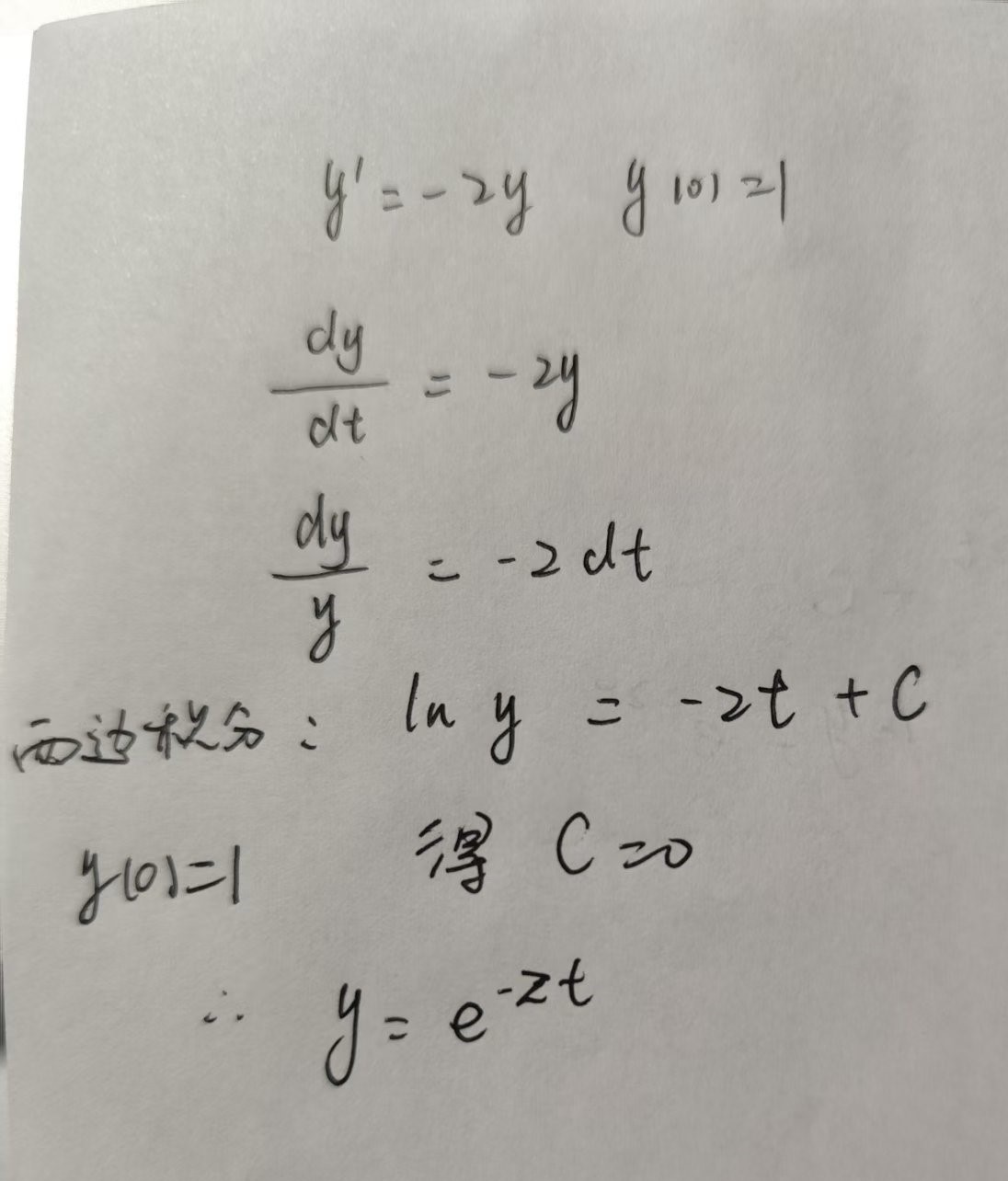
在这里插入图片描述
matlab求解结果：

2. 高阶ODE求解

对于高阶ODE，需要先将其转化为一阶方程组。例如，对于二阶ODE：

%% 示例2：求解阻尼振荡方程 d?y/dt? + 2ξωdy/dt + ω?y = 0
clc
clearomega = 2;    % 自然频率
xi = 0.1;     % 阻尼比% 转化为一阶方程组：
% y1 = y, y2 = dy/dt
% dy1/dt = y2
% dy2/dt = -2*xi*omega*y2 - omega^2*y1odefun = @(t,y) [y(2); -2*xi*omega*y(2) - omega^2*y(1)];
tspan = [0 10];
y0 = [1; 0];  % 初始位移和速度[t, y] = ode45(odefun, tspan, y0);alpha=-0.2;
beta=(16-0.16)^0.5/2;
c1=1
c2=-alpha/beta;
xx=0:0.1:10;
yy=exp(alpha.*xx).*(c1.*cos(beta.*xx)+c2.*sin(beta.*xx));
dy=exp(alpha.*xx).*(-c1.*beta.*sin(beta.*xx)+c2.*beta.*cos(beta.*xx)+...alpha*(c1.*cos(beta.*xx)+c2.*sin(beta.*xx)));% 绘制位移和速度
figure
subplot(2,1,1)
plot(t, y(:,1),'DisplayName', 'ode45解')
hold on
plot(xx,yy,'o','DisplayName', '理论解')
title('Displacement')
legend('show');
subplot(2,1,2)
plot(t, y(:,2),'DisplayName', 'ode45解')
hold on
plot(xx,dy,'o','DisplayName', '理论解')
title('Velocity')
legend('show');