卫星姿态描述基础知识学习记录(部分)

相对姿态(坐标系旋转)的描述：假设目标的坐标系为B,参考坐标系为R，对目标的姿态描述即确定目标坐标系与参考坐标系的关系。由于目标坐标系一般固结在目标上，这样便实现了目标的相对姿态描述。描述方式主要有：方向余弦式、欧拉轴/角式、欧拉角式、姿态四元数；由于姿态可唯一确定，这些描述方式间可相互转换。

1.方向余弦

其中Vr一般已知，Vb为测量值，C为所求。
思考：首先我们考虑旋转，矢量可以在空间平移；余弦与在各个轴上的投影相关；由于只关注旋转关系可以只从单位矢量角度考虑。

2.欧拉轴/角式

“欧拉定理：刚体绕固定点的任意位移(旋转)，可由绕通过此点的某一固定轴转动一定角度得到。”这时姿态描述参数共有4个，即转轴的单位矢量在参考坐标系下的三个方向余弦ex、ey、ez，以及绕轴转动的转角Φ(需要知道绕谁转，转了多少)。对于矩阵C一定有特征值为1的特征矢量(C为旋转矩阵，则其行列式必为1)，则必有单位矢量e满足：e=Ce(特征值求法：Qx=λx), 即刚体转轴方向的矢量e在目标坐标系和参考坐标系的分量相同。
【这里需要补充旋转矩阵以及正交矩阵相关概念：
(4 封私信) 旋转矩阵的行列式为什么等于1? - 知乎】
现在构架基于ex、ey、ez以及Φ的姿态描述：

3.欧拉角式

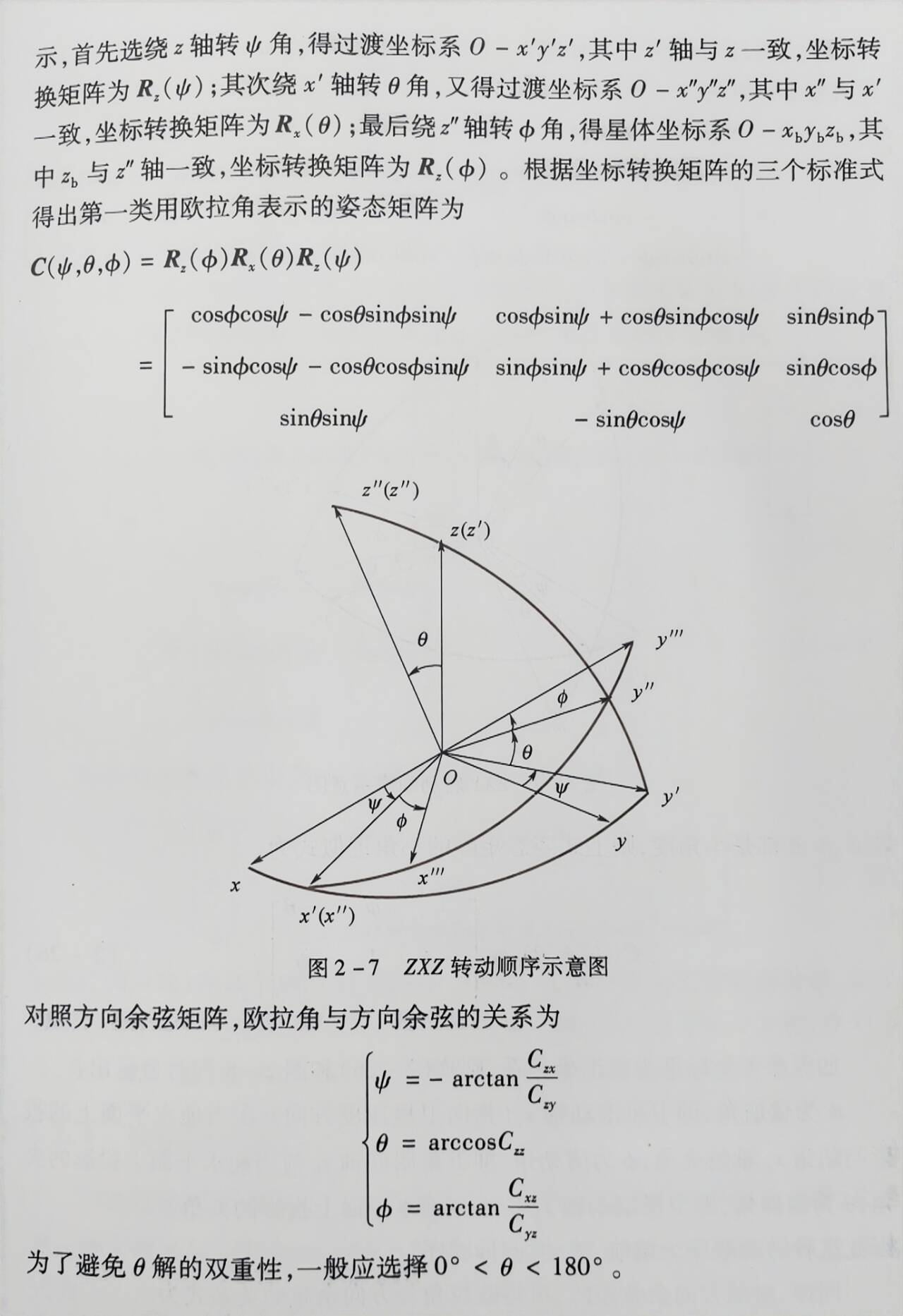
欧拉定理，刚体绕固定点的位移可以通过绕该点的若干次有限转动实现。将参考坐标系分别绕着自身三条坐标轴进行三次旋转，每次转动一个欧拉角，得到新的坐标系。这样姿态矩阵可由三次坐标转换矩阵的乘积。
绕三个轴转动的旋转矩阵如下：（X,Y,Z）

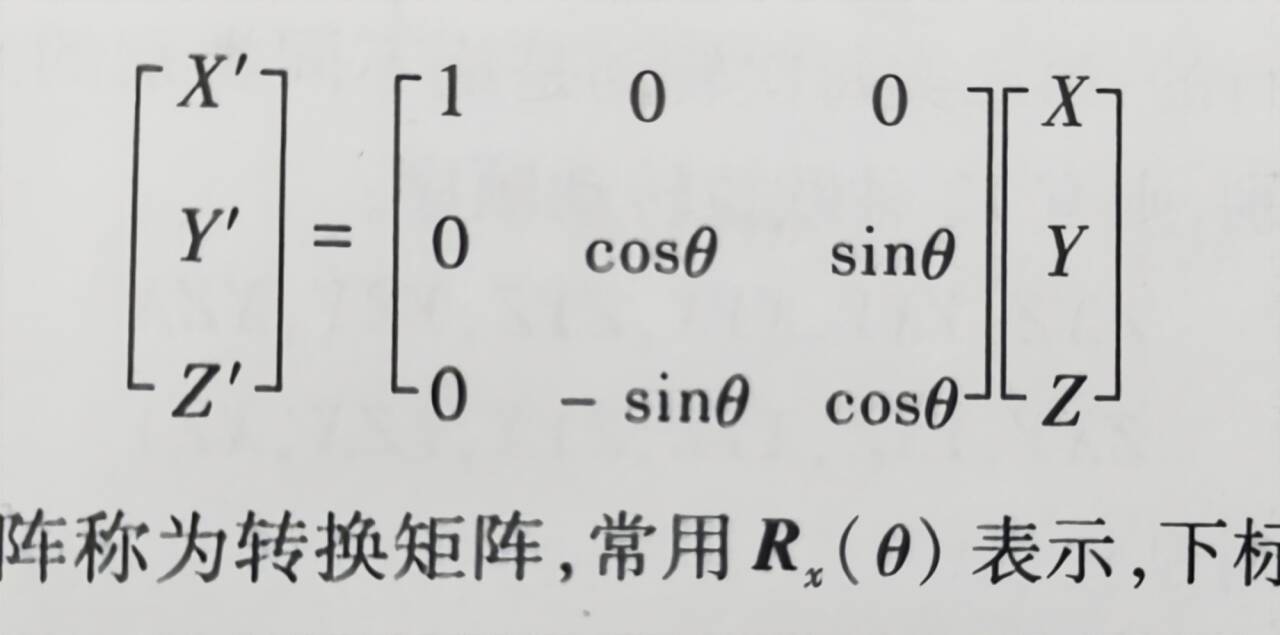
4.姿态四元数

用欧拉转轴/角参数组成的四元数表示姿态矩阵中的元素：
【注：】

机器人导论之转移算子及欧拉角 - 知乎

姿态的三种描述方式——欧拉角、轴角、四元数_姿态 的 4个值-CSDN博客

其他参考链接：机器人学——位置与姿态描述_位姿-CSDN博客
主要参考教材《卫星姿态测量与确定》