数据结构-图的应用，实现环形校验和拓扑排序

一、如何理解“图”？

1.什么是图？

图（Graph）是一种非线性数据结构，由顶点（Vertex）和边（Edge）组成。相较于线性关系（链表）和分治关系（树），网络关系（图）的自由度更高。

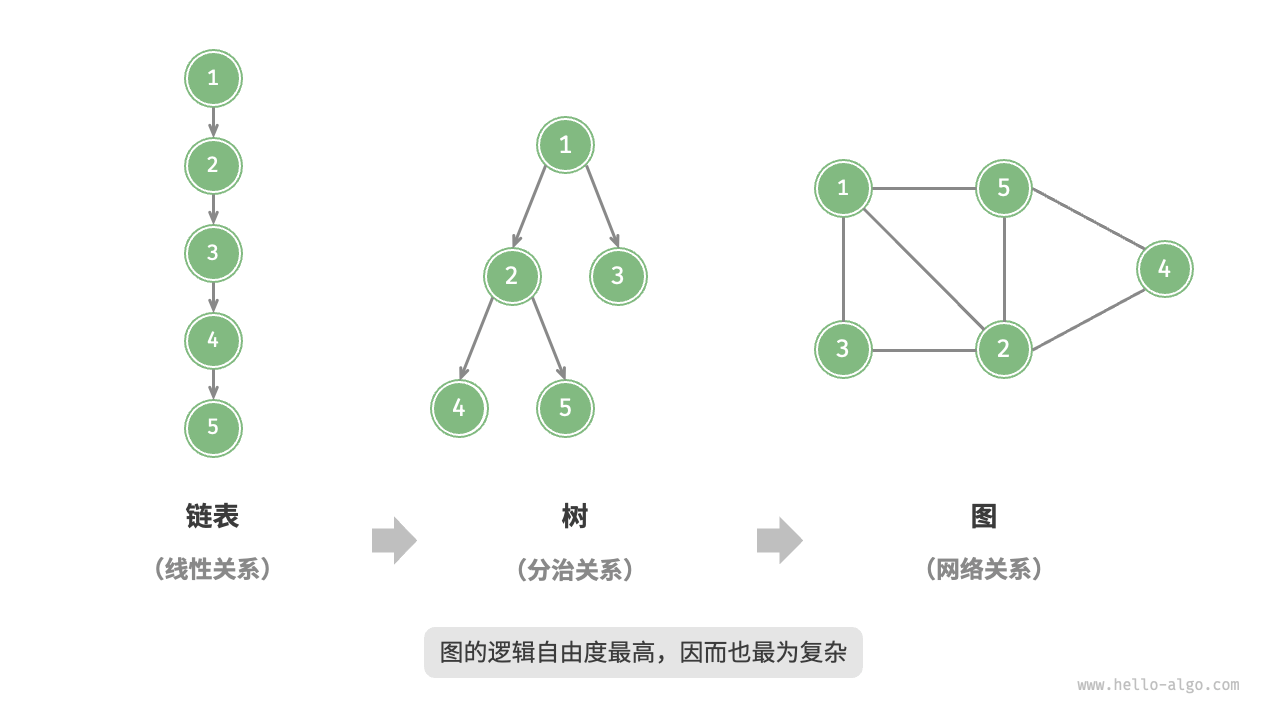
2.无向图和有向图

根据边是否具有方向，可分为无向图（undirected graph）和有向图（directed graph），如图 9-2 所示。

在无向图中，边表示两顶点之间的“双向”连接关系，例如微信或 QQ 中的“好友关系”。我们就拿微信举例子吧。我们可以把每个用户看作一个顶点。如果两个用户之间互加好友，那就在两者之间建立一条边。所以，整个微信的好友关系就可以用一张图来表示。其中，每个用户有多少个好友，对应到图中，就叫作顶点的度（Degree），就是跟顶点相连接的边的条数。

在有向图中，边具有方向性，两个方向的边是相互独立的，例如微博或抖音上的“关注”与“被关注”关系。
我们刚刚讲过，无向图中有“度”这个概念，表示一个顶点有多少条边。在有向图中，我们把度分为入度（In-degree）和出度（Out-degree）。
顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。

3.无权图和有权图

我们还可以为边添加“权重”变量，从而得到如图 9-4 所示的有权图（weighted graph）。例如在《王者荣耀》等手游中，系统会根据共同游戏时间来计算玩家之间的“亲密度”，这种亲密度网络就可以用有权图来表示。

二、JGraphT-图论数据结构和算法的 Java 库

https://jgrapht.org/

1.引入Maven依赖

<dependency><groupId>org.jgrapht</groupId><artifactId>jgrapht-core</artifactId><version>${org.jgrapht.core.version}</version>
</dependency>
<dependency><groupId>org.jgrapht</groupId><artifactId>jgrapht-ext</artifactId><version>${org.jgrapht.ext.version}</version>
</dependency><properties><org.jgrapht.core.version>1.5.2</org.jgrapht.core.version><org.jgrapht.ext.version>1.5.2</org.jgrapht.ext.version>
</properties>

2.环形校验

2.1 什么是循环依赖 ？

一个或多个对象之间存在直接或间接的依赖关系，这种依赖关系构成一个环形调用，有下面 3 种方式。

2.2 单元测试代码

首先创建DefaultDirectedGraph有向图对象，添加顶点和边。然后创建CycleDetector环形检测对象，并将graph对象传入，调用detectCycles()方法就很容易实现环形检测。

package com.baeldung.jgrapht;import com.mxgraph.layout.mxCircleLayout;
import com.mxgraph.layout.mxIGraphLayout;
import com.mxgraph.util.mxCellRenderer;
import org.jgrapht.Graph;
import org.jgrapht.alg.cycle.CycleDetector;
import org.jgrapht.ext.JGraphXAdapter;
import org.jgrapht.graph.DefaultDirectedGraph;
import org.jgrapht.graph.DefaultEdge;
import org.junit.jupiter.api.Test;import javax.imageio.ImageIO;
import java.awt.*;
import java.awt.image.BufferedImage;
import java.io.File;
import java.io.IOException;
import java.util.Set;import static org.junit.jupiter.api.Assertions.*;public class DetectCyclesUnitTest {/*** 情况1：自己依赖自己*/@Testpublic void testA() {DefaultDirectedGraph<String, DefaultEdge> graph = new DefaultDirectedGraph<>(DefaultEdge.class);graph.addVertex("A");graph.addEdge("A", "A");CycleDetector<String, DefaultEdge> cycleDetector = new CycleDetector<>(graph);assertTrue(cycleDetector.detectCycles());assertTrue(cycleDetector.findCycles().contains("A"));generateImage(graph, "情况1：自己依赖自己");}/*** 情况2：两个对象之间*/@Testpublic void testB() {DefaultDirectedGraph<String, DefaultEdge> graph = new DefaultDirectedGraph<>(DefaultEdge.class);graph.addVertex("A");graph.addVertex("B");graph.addEdge("A", "B");graph.addEdge("B", "A");CycleDetector<String, DefaultEdge> cycleDetector = new CycleDetector<>(graph);assertTrue(cycleDetector.detectCycles());assertEquals(2, cycleDetector.findCycles().size());generateImage(graph, "情况2：两个对象之间");}/*** 情况3：多个对象之间*/@Testpublic void testC() {DefaultDirectedGraph<String, DefaultEdge> graph = new DefaultDirectedGraph<>(DefaultEdge.class);graph.addVertex("A");graph.addVertex("B");graph.addVertex("C");graph.addEdge("A", "B");graph.addEdge("B", "C");graph.addEdge("C", "A");CycleDetector<String, DefaultEdge> cycleDetector = new CycleDetector<>(graph);assertTrue(cycleDetector.detectCycles());assertEquals(3, cycleDetector.findCycles().size());generateImage(graph, "情况3：多个对象之间");}/*** 真实情况*/@Testvoid testX() {DefaultDirectedGraph<String, DefaultEdge> directedGraph = new DefaultDirectedGraph<>(DefaultEdge.class);directedGraph.addVertex("v1");directedGraph.addVertex("v2");directedGraph.addVertex("v3");directedGraph.addVertex("v4");directedGraph.addVertex("v5");directedGraph.addVertex("v6");directedGraph.addEdge("v2", "v1");directedGraph.addEdge("v4", "v1");directedGraph.addEdge("v5", "v1");directedGraph.addEdge("v6", "v1");directedGraph.addEdge("v3", "v2");directedGraph.addEdge("v1", "v3");CycleDetector<String, DefaultEdge> cycleDetector = new CycleDetector<>(directedGraph);assertTrue(cycleDetector.detectCycles());Set<String> cycleVertices = cycleDetector.findCycles();assertFalse(cycleVertices.isEmpty());generateImage(directedGraph, "真实情况");}/*** 生成图片** @param graph     图* @param imageName 图片名*/public static void generateImage(Graph graph, String imageName) {JGraphXAdapter<String, DefaultEdge> graphAdapter = new JGraphXAdapter<>(graph);mxIGraphLayout layout = new mxCircleLayout(graphAdapter);layout.execute(graphAdapter.getDefaultParent());File imgFile = new File("src/test/resources/" + imageName + ".png");BufferedImage image = mxCellRenderer.createBufferedImage(graphAdapter, null, 2, Color.WHITE, true, null);try {ImageIO.write(image, "PNG", imgFile);} catch (IOException e) {//ignore}}
}

2.3 情况1：自己依赖自己

A依赖于A

2.4 情况2：两个对象之间

A依赖于B，B依赖于A

2.5 情况3：多个对象之间

A依赖于C，B依赖于A，C依赖于B

2.6 情况4：真实情况

说是真实情况，但生产非常大的可能性会比这个复杂，我们用这个引出拓扑排序。

3.拓扑排序

3.1 Kahn算法

Kahn算法实际上用的是贪心算法思想，思路非常简单、好懂。

定义数据结构的时候，如果s需要先于t执行，那就添加一条s指向t的边。所以，如果某个顶点入度为0， 也就表示，没有任何顶点必须先于这个顶点执行，那么这个顶点就可以执行了。

我们先从图中，找出一个入度为0的顶点，将其输出到拓扑排序的结果序列中（对应代码中就是把它打印出来），并且把这个顶点从图中删除（也就是把这个顶点可达的顶点的入度都减1）。我们循环执行上面的过程，直到所有的顶点都被输出。最后输出的序列，就是满足局部依赖关系的拓扑排序。

我把Kahn算法用代码实现了一下，你可以结合着文字描述一块看下。不过，你应该能发现，这段代码实现更有技巧一些，并没有真正删除顶点的操作。代码中有详细的注释，你自己来看，我就不多解释了。

3.2 Lua版

拓扑排序应用非常广泛，解决的问题的模型也非常一致。凡是需要通过局部顺序来推导全局顺序的，一般都能用拓扑排序来解决。除此之外，拓扑排序还能检测图中环的存在。对于Kahn算法来说，如果最后输出出来的顶点个数，少于图中顶点个数，图中还有入度不是0顶点，那就说明，图中存在环。

local func_map = {f_A = { "f_B" },f_B = { "f_C" }
}local func_map_len = table_len(func_map)
local sorted_funcs = {}local function build_dag(func_deps)local dag = {}local in_degrees = {}for func, deps in pairs(func_deps) dodag[func] = dag[func] or {}in_degrees[func] = in_degrees[func] or 0for _, dep in pairs(deps) dodag[dep] = dag[dep] or {}in_degrees[dep] = in_degrees[dep] or 0table.insert(dag[dep], func)in_degrees[func] = in_degrees[func] + 1endendreturn dag, in_degrees
endlocal function build_sorted_funcs(dag, in_degrees)local zero_in_degree_queue = {}local sorted_funcs = {}for func, in_degree in pairs(in_degrees) doif in_degree == 0 thentable.insert(zero_in_degree_queue, func)endendwhile #zero_in_degree_queue > 0 dolocal func = table.remove(zero_in_degree_queue, 1)table.insert(sorted_funcs, func)for _, parent in pairs(dag[func]) doin_degrees[parent] = in_degrees[parent] - 1if in_degrees[parent] == 0 thentable.insert(zero_in_degree_queue, parent)endendendreturn sorted_funcs
endlocal dag, in_degrees = build_dag(func_map)
sorted_funcs = build_sorted_funcs(dag, in_degrees)function invoke(...)if #sorted_funcs == func_map_len thenfor _, func in ipairs(sorted_funcs) domud_sense[func]()endelseprint("error: graph with loop")endreturn "OK"
end

由于上面的代码是车端执行的，为了节约算力，云端在代码生成后直接给出顺序，大大减少了终端设备的计算。

local sorted_funcs = {"f_A","f_B","f_C"
}
function invoke(...)for _, func in ipairs(sorted_funcs) domud_sense[func]()endreturn "OK"
end

3.3 Java版

例子如下：

由于DefaultEdge中getSource()和getTarget()访问权限是protected，没有办法获取到相关的值，所有我自己继承了DefaultEdge，创建了MyEdge类。

package com.baeldung.jgrapht;import org.jgrapht.graph.DefaultEdge;public class MyEdge extends DefaultEdge {@Overridepublic String getSource() {return super.getSource().toString();}@Overridepublic String getTarget() {return super.getTarget().toString();}
}

首先初始化DefaultDirectedGraph相关顶点和边的数据。实现了两种拓扑排序：借助java API和借助jgrapht API

package com.baeldung.jgrapht;import lombok.extern.slf4j.Slf4j;
import org.jgrapht.alg.cycle.CycleDetector;
import org.jgrapht.graph.DefaultDirectedGraph;
import org.junit.jupiter.api.BeforeAll;
import org.junit.jupiter.api.Test;import java.util.*;import static com.baeldung.jgrapht.DetectCyclesUnitTest.generateImage;
import static org.junit.jupiter.api.Assertions.assertFalse;
import static org.junit.jupiter.api.Assertions.assertTrue;/*** 拓扑排序** @author xxx* @see* @since 1.0.0*/
@Slf4j
public class TopologicalSortUnitTest {private final static DefaultDirectedGraph<String, MyEdge> graph = new DefaultDirectedGraph<>(MyEdge.class);@BeforeAllpublic static void init() {graph.addVertex("v1");graph.addVertex("v2");graph.addVertex("v3");graph.addVertex("v4");graph.addVertex("v5");graph.addVertex("v6");graph.addEdge("v2", "v1");graph.addEdge("v4", "v1");graph.addEdge("v5", "v1");graph.addEdge("v6", "v1");graph.addEdge("v3", "v2");
//        graph.addEdge("v1","v3");}/*** 拓扑排序：借助java API*/@Testvoid test1() {CycleDetector<String, MyEdge> cycleDetector = new CycleDetector<>(graph);assertFalse(cycleDetector.detectCycles());Set<String> cycleVertices = cycleDetector.findCycles();assertTrue(cycleVertices.isEmpty());generateImage(graph, "拓扑排序");//转换Map<String, Set<String>> incomingVertax = new HashMap<>();for (String func : graph.vertexSet()) {incomingVertax.putIfAbsent(func, new TreeSet<>());}Set<MyEdge> defaultEdges = graph.edgeSet();for (MyEdge myEdge : defaultEdges) {incomingVertax.putIfAbsent(myEdge.getTarget(), new TreeSet<>());incomingVertax.get(myEdge.getTarget()).add(myEdge.getSource());}Map<String, Set<String>> outgoingVertax = buildOutgoingVertax(incomingVertax);Map<String, Integer> inDegrees = buildInDegrees(incomingVertax);List<String> result = buildSortedFunctions(outgoingVertax, inDegrees);System.out.println(result);}/*** 拓扑排序：借助jgrapht API*/@Testpublic void test2() {Queue<String> zeroInDegreeQueue = new LinkedList<>();Set<String> vertexSet = graph.vertexSet();List<String> sortedFunctions = new ArrayList<>();//构建入度Map<String, Integer> indegreeMap = new HashMap<>(vertexSet.size());for (String vertex : vertexSet) {indegreeMap.put(vertex, graph.inDegreeOf(vertex));if (graph.inDegreeOf(vertex) == 0) {zeroInDegreeQueue.add(vertex);}}while (!zeroInDegreeQueue.isEmpty()) {String v = zeroInDegreeQueue.poll();sortedFunctions.add(v);Set<MyEdge> defaultEdges = graph.outgoingEdgesOf(v);for (MyEdge defaultEdge : defaultEdges) {String parent = defaultEdge.getTarget();indegreeMap.put(parent, indegreeMap.get(parent) - 1);if (indegreeMap.get(parent) == 0) {zeroInDegreeQueue.add(parent);}}}System.out.println(sortedFunctions);}/*** 构建出度顶点** @param incomingVertax 入度顶点* @return 每个顶点的出度顶点*/private static Map<String, Set<String>> buildOutgoingVertax(Map<String, Set<String>> incomingVertax) {Map<String, Set<String>> outgoingVertax = new HashMap<>();for (String func : incomingVertax.keySet()) {outgoingVertax.putIfAbsent(func, new TreeSet<>());for (String dep : incomingVertax.get(func)) {outgoingVertax.putIfAbsent(dep, new TreeSet<>());outgoingVertax.get(dep).add(func);}}return outgoingVertax;}/*** 构建入度** @param incomingVertax 入度顶点* @return 每个顶点的入度数*/private static Map<String, Integer> buildInDegrees(Map<String, Set<String>> incomingVertax) {Map<String, Integer> inDegrees = new HashMap<>();for (String func : incomingVertax.keySet()) {inDegrees.putIfAbsent(func, 0);for (String dep : incomingVertax.get(func)) {inDegrees.putIfAbsent(dep, 0);inDegrees.put(func, inDegrees.get(func) + 1);}}return inDegrees;}/*** 构建排序函数** @param outgoingVertax 出度顶点* @param inDegrees      每个顶点的入度数* @return 拓扑排序结果*/private static List<String> buildSortedFunctions(Map<String, Set<String>> outgoingVertax, Map<String, Integer> inDegrees) {Queue<String> zeroInDegreeQueue = new LinkedList<>();List<String> sortedFunctions = new ArrayList<>();for (Map.Entry<String, Integer> entry : inDegrees.entrySet()) {if (entry.getValue() == 0) {zeroInDegreeQueue.add(entry.getKey());}}while (!zeroInDegreeQueue.isEmpty()) {String func = zeroInDegreeQueue.poll();sortedFunctions.add(func);for (String parent : outgoingVertax.get(func)) {inDegrees.put(parent, inDegrees.get(parent) - 1);if (inDegrees.get(parent) == 0) {zeroInDegreeQueue.add(parent);}}}return sortedFunctions;}
}

三、参考

https://www.hello-algo.com/chapter_graph/graph/
https://www.baeldung.com/jgrapht
https://www.51cto.com/article/716548.html