当前位置：首页 > news >正文

高效掌握二分查找：从基础到进阶

news 2025/5/20 5:38:19

前言

路漫漫其修远兮，吾将上下而求索；

这是题集，大家可以先尝试做一下：

704. 二分查找
34. 在排序数组中查找元素的第一个和最后一个位置
35. 搜索插入位置
69. x 的平方根
852. 山脉数组的峰顶索引
162. 寻找峰值
153. 寻找旋转排序数组中的最小值
LCR 173. 点名

做题之前，我们先介绍一下什么是二分算法；

特点：细节处理的比较多，容易写出死循环；

不仅数组有序的情况下可以使用二分，数组无序的情况下也可以使用二分；核心在于：只要数组中有规律能够使用二分进行查找，便就可以使用二分；

二分查找相关的模板有3个：

1、朴素的二分查找
2、查找左边界的二分模板
3、查找右边界的二分模板

我们先了解一下朴素的二分查找模板，剩下两个在做题中掌握然后再总结；

需要注意的是，我们在计算中间mid 的时候： int mid = left +(right-left)/2; 当然也可以写做：int mid = left + (right - left +1)/2; 这两种写法的区别在于[left,right] 区间中的数据个数为奇数、偶数的时候,如下图：

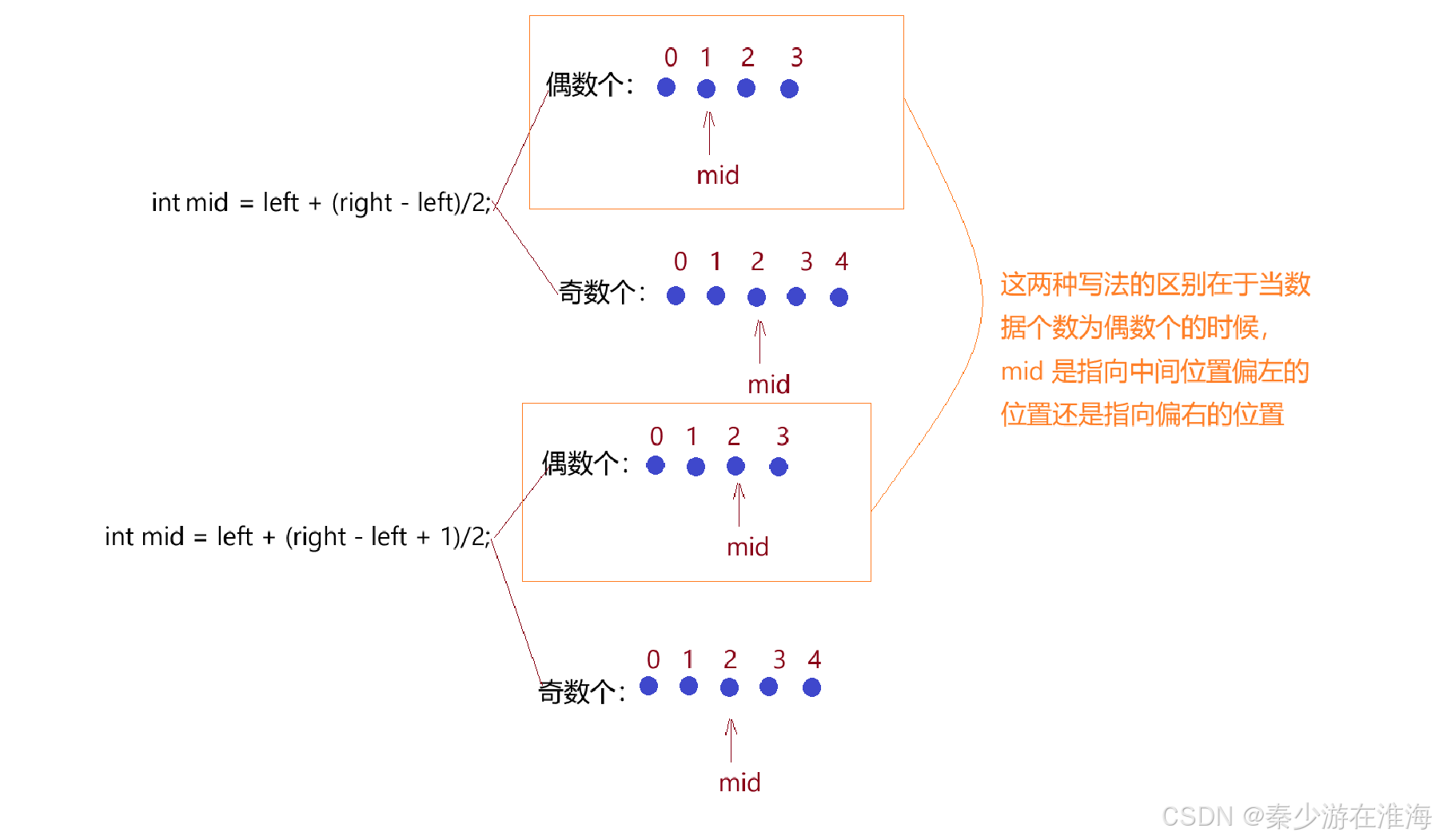
在朴素版本中，将中间点定义在何处都是一样的；以上两种计算中间点的方法均可适用，因为朴素的二分的核心在于：找到一个分界点，然后根据这个分界点来划分左、右区间，并不会关心中间点的位置是偏左还是偏右；

题1 二分查找：

704. 二分查找 - 力扣（LeetCode）

题干：

思考：

解法一：暴力解法

从左往右遍历该数组一遍，找到target 便停止操作，此时返回下标即可；倘若遍历完了整个数组均没有找到，就返回-1;

解法二：利用二分查找的思想

本题给的数组中的数据就是有序的；

在一个数组中找mid (可以将mid 当作为一种标识)，将mid 指向地数据与target 进行比较，而以mid 为分界线，该数组被划分为了两个区域，比nums[mid] 小的，比nums[mid] 大的；其中，我们可以根据target 与 nums[mid] 的大小关系而排除一个区域，而继续去另外一个没有排除的区域中查找……那么此时就可以认为数据具有二段行，从而可以使用二分法来解决；

二分查找的本质：当数据具有二分性的时候，与数组中的数据是否有序无关，如下：

关于mid,我们仅仅是将它当作一个分界线标志：

选择 1/2 ，是因为涉及数学中的概率学问题，即求数学期望，选择1/2t 的位置，算法的时间复杂度最好；

因为我们要频繁地找中点，并且频繁地确定接下来所要查找target 地区间，所以我们可以定义三指针：left,指向区间的左端点；right ，指向区间的右端点; mid , 表示区间的中点；

假设mid 指向的值为x ，那么x 与 target 就有三种大小关系，如下：

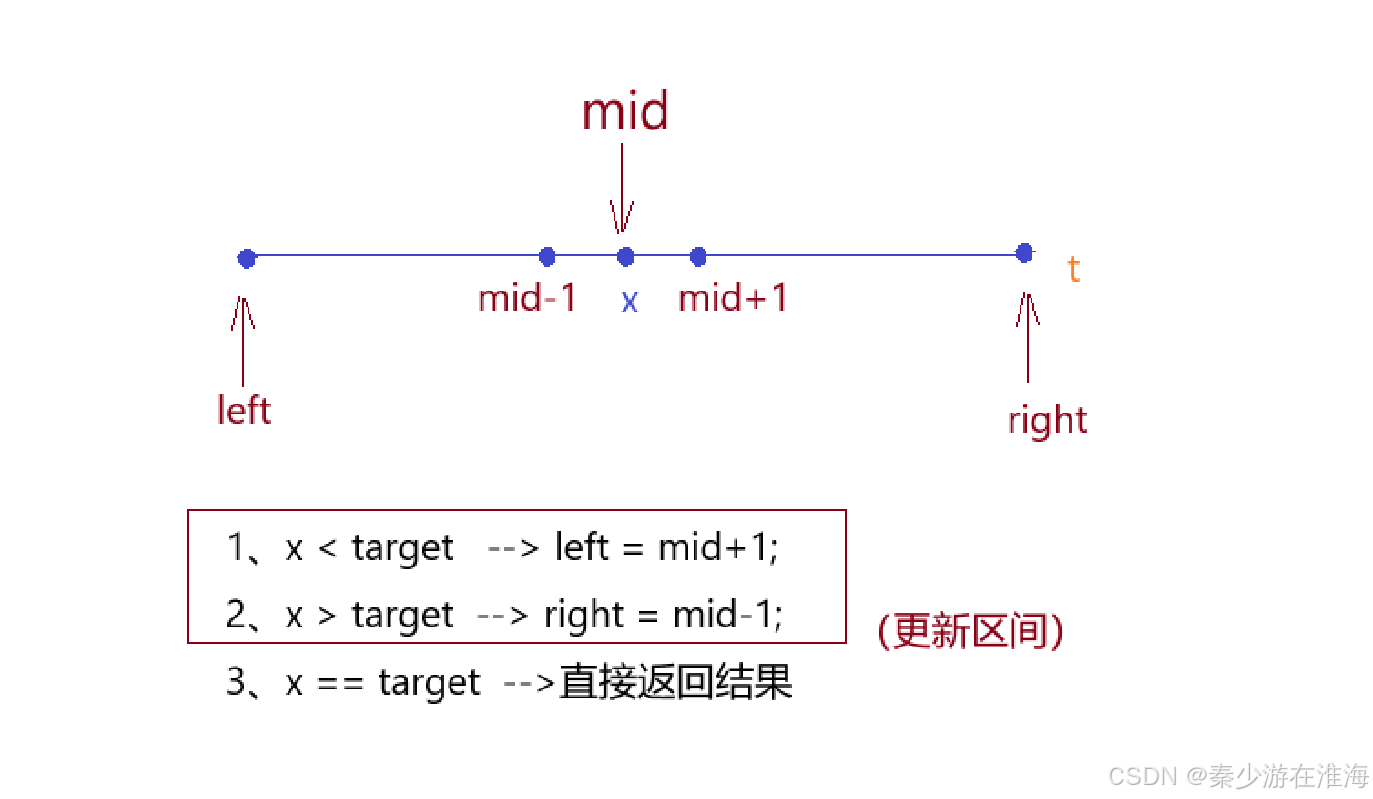
此处还存在许多细节问题：

Q1：循环结束的条件是什么？

当left 和right 维护的区间之中只有一个数据的时候，该数据仍需与target 进行比较；所以循环结束的条件： left<=right;

Q2：该二分查找算法为什么是正确的呢？

二分查找本质是从暴力解法上进行优化的；暴力解法既然正确，那么二分也一定正确；

Q3：该算法的时间复杂度？

最差就是该数组中没有所要查找的数据或者就在最后一次找个目标数据，所要查找的次数为 $\log_{2}N$ ,所以时间复杂度为 O(logN);

参考代码：

    int search(vector<int>& nums, int target) {int n = nums.size();int left = 0, right = n-1;while(left <= right){int mid = left + (right-left)/2;if(nums[mid]<target) left = mid+1;else if(nums[mid] > target) right = mid-1;else return mid;}//走到这里就是没有找到return -1;}

题2 在排序数组中查找元素的第一个和最后一个位置：

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题干：

思考：

题干中说的非递减顺序排序的意思就是该序列要么递增，要么相等；

解法一：暴力解法

从前往后遍历，遇到第一个等于target 的值时用变量begin 标记其下标，然后再用end 标记其结尾，当遍历完begin 和 end 均没有所要维护的区间的时候，说明没有找到，返回{-1,-1} 就可以了；

解法二：朴素二分

根据中间值(mid 所指向的值)进行分情况讨论；

但是只是利用mid 就只能找到与target 相等的值，并不能找到值与target 相等的区间；就需要去mid 的前、后继续查找；当整个数组中的值均为target的时候，此时的实践复杂度为O(N)；

朴素的二分最然也可以解决问题，但是在此处解决问题就失去了二分查找速度快的特性；

解法三：在朴素二分上进行优化

还记得前面我们所说的二分查找的本质吗？二分查找的本质是二段性；

我们将题干要求划分为两个小目标：1、查找左区间端点 2、查找右区间端点

part1:查找左区间端点

当我们找左端点时，该左端点的数据全是小于target 的，而其右边均是大于等于target 的，显然地将数据分为了两段，如下图：

朴素二分怎么做的呢？

情况二，当x <=t 的时候，mid 指向的数据可能刚好等于t ,那么将right 更新为 mid -1 ,便会少记录一个数据的范围 , 故而就不能直接将right 更新为mid -1; 而是让right 更新到mid 的位置即可；

即：

在朴素二分之中进行了修正，当nums[mid] 小于target 的时候，更新的策略不变: left = mid +1；但是当nums[mid] >= target 的时候，因为mid 指向的数据有可能等于target ，所以更新策略为 right = mid;

用这样的策略来解决问题还需要注意有两个细节需要处理：1、循环条件 2、求中间点的操作

Q: 这两个条件该选哪一个？

分情况讨论left 、right 区间：

ret 为最左端点的位置;

1、当left 与 right 区间中有结果；

当left 开始在不合法区间，而right 处于合法区间（left 一直在不合法的区间移动，right 一直在合法的区间移动）；而right 在合法区间移动一定不会超过ret 这个点，即right 永远都是大于等于target 的，而left 是永远想要跳过左边不合法的区域；那么left 与 right 相遇的位置一定是ret ，即当left 与 right 相等的时候该下标就是左区间的最终结果，无需判断，直接返回即可；故而从这一情况来看，循环条件应该为 left < right;

2、left 与 right 之间全是大于等于目标值target 的；

此时right 只会向左移动直到移动到与left 相遇为止；而当left 等于right 的时候，只需要判断left 指向的为止是否等于target 就可以了；如果等于target ，则说明该位置就是最终结果；不相等则返回{-1,-1}即可；并不需要进入循环之中判断当left == right 时，left 指向的数据是否为 target ;所以，就此情况而言，其循环条件也是 left < right;

3、left 与 right 区间之中全是小于目标值target 的

此时right 永远不会动而left 会一直向右移动；当 left == right 时，也不用进入循环之中判断，在循环外判断是否与target 相等就可以了；（此处一定不等于target ，因为[left,right] 之间全是小于target 的数据）；

经过以上分情况分析，循环条件应该选择： left < right；因为当left == right 的时候就是最终结果，在循环外面判断即可，倘若进入循环中判断便会造成死循环，如下：

2、求中间点的操作

此处有两种方式来求中间点：

这两种形式的区别，无非就是当数据个数为偶数个的时候，用方法一求得的mid 是偏左位置的中间点，而用方法二求得的mid 是偏右位置的中间点；在朴素二分中无论是用方法一还是方法二来求中间点均可，但是在此处不行；为什么呢？当最后一次操作，数组中刚好只剩下两个数据的时候，如下图：

经过上述的分析，求区间左端点更适合使用方法一来求中间点；

查找左端点的两个细节问题；

一是注意循环条件必为： left < right ;倘若left == right ,就已经是最终结果了，不用再进入循环进行判断；如果进入循环判断了就会陷入死循环；
二是求中间点的计算方式必须是： mid = left + (right - left)/2; 即当数据个数为偶数个的时候，中间点需要偏左；

part2:查找右区间端点

假设中间点mid 指向的值为 x

将x 与 target 之间的大小关系进行分情况讨论；

因为是要找右区间端点即：左边的区域均是小于等于target 的，右边的区域均是大于target 的；所以划分依据变成了 x <=t 与 x>t;
当 x <= t 的时候，更新left ,因为此时mid 指向的数据可能等于 target ，所以left 的更新并不是 mid+ 1, 而是 left = mid;

(总结如下图)

当x >t 的时候，更新right ，right = mid-1;

同样地需要处理两个细节问题：1、循环条件 2、求中间点的方式

此处对于循环条件地分析和查找区间左端点循环条件地分析一模一样，此处就不再赘述；

关于求中间点：

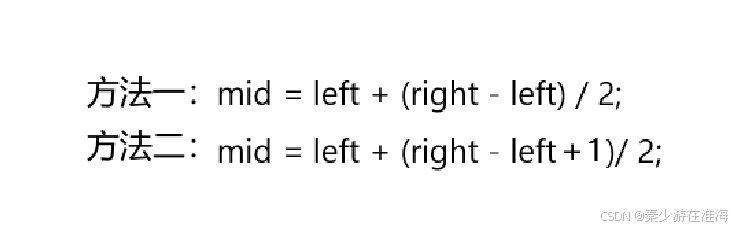
究竟是使用方法一还是方法二呢？

根据分析，当求区间右端点的时候更适合用方法二来求中间点；

思路总结：

同理，对于查找右端点的方法依旧是利用区间的二段性，即左边的区域均是小于等于target 的，右边的区域均是大于target 的，因此就可以使用二分来解决；其次在利用二分的时候，是在朴素二分的基础上更新了策略：当 x <= t , left = mid; 当x >t , right= mid-1;

查找左、右端点总结：

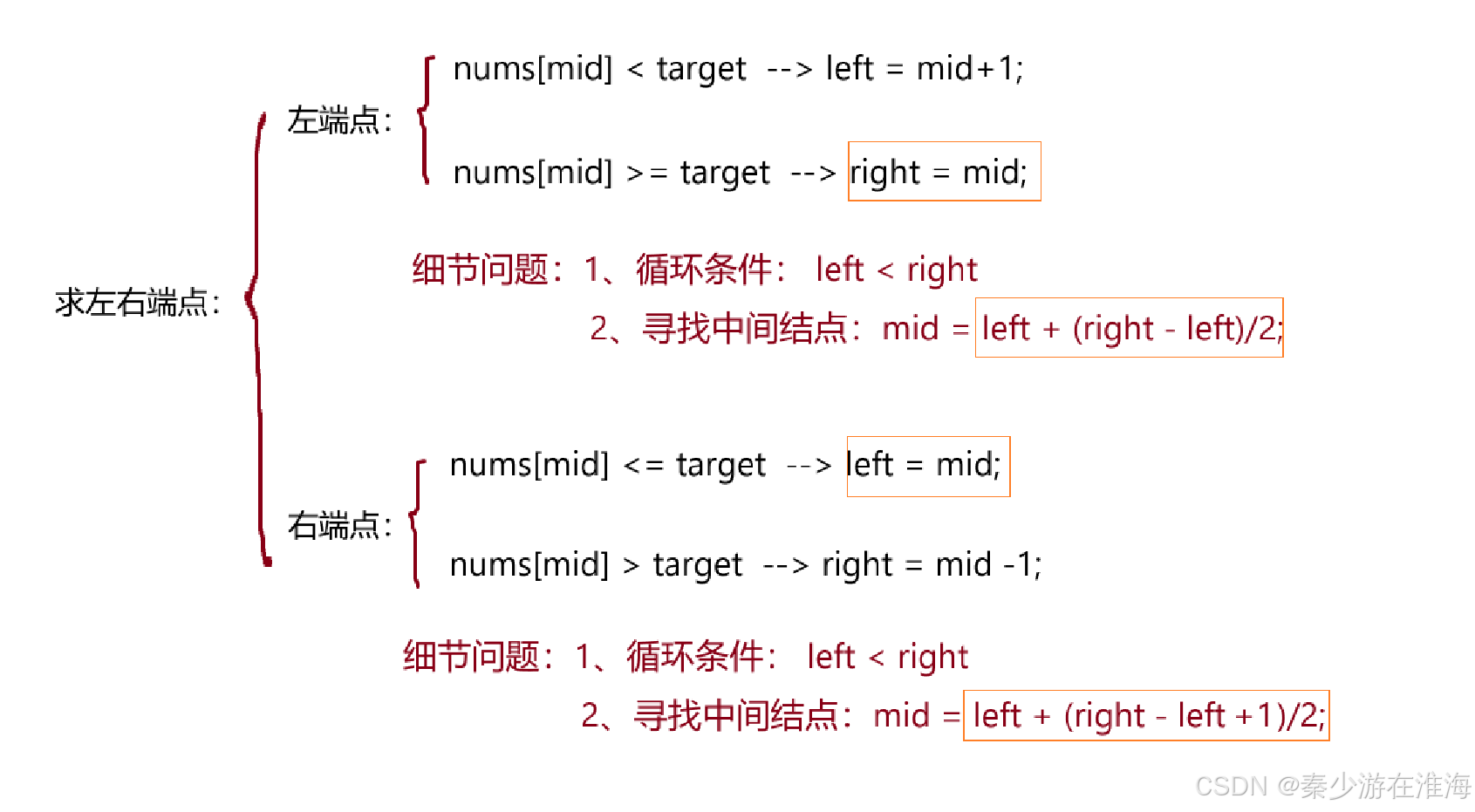
其实这就是剩下的两个模板：查找区间左端点的模板、查找区间右端点的模板：

记忆小技巧：下面出现-1 的时候，求mid 便会有 +1;

参考代码：

    vector<int> searchRange(vector<int>& nums, int target) {int n = nums.size();if(n==0) return {-1,-1};int left = 0, right = n-1,begin = 0 , end = 0;//寻找区间左端点//左端点-> 左边均是小于 t,右边是大于等于t//        left = mid +1;       right = mid;// 让mid 位于偏左的位置上 ： mid = left + (right - left)/2;while(left < right){int mid = left + (right - left )/2;if(nums[mid]<target) {left = mid+1;}else //nums[mid] >= target{right = mid;}}//出了循环就是left == right,判断指向的数据是否等于targetif(nums[left] == target) begin = left;else return{-1,-1};//寻找区间右端点//右端点 --> 左边均是小于等于t , 右边均是大于t//         left = mid;            right = mid -1;// 让mid 位于偏右的位置上， mid = left + (right - left+1)/2left = 0, right = n-1;while(left < right){int mid = left + (right - left +1)/2;if(nums[mid]<=target) {left = mid;}else //nums[mid] > target{right = mid -1;}}end = right;//写left 和 right 都是一样的return {begin , end};}

题3 搜索插入位置：

35. 搜索插入位置 - 力扣（LeetCode）

题干：

思考：

解法一：暴力解法

直接按照数据的升序进行查找，虽然时间复杂度不符合要求，但不失为一种方法；

解法二：二分（利用二段性）

此题分为两种情况，一是可以找到目标值，而是找不到目标值，但是需要返回这个目标值需要插入的位置，而所要插入的位置又有区分：越界、未越界（第一次出现比目标值大的数据）；

结合起来就是寻找大于等于目标值target 数据的下标；

可见该数据具有二段性，一段是小于target 的，一段是大于等于target 的；

我们要找到的是大于等于target 的第一个数据的下标；如果整个数组均是小于target 的数据，那么就返回这个数组的个数；

那么我们此处可以使用查找区间左端点的模板来解决；

我们先来回忆下下这个模板，首先是这个区间的划分依据：其左边是小于target 的，右边是大于等于target 的，假设指针mid 指向的数据未x; 当 x < target 的时候， left = mid +1; 但 x >= target 的时候，right = mid; 因为是right = mid , 为了避免死循环，中间点的计算应该偏左，即计算中间点： mid = left + (right-left)/2; 同样地，还可以通过我们地小技巧来记忆，因为left 和 right 中没有-1 ，所以计算mid 的方式不用加一；求区间左端点的伪代码如下：

参考代码：

    int searchInsert(vector<int>& nums, int target) {//使用二分查找区间左端点的代码模板int n = nums.size();int left = 0, right = n-1;while(left < right){int mid = left + (right - left)/2;if(nums[mid] < target) left = mid+1;else right = mid;}if(nums[left]<target) return n;else return left;}

题4 x 的平方根：

69. x 的平方根 - 力扣（LeetCode）

题干：

思考：

求一个数x的平方根，结果的平方一定小于等于x;

解法一：暴力解法

枚举1~x 的数据，然后依次计算平方根，从左往右暴力查找与x 最接近且小于等于x 的数；

例如，x = 17;

在枚举的过程，数据本身就是有序的，且符合二段性；即我们可以将数据划分为小于等于target 以及大于target 两段；

解法二：二分（利用二段性）

即本题我们可以利用查找区间右端点的模板来解决；

我们先来回忆一下查找右端点的模板，我们会将数据划分为两段，其左边小于等于目标值target ，其右边会大于目标值target ，假设指针mid 指向的数据为x;当 x <= target 的时候， left = mid;当 x > target 的时候，right = mid -1; 只有两个结点的时候，要避免 left == mid ，所以计算的mid 需要偏右，即mid 的计算： mid = left+(right-left+1)/2;查找区间右端点模板伪代码如下：

本题还有一个细节：因为数据范围：，所以为了防止溢出，mid 的类型应该为long long;其次是需要处理当x 为0 的边界情况；

参考代码：

    int mySqrt(int x){//处理边界情况if(x == 0) return 0;int left = 1, right = x;while(left < right){long long mid = left + (right-left+1)/2;if(mid*mid <= x) left = mid;else right = mid - 1;}//出了循环left == right ,随便返回一个就可以了return left;  }

题5 山脉数组的峰顶索引：

852. 山脉数组的峰顶索引 - 力扣（LeetCode）

思考：

也就是说这个数组中的数据是先递增然后递减；

解法一：暴力解法

利用指针遍历数据判断当前的数据与下一个数据间的大小关系，遇到第一个当前数据大于下一个数据的时候，当前的下标就是我们所要查找的下标；

接下来我们需要思考的是，我们是否能在暴力解法的基础上进行优化？

显然，数组nums 被天然地分成了两段，即该数据具有二段性，如下：

解法二：二分（利用二段性）

可以将数组分为两段，一段是前面地数据均比当前数据小，一段是前面地数据均比当前数据大；我们的目的是为寻找前面的数据小于当前数据区间的右端点；

那么当 nums[mid-1] < nums[mid] 的时候，left = mid; 当nums[mid-1] > nums[mid] 的时候，right = mid-1; 如果只剩下两个数据，因为我们调整的式子中有 left = mid , 为了避免进入死循环，我们求得的mid 就要偏右，即计算mid ： mid = left + (right-left+1)/2; 同样地，还可以利用小技巧，当出现-1 的时候，计算mid 中就要+1；

其中需要注意的是，要保障 mid -1 ，是合法的，也就是说mid 不可以为0；而数据个数最少是3个，也就是说需要将left 初始化为1，而不是0；

其实此处就是求区间右端点的模板，其伪代码如下：

参考代码：

    int peakIndexInMountainArray(vector<int>& arr) {//数据具有二段性，用二分寻找区间右端点的模板就可以解决int n = arr.size();int left = 1,right = n-1;while(left < right){int mid = left + (right - left +1)/2;if(arr[mid-1] < arr[mid]) left = mid;else// 大于right = mid-1;}//出了循环就意味着 left == rightreturn left;}

题6寻找峰值：

162. 寻找峰
值 - 力扣（LeetCode）

思考：

本题和与上一道题没有什么区别，只不过本题中的数据含有多个峰值，即数据中的趋势呈波浪状；

解法一：暴力解法

从第一个位置开始，一直往后查找，其中需要分情况讨论；

情况一：递减，即直接向下走；那么下标为0的数据就是其中的峰值，可以返回；
情况二：递增，一直在上坡，走到了数据末尾了都还没有下坡，返回最后一个位置就可以了；
情况三：波浪，既有上坡又有下坡，只需要找到开始下坡的位置并返回即可；

解法二：二分，优化暴力解法

我们先抽象一下暴力解法：根据nums[i] 与 nums[i+1] 的特点，我们可以分情况讨论：

（需要注意的是，我们目标的区间要是同一区间，要么是找上升区间的端点要么是找下降区间的端点，此处先分析找下降区间的左端点）

1、nums[i] > nums[i+1] 下降趋势，需要找到下降的这个区间的右端点，这个右端点的左边均是上升趋势，右边是下降趋势；而寻找一个区间的右端点：right = i;
2、nums[i] < nums[i+1] 上升趋势，需要找到下一个下降区间的左端点，这个左端点的左边均是上升趋势，右边均是下降趋势；而寻找一个区间的左端点：left = i+1;

如下图：

因为式子中 right = i , 按道理说为了避免死循环，所求得到的中间点必须要是偏左的，即计算mid: mid = left + (right-left) /2;

参考代码1：

    int findPeakElement(vector<int>& nums) {//寻找下降段的左端点int n = nums.size();int left = 0 , right = n-1;while(left < right){int mid = left + (right - left)/2;if(nums[mid] < nums[mid+1]) left = mid+1;else right = mid;}//出了循环left == rightreturn left;}

同样地，我们还可以找上升区间的右端点：

1、nums[i] > nums[i+1] 下降趋势，right = mid-1;
2、nums[i] < nums[i+1] 上升趋势， left = mid;

求 mid : mid = left + (right - left +1)/2;

参考代码2：

    int findPeakElement(vector<int>& nums) {//寻找上升区间的右端点int n = nums.size();int left = 0 , right = n-1;while(left < right){int mid = left + (right - left +1)/2;if(nums[mid-1] < nums[mid]) left = mid;else  right = mid-1;}return left;}

题7 寻找旋转排序数组中的最小值：

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

思考：

数组原本中的数据是升序的，但是会经过旋转，那么就会有一下两种情况：

解法一：暴力解法

直接遍历寻找最小值

解法二：优化暴力解法

将nums 中数据进行旋转处理之后，会有两种情况，一是维持原状，而是被分成了两截；第一段，是从最前面开始呈现上升趋势，后一段也会呈现上升趋势，由于该数组之中全为不相同的元素，多么明显的二段性，完全可以使用二分来解决；

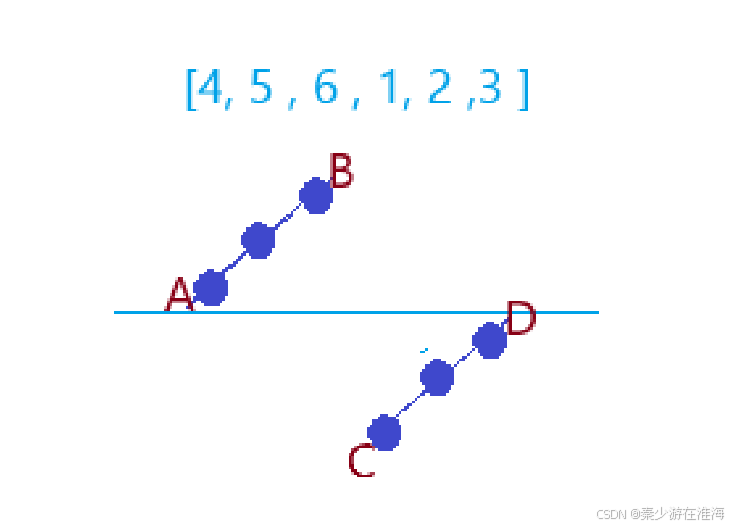
经过观察可以发现，在AB段之中呈现上升趋势，那么A点一定是AB段中最小的值；同理，在CD段中，C点是最小的值；显然地，A点是一定大于C点地，我们只要找到C点就可以了；而C点左边的数据全是大于C中的数据，其右边也全是大于自己的数据，没有数据上的单调性，但是分段是存在的；

Q: 这个时候如何解决呢？

我们将D点中的数据当作参照物，那么大于D点的就是上面的一段，小于D点的就是下面的一段；

假设nums 中的数据个数为n;当nums[i] <= nums[n-1] 就说明 i 下标所对应的数据位于下段；当nums[i] > nums[n-1] 就说明 i 下标所对应的数据位于上段；而我们的目标是求得下段区间的左端点；如下：

Q：我们能否以A点作为判断点？

可以的，但是需要将第二种情况（全递增）进行特殊处理，如下图分析：

参考代码：

    int findMin(vector<int>& nums) {//我们以最后一个数据作为划分段的依据,所以是查找区间的左端点int n = nums.size();int left = 0 ,right = n-1;while(left < right){int mid = left + (right - left)/2;if(nums[mid] > nums[n-1]) left = mid+1;else right = mid;}return nums[left];}

题8 点名：

LCR 173. 点名 - 力扣（LeetCode）

思考：

寻找顺序的缺失的数字，本题很简单；

解法一：直接遍历

直接遍历这个数组，因为此数组中的数据严格递增，我们只需要遍历借助于前后数据差是否为1便可；时间复杂度为O(N)；

参考代码1：

    int takeAttendance(vector<int>& records) {//直接遍历int n = records.size();for(int i = 0;i<n;i++){if(records[i]!=i) return i;}return n;}

解法二：哈希表

借助于（n+1）大小的哈希表去遍历数组，遍历结束后看哪一个哈希表中那个位置上是空的即可；时间复杂度为O(N)；

参考代码2：

    int takeAttendance(vector<int>& records) {//hashint n = records.size();int hash[10001] = {0};for(auto e: records) hash[e]++;for(int i = 0; i < n;i++) if(hash[i]==0) return i;return n;}

解法三：位运算

利用^ （按位异或）；按位异或的特点：相同为0相异为1，那么相同给的元素按位异或就会相互抵消；时间复杂度为O(N)；

参考代码3：

    int takeAttendance(vector<int>& records) {//利用按位异或int n = records.size();int ret = 0;for(int i = 0;i<=n;i++) ret^=i;for(auto e: records) ret^=e;return ret;}

解法四：数学方法：高斯求和方式

即等差数列的求和方式：((首项+末尾)*项数)/2;时间复杂度为O(N)；

参考代码4：

    int takeAttendance(vector<int>& records) {//利用按位异或int n = records.size();int ret = ((0+n)*(n+1))/2;for(auto e: records) ret-=e;return ret;}

解法五：二分

利用数组的二段性；因为数据中缺失了一个数，那么数据就会被分成两段，如下：

我们的目的就是找到B或者C，总得找个依据来划分数组吧？想要将数据划分为两段，似乎也是让B或者C作为判断点，但是我们的目的不就是找它们呢？显然，这个逻辑是不自洽的，那么这个思路也是不对的；

我们需要换个角度继续思考：

如果数据完全从0开始往后顺序，数据与下标是一一对应的，但倘若差一个数据那么数据与下标就会差1；这也是二段性，一段是数据与下标一一对应，一段是数据与下标差1；而我们的目标值为第二段区间的下标左端点，如下：

那么就可以利用二分中寻找一个区间左端点的模板来解决这个问题；当 nums[mid] == mid ， left = mid+1; 当nums[mid] >mid 的时候， right = mid; 为了避免死循环，去所求的的mid 要偏左，故而mid 的计算为： mid = left + (right-left)/2;

参考代码5：

    int takeAttendance(vector<int>& records) {//二分int n = records.size();int left = 0 , right = n;while(left < right){int mid = left + (right - left)/2;if(records[mid] == mid) left = mid+1;else right = mid;}return left;}