[论文品鉴] DeepSeek V3 最新论文 之 MHA、MQA、GQA、MLA
DeepSeek本周三发了篇关于V3的论文【Insights into DeepSeek-V3: Scaling Challenges and Reflections on Hardware for AI Architectures】,算是年初论文【DeepSeek-V3 Technical Report】的姊妹篇;主要讲解了,DeepSeek团队如何通过软硬件相结合的方式,只需要2048块Nvidia H800就可以训练出v3。
下图是V3的基础架构,要想做到透彻理解,所需的知识储备也挺多挺杂的,所以决定通过多篇文章来“品鉴”;

今天介绍MLA,但又不能只说MLA,需要把整个“family 累A”(我超好尬)都介绍一下,也包括 MHA、MQA、GQA。
Self Attention
介绍各种A之前,先说下这一切的起点 self attention,这是LLM如何理解语义的基础,像下面两句话中的“真好吃”肯定就不是同一个意思…

self attention 是通过理解 上下文 的方式来理解语义的,例如当发现 真好吃 的语境中有 恒电饭菜 的时候,就知道这是一个 negative 的评价,而这是通过QKV进行点积运算实现的。

例如对于“真好吃”这个token:
- 首先通过它的
query与其他token的key进行点积运算,得到相似度向量: V = [ Q 3 ∗ K 1 , Q 3 ∗ k 2 , Q 3 ∗ K 3 ] V=[Q_3*K_1, Q_3*k_2,Q_3*K_3] V=[Q3∗K1,Q3∗k2,Q3∗K3] - 把它
归一化为相加为 1 1 1的,百分比代表比重的向量: S o f t m a x ( V ) = [ 0.4 , 0.35 , 0.25 ] Softmax(V)=[0.4,0.35,0.25] Softmax(V)=[0.4,0.35,0.25],相似度越大比重越高 - 生成更新后的token向量: V 3 ′ = 0.4 ∗ V 1 + 0.35 ∗ V 2 + 0.25 ∗ V 3 V3'=0.4*V_1 + 0.35 * V_2 + 0.25*V_3 V3′=0.4∗V1+0.35∗V2+0.25∗V3
而对于整个句子来说,是把每个token的“QKV”向量整合到一起,通过公式 A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q ∗ K T d k ) ∗ V Attention(Q,K,V) = softmax(\frac{Q*K^T}{\sqrt{d_k}})*V Attention(Q,K,V)=softmax(dkQ∗KT)∗V 进行计算:
- K K K 矩阵要转置 K T K^T KT,不然矩阵乘法无法计算
- d k d_k dk代表注意力的维度,也就是"QKV"的维度,例如 512 512 512维度,那么单Head的“QKV”就是 512 512 512的向量,8个Head的“QKV”就是 512 8 = 64 \frac{512}{8}=64 8512=64维的向量,所以维度越大上面 Q ∗ K T Q*K^T Q∗KT越膨胀,所以通过除以 d k \sqrt{d_k} dk进行缩放,稳定训练。
MHA
而通过多个Head进行上述self attention计算的方式就是MHA(Multi-Head Attention)
例如一次性的通过 4 4 4个头针对 真好吃 这个token,生成 4 4 4组“QKV”矩阵,每组 “QKV” 分别计算,最后再将这 4 4 4组的新token整合到一起,就得到了这个token通过4个head运算MHA后的结果。

再通过如下公式进行计算:
A t t e n t i o n = C o n c a t ( A t t e n t i o n ( Q h e a d 1 , K h e a d 1 , V h e a d 1 ) , A t t e n t i o n ( Q h e a d 2 , K h e a d 2 , V h e a d 2 ) , A t t e n t i o n ( Q h e a d 3 , K h e a d 3 , V h e a d 3 ) , A t t e n t i o n ( Q h e a d 4 , K h e a d 4 , V h e a d 4 ) ) Attention=Concat(\\ \qquad Attention(Q_{head1},K_{head1},V_{head1}), \\ \qquad Attention(Q_{head2},K_{head2}, V_{head2}), \\ \qquad Attention(Q_{head3},K_{head3},V_{head3}), \\ \qquad Attention(Q_{head4},K_{head4},V_{head4}) \\) Attention=Concat(Attention(Qhead1,Khead1,Vhead1),Attention(Qhead2,Khead2,Vhead2),Attention(Qhead3,Khead3,Vhead3),Attention(Qhead4,Khead4,Vhead4))
KV Cache
LLM generate的过程,也就是在推理时,是Decoder自递归式的生成下一个token,就是不断的用query乘以之前token的key再结合之前token的value的过程;
例如:对于第一个token,通过 “QKV” 矩阵得到下一个token:

再结合新token,生成下一个token:当前token的query乘以之前token的key和自己的key,然后再结合之前token的value和自己的value

而在整个过程中,之前token的key和value是不变的,不需要再计算了,但是之前token的query却用不到了,所以可以把key和value缓存起来加速运算,这就是KV cache
有了KV cache后,上面的计算过程就简化成了,第二次只需要计算当前token即可:

看起来很不错是吧,但这是用 宝贵的显存 换来的,也就是 空间换时间。
那么有没有进一步减少 显存 占用的方法呢?那就是:MQA 和 GQA
MQA
MQA(Multi Query Attention)它的核心思想是,多头共享KV。
例如,正常情况下,3个Head的MHA,需要cache3组KV:

但在MQA中,只存储1组KV,而保留多头query:

这样可以大大减少KV cache的大小,但却会大大降低实际效果。
GQA
为了折中MHA和MQA,人们设计了GQA(Group Query Attention),它的核心思想是:每组Query共享一份KV cache。

以上MHA、MQA、GQA的对比就可以浓缩成下面整张经典的图:

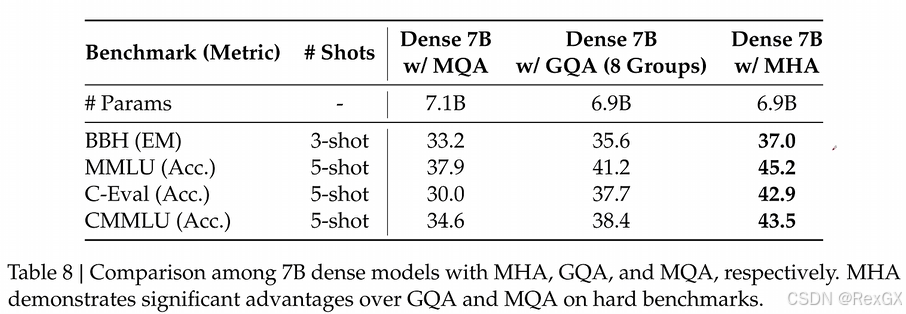
从在DeepSeek提供的数据来看,GQA虽然比MQA好,但和MHA相比,还是会降低模型性能。
那么进一步的,有没有降低KV cache,又能完全保持模型性能,甚至提高模型性能呢?那就是DeepSeek的MLA。
MLA
MLA (Multi-Head Laten Attention)它的核心思想也很简单,就是:矩阵的压缩与解压缩 (有点类似LoRA引入的低秩矩阵,可以看下之前文章)

对于KV:
- 首先通过一个
压缩矩阵进行压缩,可以表示为: W D k v W_{Dkv} WDkv,其中的 D D D表示down压缩 - 然后只需要存储压缩后的
KV - 最后在实际使用时,再通过两个
解压缩矩阵进行解压缩,可以表示为: W U k W_{Uk} WUk和 W U v W_{Uv} WUv,其中的 U U U表示为up解压缩
从DeepSeek提供的数据来看,MLA的实际效果甚至比MHA还要好:

所以MLA既大大降低了KV显存占用,还能提升性能,确实很牛…
但是,MLA引入的 压缩与解压缩 过程,不是会增加计算量么,这和引入 cache 的初衷步不是相背了么?
其实可以通过公式推导发现,MLA并没有实际引入太多的额外计算:
- 先看正常的注意力计算公式: A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q ∗ K T d k ) ∗ V Attention(Q,K,V) = softmax(\frac{Q*K^T}{\sqrt{d_k}})*V Attention(Q,K,V)=softmax(dkQ∗KT)∗V
- 在
MLA中,以K为例,有 K = C K V ∗ W U K K=C^{KV}*W^{UK} K=CKV∗WUK,也就是需要先压缩 C K V C^{KV} CKV,然后再解压缩 W U K W^{UK} WUK - 保持Q不变 Q = W Q Q=W^Q Q=WQ,一起带入之前的公式得到:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q ∗ K T d k ) ∗ V = s o f t m a x ( W Q ( C K V ∗ W U K ) T d k ) ∗ V = s o f t m a x ( W Q ∗ W U K T ∗ C K V T d k ∗ V Attention(Q,K,V) \\ \qquad = softmax(\frac{Q*K^T}{\sqrt{d_k}})*V \\ \qquad = softmax(\frac{W^Q(C^{KV}*W^{UK})^T}{\sqrt{d_k}})*V\\ \qquad = softmax(\frac{W^Q*W^{UK^T}*C^{KV^T}}{\sqrt{d_k}}*V Attention(Q,K,V)=softmax(dkQ∗KT)∗V=softmax(dkWQ(CKV∗WUK)T)∗V=softmax(dkWQ∗WUKT∗CKVT∗V
其中的 W Q ∗ W U K T W^Q*W^{UK^T} WQ∗WUKT可以进行合并,在推理前就计算好,就不需要额外进行 解压 计算了。
同样的,也对query进行类似的 压缩与解压缩 操作,但与kv不同的是,并不需要 存储query的压缩矩阵。

但是经过上述的矩阵集合,会打破 位置编码 信息,所以 DeepSeek 引入了额外的矩阵,去保存位置编码信息,也就是图中的这两部分:

以上从MHA介绍到了MLA,可以看出DeepSeek是如何降低了KV cache,减少了对显存的依赖;下一篇继续介绍 DeepSeek的 MoE 如何通过 稀疏激活 减少 显存占用和计算量。
