当前位置： 首页 > news >正文

深入理解位图（Bit - set）：概念、实现与应用

news 2025/5/19 5:15:04

目录

引言 

一、位图概念 

（一）基本原理 

（二）适用场景 

二、位图的实现（C++ 代码示例） 

 三、位图应用

1. 快速查找某个数据是否在一个集合中

2. 排序 + 去重 

3. 求两个集合的交集、并集等 

4. 操作系统中磁盘块标记 

四、总结 

引言
 

在处理海量数据时，如何高效地存储和查询数据是一个关键问题。位图（Bit - set）作为一种非常巧妙的数据结构，在很多场景下能够极大地提升数据处理的效率。今天，我们就来深入探讨一下位图的相关知识。
 

一、位图概念
 

（一）基本原理
 


位图，简单来说，就是用每一位来存放某种状态。它特别适用于海量数据且数据无重复的场景，通常用于判断某个数据是否存在。比如，给定40亿个不重复的无符号整数，要快速判断一个无符号整数是否在这40亿个数中。数据是否存在刚好是两种状态（存在或不存在），此时就可以使用一个二进制比特位来代表数据是否存在的信息。如果二进制比特位为1，代表存在；为0，则代表不存在。
 
假设我们有一个整数数组  int array[] = {1,3,7,4,12,16,19,13,22,18};  ，我们可以按照一定规则将这些数映射到位图中。例如，将整数的范围划分为若干段，像0 - 7、8 - 15、16 - 23等，每个整数对应位图中的一个比特位。
 

（二）适用场景
 

1. 快速查找：在海量数据集中快速判断某个数据是否存在，相比传统的遍历查找（时间复杂度O(N) ）或者排序后二分查找（时间复杂度O(logN) ），位图在某些情况下可以实现更高效的查找。
2. 数据去重与统计：在统计一些不重复元素的相关信息时，位图可以帮助我们快速标记已经出现过的元素，方便进行去重和统计数量等操作。
 

二、位图的实现（C++ 代码示例）
 


下面是一个简单的位图类  bitset  的C++ 实现代码：

#pragma once
#include<vector>namespace ldg
{template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}// x映射的那个标记成1void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}// x映射的那个标记成0void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _a[i] & (1 << j);}private:vector<int> _a;};template<size_t N>class twobitset{public:void set(size_t x){// 00 -> 01if (!_bs1.test(x) && !_bs2.test(x)){_bs2.set(x);} // 01 -> 10else if (!_bs1.test(x) && _bs2.test(x)){_bs1.set(x);_bs2.reset(x);}// 本身10代表出现2次及以上，就不变了}bool is_once(size_t x){return !_bs1.test(x) && _bs2.test(x);}private:bitset<N> _bs1;bitset<N> _bs2;};
}

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<unordered_set>
#include<unordered_map>
#include<set>
using namespace std;#include"BitSet.h"//int main()
//{
//	bit::bitset<1000> bs;
//	bs.set(1);
//	bs.set(10);
//	bs.set(100);
//
//	cout << bs.test(1) << endl;
//	cout << bs.test(10) << endl;
//	cout << bs.test(100) << endl;
//	cout << bs.test(999) << endl<<endl;
//
//	bs.set(999);
//	bs.reset(10);
//
//	cout << bs.test(1) << endl;
//	cout << bs.test(10) << endl;
//	cout << bs.test(100) << endl;
//	cout << bs.test(999) << endl << endl;
//
//	getchar();
//
//	bit::bitset<-1> bs1;
//	//bit::bitset<0xffffffff> bs2;
//
//	getchar();
//
//	return 0;
//}//int main()
//{
//	int a[] = { 1,2,3,3,4,4,4,4,4,2,3,6,3,1,5,5,8,9};
//	bit::twobitset<10> tbs;
//	for (auto e : a)
//	{
//		tbs.set(e);
//	}
//
//	for (auto e : a)
//	{
//		if (tbs.is_once(e))
//		{
//			cout << e << " ";
//		}
//	}
//	cout << endl;
//}int main()
{int a1[] = { 1,2,3,3,4,4,4,4,4,2,3,6,3,1,5,5,8,9 };int a2[] = { 8,4,8,4,1,1,1,1 };ldg::bitset<10> bs1;ldg::bitset<10> bs2;// 去重for (auto e : a1){bs1.set(e);}// 去重for (auto e : a2){bs2.set(e);}for (int i = 0; i < 10; i++){if (bs1.test(i) && bs2.test(i)){cout << i << " ";}}cout << endl;
}

代码解释
 
1. 构造函数： bitset(size_t bitCount)  根据传入的比特位总数  bitCount  来初始化位图。通过  (bitCount >> 5) + 1  计算出需要的  int  类型数组的大小，因为一个  int  有32位，右移5位（相当于除以32），并加1是为了保证能容纳所有比特位。
2.  set  函数：将指定的比特位  which  置为1。先判断  which  是否越界，然后通过位运算计算出该比特位在  _bit  数组中的索引  index  和在该  int  中的位置  pos  ，最后使用  |=  操作将对应位置置1。
3.  reset  函数：将指定的比特位  which  置为0。同样先判断越界，计算索引和位置后，使用  &=  和按位取反操作将对应位置清零。
4.  test  函数：检测指定比特位  which  是否为1。判断越界后，计算索引和位置，通过与运算判断对应位置是否为1。
5.  size  函数：返回位图中比特位的总个数。
6.  Count  函数：统计位图中为1的比特位的个数。通过一个预先定义好的  bitCnttable  数组来快速统计每个字节中1的个数，遍历  _bit  数组进行累加。
 

 三、位图应用

1. 快速查找某个数据是否在一个集合中

看对应bit位是1是0

#include <vector>
#include <iostream>class bitset {
public:bitset(size_t bitCount) : _bit((bitCount >> 5) + 1), _bitCount(bitCount) {}void set(size_t which) {if (which > _bitCount) return;size_t index = (which >> 5);size_t pos = which % 32;_bit[index] |= (1 << pos);}bool test(size_t which) const {if (which > _bitCount) return false;size_t index = (which >> 5);size_t pos = which % 32;return _bit[index] & (1 << pos);}private:std::vector<int> _bit;size_t _bitCount;
};int main() {// 假设集合元素的范围最大到100bitset setBits(100);// 向集合中添加元素int elements[] = {10, 20, 30, 40};for (int element : elements) {setBits.set(element);}// 查找元素int target = 30;if (setBits.test(target)) {std::cout << target << " is in the set." << std::endl;} else {std::cout << target << " is not in the set." << std::endl;}return 0;
}


 
解释：先创建一个  bitset  对象，指定其大小涵盖集合元素可能的范围。通过  set  函数将集合中的元素对应比特位置1 ，之后使用  test  函数传入要查找的元素，根据返回值判断元素是否在集合中。
 

2. 排序 + 去重
 

#include <vector>
#include <iostream>
#include <algorithm>class bitset {
public:bitset(size_t bitCount) : _bit((bitCount >> 5) + 1), _bitCount(bitCount) {}void set(size_t which) {if (which > _bitCount) return;size_t index = (which >> 5);size_t pos = which % 32;_bit[index] |= (1 << pos);}bool test(size_t which) const {if (which > _bitCount) return false;size_t index = (which >> 5);size_t pos = which % 32;return _bit[index] & (1 << pos);}private:std::vector<int> _bit;size_t _bitCount;
};int main() {// 假设集合元素的范围最大到100bitset setBits(100);// 原始数组，包含重复元素int arr[] = {10, 20, 10, 30, 20, 40};for (int element : arr) {setBits.set(element);}std::vector<int> sortedUnique;for (size_t i = 0; i < setBits.size(); ++i) {if (setBits.test(i)) {sortedUnique.push_back(i);}}std::sort(sortedUnique.begin(), sortedUnique.end());for (int num : sortedUnique) {std::cout << num << " ";}std::cout << std::endl;return 0;
}


 
解释：利用  bitset  ，将数组元素对应比特位置1 ，实现去重。之后遍历  bitset  ，将为1的比特位对应的整数添加到新的  vector  中，最后对这个  vector  进行排序，得到去重且有序的序列。
 

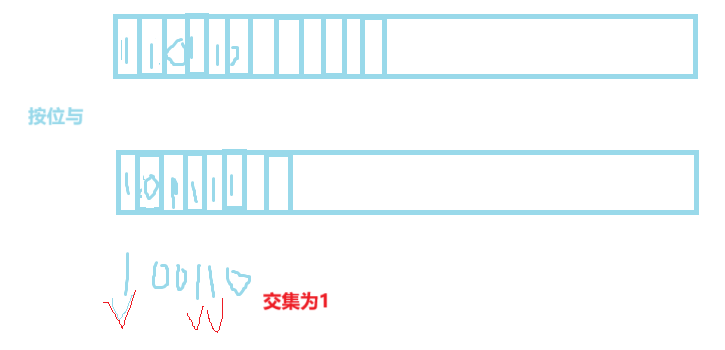
3. 求两个集合的交集、并集等
 

#include <vector>
#include <iostream>class bitset {
public:bitset(size_t bitCount) : _bit((bitCount >> 5) + 1), _bitCount(bitCount) {}void set(size_t which) {if (which > _bitCount) return;size_t index = (which >> 5);size_t pos = which % 32;_bit[index] |= (1 << pos);}bool test(size_t which) const {if (which > _bitCount) return false;size_t index = (which >> 5);size_t pos = which % 32;return _bit[index] & (1 << pos);}bitset intersection(const bitset& other) const {if (_bitCount!= other._bitCount) {std::cerr << "Bitsets must have the same size for intersection." << std::endl;return bitset(0);}bitset result(_bitCount);for (size_t i = 0; i < _bit.size(); ++i) {result._bit[i] = _bit[i] & other._bit[i];}return result;}bitset unionSet(const bitset& other) const {if (_bitCount!= other._bitCount) {std::cerr << "Bitsets must have the same size for union." << std::endl;return bitset(0);}bitset result(_bitCount);for (size_t i = 0; i < _bit.size(); ++i) {result._bit[i] = _bit[i] | other._bit[i];}return result;}private:std::vector<int> _bit;size_t _bitCount;
};int main() {// 假设集合元素的范围最大到100bitset setBits1(100);bitset setBits2(100);int elements1[] = {10, 20, 30};int elements2[] = {20, 30, 40};for (int element : elements1) {setBits1.set(element);}for (int element : elements2) {setBits2.set(element);}bitset intersectionResult = setBits1.intersection(setBits2);bitset unionResult = setBits1.unionSet(setBits2);std::cout << "Intersection: ";for (size_t i = 0; i < intersectionResult.size(); ++i) {if (intersectionResult.test(i)) {std::cout << i << " ";}}std::cout << std::endl;std::cout << "Union: ";for (size_t i = 0; i < unionResult.size(); ++i) {if (unionResult.test(i)) {std::cout << i << " ";}}std::cout << std::endl;return 0;
}


 
解释：先分别创建表示两个集合的  bitset  对象，将集合元素对应比特位置1 。通过  intersection  函数实现按位与操作得到交集位图，通过  unionSet  函数实现按位或操作得到并集位图，最后遍历位图输出交集和并集中的元素。
 

4. 操作系统中磁盘块标记
 

#include <vector>
#include <iostream>class DiskBlockBitset {
public:DiskBlockBitset(size_t blockCount) : _bit((blockCount >> 5) + 1), _blockCount(blockCount) {}void markUsed(size_t blockIndex) {if (blockIndex > _blockCount) return;size_t index = (blockIndex >> 5);size_t pos = blockIndex % 32;_bit[index] |= (1 << pos);}void markFree(size_t blockIndex) {if (blockIndex > _blockCount) return;size_t index = (blockIndex >> 5);size_t pos = blockIndex % 32;_bit[index] &= ~(1 << pos);}bool isBlockUsed(size_t blockIndex) const {if (blockIndex > _blockCount) return false;size_t index = (blockIndex >> 5);size_t pos = blockIndex % 32;return _bit[index] & (1 << pos);}private:std::vector<int> _bit;size_t _blockCount;
};int main() {// 假设磁盘块总数为100DiskBlockBitset diskBlocks(100);// 标记一些磁盘块为已使用int usedBlocks[] = {10, 20, 30};for (int block : usedBlocks) {diskBlocks.markUsed(block);}// 检查某个磁盘块状态int checkBlock = 20;if (diskBlocks.isBlockUsed(checkBlock)) {std::cout << "Disk block " << checkBlock << " is used." << std::endl;} else {std::cout << "Disk block " << checkBlock << " is free." << std::endl;}// 释放一个磁盘块diskBlocks.markFree(20);if (diskBlocks.isBlockUsed(checkBlock)) {std::cout << "Disk block " << checkBlock << " is still used." << std::endl;} else {std::cout << "Disk block " << checkBlock << " is now free." << std::endl;}return 0;
}


 
 
解释：定义  DiskBlockBitset  类模拟操作系统中磁盘块标记。通过  markUsed  函数将指定磁盘块对应比特位置1表示已使用， markFree  函数将对应比特位置0表示空闲， isBlockUsed  函数用于检测磁盘块是否被使用。


 

四、总结
 

位图作为一种高效的数据结构，在处理海量数据的存在性判断、数据统计等方面有着广泛的应用。通过合理利用位图的特性，我们可以在很多场景下优化程序的性能，减少时间和空间复杂度。希望通过这篇博客，大家能对位图有更深入的理解，并在实际编程中灵活运用。

http://www.xdnf.cn/news/508159.html

相关文章：

  • python中http.cookiejar和http.cookie的区别
  • 深入解析Spring Boot与Kafka集成：构建高性能消息驱动应用
  • 【技海登峰】Kafka漫谈系列（十一）SpringBoot整合Kafka之消费者Consumer
  • 【云原生架构反模式】常见误区与解决方案
  • WPS多级标题编号以及样式控制
  • ES（ES2023/ES14）最新更新内容，及如何减少内耗
  • 大模型微调：从基础模型到专用模型的演进之路
  • IDE/IoT/搭建物联网(LiteOS)集成开发环境，基于 LiteOS Studio + GCC + JLink
  • 为新装的Linux系统配置国内yum源（阿里源）
  • 19. 结合Selenium和YAML对页面实例化PO对象改造
  • 大数据场景下数据导出的架构演进与EasyExcel实战方案
  • 理想AI Talk第二季-重点信息总结
  • 【架构美学】Java 访问者模式：解构数据与操作的双重分发哲学
  • 基于单片机路灯自动控制仪仿真设计
  • 包装设备跨系统兼容：Profinet转Modbus TCP的热收缩包装机改造方案
  • 出现 Uncaught ReferenceError: process is not defined 错误
  • 【NLP 75、如何通过API调用智谱大模型】
  • Spring Web MVC————入门(3)
  • ngx_http_rewrite_module 技术指南
  • 2025年、2024年最新版IntelliJ IDEA下载安装过程（含Java环境搭建+Maven下载及配置）
  • 操作系统之EXT文件系统
  • windows笔记本连接RKNN3588网络配置解析
  • Go 与 Gin 搭建简易 Postman：实现基础 HTTP 拨测的详细指南
  • golang选项设计模式
  • Linux518 YUM源仓库回顾（需查）ssh 服务配置回顾 特定任务配置回顾
  • 51单片机，两路倒计时，LCD1602 ，Proteus仿真
  • 逻辑与非逻辑的弥聚
  • C++笔试题(金山科技新未来训练营）：
  • 基于simulink搭建的模块化多电平MMC仿真模型
  • 如何给PSCAD添加库文件