第二十二天打卡
数据预处理
import pandas as pd
from sklearn.model_selection import train_test_splitdef data_preprocessing(file_path):"""泰坦尼克号生存预测数据预处理函数参数:file_path: 原始数据文件路径返回:preprocessed_data: 预处理后的数据集"""# 数据加载与初步查看data = pd.read_csv(file_path)# 缺失值处理age_mean = data['Age'].mean()data['Age'].fillna(age_mean, inplace=True)embarked_mode = data['Embarked'].mode()[0]data['Embarked'].fillna(embarked_mode, inplace=True)data.drop('Cabin', axis=1, inplace=True)# 分类变量编码data = pd.get_dummies(data, columns=['Sex', 'Embarked'], prefix=['Sex', 'Embarked'])# 异常值处理def remove_outliers_IQR(df, column):Q1 = df[column].quantile(0.25)Q3 = df[column].quantile(0.75)IQR = Q3 - Q1lower_bound = Q1 - 1.5 * IQRupper_bound = Q3 + 1.5 * IQRreturn df[(df[column] >= lower_bound) & (df[column] <= upper_bound)]data = remove_outliers_IQR(data, 'Fare')# 删除无用特征useless_columns = ['PassengerId', 'Name', 'Ticket']data.drop(useless_columns, axis=1, inplace=True)return datadef split_dataset(data, test_size=0.2, random_state=42):"""划分预处理后的数据为训练集和测试集参数:data: 预处理后的数据test_size: 测试集占比random_state: 随机种子返回:X_train, X_test, y_train, y_test: 划分后的训练集和测试集"""X = data.drop(['Survived'], axis=1) # 特征,axis=1表示按列删除y = data['Survived'] # 标签X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state) # 划分数据集# 训练集和测试集的形状print(f"训练集形状: {X_train.shape}, 测试集形状: {X_test.shape}") # 打印训练集和测试集的形状return X_train, X_test, y_train, y_test# ====================== 执行预处理和数据集划分 ======================
if __name__ == "__main__":input_file = "train.csv" # 确保文件在当前工作目录preprocessed_data = data_preprocessing(input_file)# 划分数据集X_train, X_test, y_train, y_test = split_dataset(preprocessed_data)# 保存预处理后的数据和划分后的数据集output_file = "train_preprocessed.csv"preprocessed_data.to_csv(output_file, index=False)print(f"\n预处理后数据已保存至:{output_file}")# 保存划分后的数据集(可选)pd.concat([X_train, y_train], axis=1).to_csv("train_split.csv", index=False)pd.concat([X_test, y_test], axis=1).to_csv("test_split.csv", index=False)print(f"训练集已保存至:train_split.csv")print(f"测试集已保存至:test_split.csv")模型
SVM
# SVM
svm_model = SVC(random_state=42)
svm_model.fit(X_train, y_train)
svm_pred = svm_model.predict(X_test)print("\nSVM 分类报告:")
print(classification_report(y_test, svm_pred)) # 打印分类报告
print("SVM 混淆矩阵:")
print(confusion_matrix(y_test, svm_pred)) # 打印混淆矩阵# 计算 SVM 评估指标,这些指标默认计算正类的性能
svm_accuracy = accuracy_score(y_test, svm_pred)
svm_precision = precision_score(y_test, svm_pred)
svm_recall = recall_score(y_test, svm_pred)
svm_f1 = f1_score(y_test, svm_pred)
print("SVM 模型评估指标:")
print(f"准确率: {svm_accuracy:.4f}")
print(f"精确率: {svm_precision:.4f}")
print(f"召回率: {svm_recall:.4f}")
print(f"F1 值: {svm_f1:.4f}")
KNN
# KNN
knn_model = KNeighborsClassifier()
knn_model.fit(X_train, y_train)
knn_pred = knn_model.predict(X_test)print("\nKNN 分类报告:")
print(classification_report(y_test, knn_pred))
print("KNN 混淆矩阵:")
print(confusion_matrix(y_test, knn_pred))knn_accuracy = accuracy_score(y_test, knn_pred)
knn_precision = precision_score(y_test, knn_pred)
knn_recall = recall_score(y_test, knn_pred)
knn_f1 = f1_score(y_test, knn_pred)
print("KNN 模型评估指标:")
print(f"准确率: {knn_accuracy:.4f}")
print(f"精确率: {knn_precision:.4f}")
print(f"召回率: {knn_recall:.4f}")
print(f"F1 值: {knn_f1:.4f}")
逻辑回归
# 逻辑回归
logreg_model = LogisticRegression(random_state=42)
logreg_model.fit(X_train, y_train)
logreg_pred = logreg_model.predict(X_test)print("\n逻辑回归 分类报告:")
print(classification_report(y_test, logreg_pred))
print("逻辑回归 混淆矩阵:")
print(confusion_matrix(y_test, logreg_pred))logreg_accuracy = accuracy_score(y_test, logreg_pred)
logreg_precision = precision_score(y_test, logreg_pred)
logreg_recall = recall_score(y_test, logreg_pred)
logreg_f1 = f1_score(y_test, logreg_pred)
print("逻辑回归 模型评估指标:")
print(f"准确率: {logreg_accuracy:.4f}")
print(f"精确率: {logreg_precision:.4f}")
print(f"召回率: {logreg_recall:.4f}")
print(f"F1 值: {logreg_f1:.4f}")
朴素贝叶斯
# 朴素贝叶斯
nb_model = GaussianNB()
nb_model.fit(X_train, y_train)
nb_pred = nb_model.predict(X_test)print("\n朴素贝叶斯 分类报告:")
print(classification_report(y_test, nb_pred))
print("朴素贝叶斯 混淆矩阵:")
print(confusion_matrix(y_test, nb_pred))nb_accuracy = accuracy_score(y_test, nb_pred)
nb_precision = precision_score(y_test, nb_pred)
nb_recall = recall_score(y_test, nb_pred)
nb_f1 = f1_score(y_test, nb_pred)
print("朴素贝叶斯 模型评估指标:")
print(f"准确率: {nb_accuracy:.4f}")
print(f"精确率: {nb_precision:.4f}")
print(f"召回率: {nb_recall:.4f}")
print(f"F1 值: {nb_f1:.4f}")
决策树
# 决策树
dt_model = DecisionTreeClassifier(random_state=42)
dt_model.fit(X_train, y_train)
dt_pred = dt_model.predict(X_test)print("\n决策树 分类报告:")
print(classification_report(y_test, dt_pred))
print("决策树 混淆矩阵:")
print(confusion_matrix(y_test, dt_pred))dt_accuracy = accuracy_score(y_test, dt_pred)
dt_precision = precision_score(y_test, dt_pred)
dt_recall = recall_score(y_test, dt_pred)
dt_f1 = f1_score(y_test, dt_pred)
print("决策树 模型评估指标:")
print(f"准确率: {dt_accuracy:.4f}")
print(f"精确率: {dt_precision:.4f}")
print(f"召回率: {dt_recall:.4f}")
print(f"F1 值: {dt_f1:.4f}")随机森林
# 随机森林
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train)
rf_pred = rf_model.predict(X_test)print("\n随机森林 分类报告:")
print(classification_report(y_test, rf_pred))
print("随机森林 混淆矩阵:")
print(confusion_matrix(y_test, rf_pred))rf_accuracy = accuracy_score(y_test, rf_pred)
rf_precision = precision_score(y_test, rf_pred)
rf_recall = recall_score(y_test, rf_pred)
rf_f1 = f1_score(y_test, rf_pred)
print("随机森林 模型评估指标:")
print(f"准确率: {rf_accuracy:.4f}")
print(f"精确率: {rf_precision:.4f}")
print(f"召回率: {rf_recall:.4f}") 
网格搜索优化
# --- 2. 网格搜索优化随机森林 ---
print("\n--- 2. 网格搜索优化随机森林 (训练集 -> 测试集) ---")
from sklearn.model_selection import GridSearchCV
import time
# 定义要搜索的参数网格
param_grid = {'n_estimators': [50, 100, 200],'max_depth': [None, 10, 20, 30],'min_samples_split': [2, 5, 10],'min_samples_leaf': [1, 2, 4]
}# 创建网格搜索对象
grid_search = GridSearchCV(estimator=RandomForestClassifier(random_state=42), # 随机森林分类器param_grid=param_grid, # 参数网格cv=5, # 5折交叉验证n_jobs=-1, # 使用所有可用的CPU核心进行并行计算scoring='accuracy') # 使用准确率作为评分标准start_time = time.time()
# 在训练集上进行网格搜索
grid_search.fit(X_train, y_train) # 在训练集上训练,模型实例化和训练的方法都被封装在这个网格搜索对象里了
end_time = time.time()print(f"网格搜索耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", grid_search.best_params_) #best_params_属性返回最佳参数组合# 使用最佳参数的模型进行预测
best_model = grid_search.best_estimator_ # 获取最佳模型
best_pred = best_model.predict(X_test) # 在测试集上进行预测print("\n网格搜索优化后的随机森林 在测试集上的分类报告:")
print(classification_report(y_test, best_pred))
print("网格搜索优化后的随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, best_pred))

贝叶斯优化
print("\n--- 2. 贝叶斯优化随机森林 (训练集 -> 测试集) ---")
from skopt import BayesSearchCV
from skopt.space import Integer
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time# 定义要搜索的参数空间
search_space = {'n_estimators': Integer(50, 200),'max_depth': Integer(10, 30),'min_samples_split': Integer(2, 10),'min_samples_leaf': Integer(1, 4)
}# 创建贝叶斯优化搜索对象
bayes_search = BayesSearchCV(estimator=RandomForestClassifier(random_state=42),search_spaces=search_space,n_iter=32, # 迭代次数,可根据需要调整cv=5, # 5折交叉验证,这个参数是必须的,不能设置为1,否则就是在训练集上做预测了n_jobs=-1,scoring='accuracy'
)start_time = time.time()
# 在训练集上进行贝叶斯优化搜索
bayes_search.fit(X_train, y_train)
end_time = time.time()print(f"贝叶斯优化耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", bayes_search.best_params_)# 使用最佳参数的模型进行预测
best_model = bayes_search.best_estimator_
best_pred = best_model.predict(X_test)print("\n贝叶斯优化后的随机森林 在测试集上的分类报告:")
print(classification_report(y_test, best_pred))
print("贝叶斯优化后的随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, best_pred)) 
粒子群优化算法
import numpy as np # 导入NumPy库,用于处理数组和矩阵运算
import random # 导入random模块,用于生成随机数
import time # 导入time模块,用于计算优化耗时
from sklearn.ensemble import RandomForestClassifier # 导入随机森林分类器
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix # 导入评估指标
# --- 2. 粒子群优化算法优化随机森林 ---
print("\n--- 2. 粒子群优化算法优化随机森林 (训练集 -> 测试集) ---")# 定义适应度函数,本质就是构建了一个函数实现 参数--> 评估指标的映射
def fitness_function(params): n_estimators, max_depth, min_samples_split, min_samples_leaf = params # 序列解包,允许你将一个可迭代对象(如列表、元组、字符串等)中的元素依次赋值给多个变量。model = RandomForestClassifier(n_estimators=int(n_estimators),max_depth=int(max_depth),min_samples_split=int(min_samples_split),min_samples_leaf=int(min_samples_leaf),random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)return accuracy# 粒子群优化算法实现
def pso(num_particles, num_iterations, c1, c2, w, bounds): # 粒子群优化算法核心函数# num_particles:粒子的数量,即算法中用于搜索最优解的个体数量。# num_iterations:迭代次数,算法运行的最大循环次数。# c1:认知学习因子,用于控制粒子向自身历史最佳位置移动的程度。# c2:社会学习因子,用于控制粒子向全局最佳位置移动的程度。# w:惯性权重,控制粒子的惯性,影响粒子在搜索空间中的移动速度和方向。# bounds:超参数的取值范围,是一个包含多个元组的列表,每个元组表示一个超参数的最小值和最大值。num_params = len(bounds) particles = np.array([[random.uniform(bounds[i][0], bounds[i][1]) for i in range(num_params)] for _ inrange(num_particles)])velocities = np.array([[0] * num_params for _ in range(num_particles)])personal_best = particles.copy()personal_best_fitness = np.array([fitness_function(p) for p in particles])global_best_index = np.argmax(personal_best_fitness)global_best = personal_best[global_best_index]global_best_fitness = personal_best_fitness[global_best_index]for _ in range(num_iterations):r1 = np.array([[random.random() for _ in range(num_params)] for _ in range(num_particles)])r2 = np.array([[random.random() for _ in range(num_params)] for _ in range(num_particles)])velocities = w * velocities + c1 * r1 * (personal_best - particles) + c2 * r2 * (global_best - particles)particles = particles + velocitiesfor i in range(num_particles):for j in range(num_params):if particles[i][j] < bounds[j][0]:particles[i][j] = bounds[j][0]elif particles[i][j] > bounds[j][1]:particles[i][j] = bounds[j][1]fitness_values = np.array([fitness_function(p) for p in particles])improved_indices = fitness_values > personal_best_fitnesspersonal_best[improved_indices] = particles[improved_indices]personal_best_fitness[improved_indices] = fitness_values[improved_indices]current_best_index = np.argmax(personal_best_fitness)if personal_best_fitness[current_best_index] > global_best_fitness:global_best = personal_best[current_best_index]global_best_fitness = personal_best_fitness[current_best_index]return global_best, global_best_fitness# 超参数范围
bounds = [(50, 200), (10, 30), (2, 10), (1, 4)] # n_estimators, max_depth, min_samples_split, min_samples_leaf# 粒子群优化算法参数
num_particles = 20
num_iterations = 10
c1 = 1.5
c2 = 1.5
w = 0.5start_time = time.time()
best_params, best_fitness = pso(num_particles, num_iterations, c1, c2, w, bounds)
end_time = time.time()print(f"粒子群优化算法优化耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", {'n_estimators': int(best_params[0]),'max_depth': int(best_params[1]),'min_samples_split': int(best_params[2]),'min_samples_leaf': int(best_params[3])
})# 使用最佳参数的模型进行预测
best_model = RandomForestClassifier(n_estimators=int(best_params[0]),max_depth=int(best_params[1]),min_samples_split=int(best_params[2]),min_samples_leaf=int(best_params[3]),random_state=42)
best_model.fit(X_train, y_train)
best_pred = best_model.predict(X_test)print("\n粒子群优化算法优化后的随机森林 在测试集上的分类报告:")
print(classification_report(y_test, best_pred))
print("粒子群优化算法优化后的随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, best_pred))

XGBOOST
# XGBoost
xgb_model = xgb.XGBClassifier(random_state=42)
xgb_model.fit(X_train, y_train)
xgb_pred = xgb_model.predict(X_test)print("\nXGBoost 分类报告:")
print(classification_report(y_test, xgb_pred))
print("XGBoost 混淆矩阵:")
print(confusion_matrix(y_test, xgb_pred))xgb_accuracy = accuracy_score(y_test, xgb_pred)
xgb_precision = precision_score(y_test, xgb_pred)
xgb_recall = recall_score(y_test, xgb_pred)
xgb_f1 = f1_score(y_test, xgb_pred)
print("XGBoost 模型评估指标:")
print(f"准确率: {xgb_accuracy:.4f}")
print(f"精确率: {xgb_precision:.4f}")
print(f"召回率: {xgb_recall:.4f}")
print(f"F1 值: {xgb_f1:.4f}") 
shape可解释性分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import shap
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False # 解决负号显示问题# 加载数据并预处理
def data_preprocessing(file_path):data = pd.read_csv(file_path)# 缺失值处理data['Age'].fillna(data['Age'].mean(), inplace=True)data['Embarked'].fillna(data['Embarked'].mode()[0], inplace=True)data.drop('Cabin', axis=1, inplace=True)# 分类变量编码data = pd.get_dummies(data, columns=['Sex', 'Embarked'], prefix=['Sex', 'Embarked'])# 删除无用特征useless_columns = ['PassengerId', 'Name', 'Ticket']data.drop(useless_columns, axis=1, inplace=True)return data# 加载数据
data = data_preprocessing("train.csv")# 划分特征和目标变量
X = data.drop('Survived', axis=1)
y = data['Survived']# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 使用粒子群优化后的最佳参数训练模型
best_params = [180, 28, 2, 1] # 示例参数,实际应使用PSO优化结果
model = RandomForestClassifier(n_estimators=int(best_params[0]),max_depth=int(best_params[1]),min_samples_split=int(best_params[2]),min_samples_leaf=int(best_params[3]),random_state=42
)
model.fit(X_train, y_train)# 预测并评估
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.4f}")# --------------------- SHAP可解释性分析 ---------------------
# 1. 初始化SHAP解释器
explainer = shap.TreeExplainer(model)# 2. 计算训练集样本的SHAP值
shap_values = explainer.shap_values(X_train)# --------------------- 全局解释 ---------------------
# 3. 特征重要性摘要图
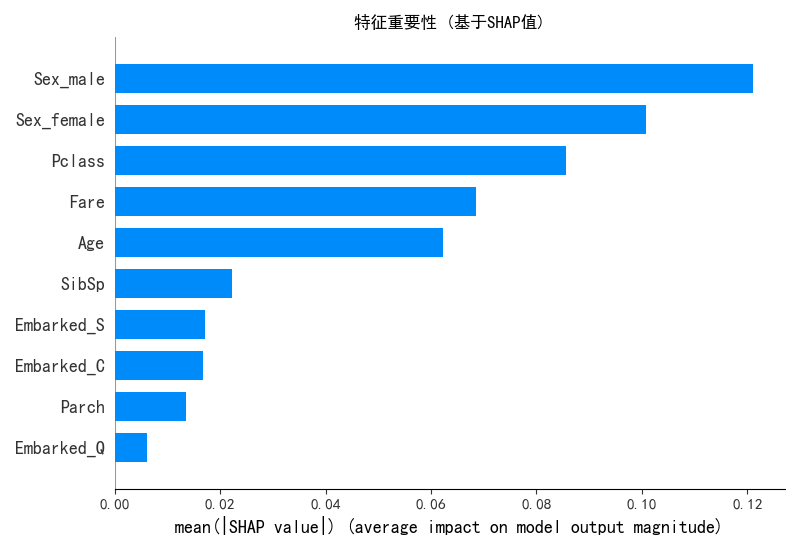
plt.figure(figsize=(10, 6))
shap.summary_plot(shap_values[1], X_train, plot_type="bar", show=False)
plt.title("特征重要性 (基于SHAP值)")
plt.tight_layout()
plt.savefig("shap_feature_importance.png")
plt.close()# 4. 特征影响方向摘要图
plt.figure(figsize=(10, 6))
shap.summary_plot(shap_values[1], X_train, show=False)
plt.title("特征影响方向与强度")
plt.tight_layout()
plt.savefig("shap_summary_plot.png")
plt.close()# 5. 依赖图 - 选择几个最重要的特征进行分析
for feature in X_train.columns:plt.figure(figsize=(10, 6))shap.dependence_plot(feature, shap_values[1], X_train, show=False)plt.tight_layout()plt.savefig(f"shap_dependence_{feature}.png")plt.close()# --------------------- 局部解释 ---------------------
# 6. 选择几个样本进行详细解释
sample_indices = [0, 1, 2, 3] # 选择前4个样本
for idx in sample_indices:plt.figure(figsize=(10, 6))shap.force_plot(explainer.expected_value[1], shap_values[1][idx], X_train.iloc[idx], matplotlib=True,show=False)plt.title(f"样本 {idx} 的SHAP解释 - 预测存活概率: {model.predict_proba(X_train.iloc[[idx]])[0][1]:.4f}")plt.tight_layout()plt.savefig(f"shap_force_plot_{idx}.png")plt.close()# 7. 决策图 - 展示特征如何影响最终决策
for idx in sample_indices:plt.figure(figsize=(12, 6))shap.decision_plot(explainer.expected_value[1], shap_values[1][idx], X_train.iloc[idx],feature_names=list(X_train.columns),show=False)plt.title(f"样本 {idx} 的决策路径")plt.tight_layout()plt.savefig(f"shap_decision_plot_{idx}.png")plt.close()# 8. 保存SHAP值用于后续分析
shap_data = pd.DataFrame(shap_values[1], columns=X_train.columns)
shap_data.to_csv("shap_values.csv", index=False)print("\nSHAP分析完成! 结果已保存为图片文件。")

聚类
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import seaborn as sns# 标准化数据(聚类前通常需要标准化)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 k 值下的指标
k_range = range(2, 11) # 测试 k 从 2 到 10
inertia_values = []
silhouette_scores = []
ch_scores = []
db_scores = []for k in k_range:kmeans = KMeans(n_clusters=k, random_state=42)kmeans_labels = kmeans.fit_predict(X_scaled)inertia_values.append(kmeans.inertia_) # 惯性(肘部法则)silhouette = silhouette_score(X_scaled, kmeans_labels) # 轮廓系数silhouette_scores.append(silhouette)ch = calinski_harabasz_score(X_scaled, kmeans_labels) # CH 指数ch_scores.append(ch)db = davies_bouldin_score(X_scaled, kmeans_labels) # DB 指数db_scores.append(db)print(f"k={k}, 惯性: {kmeans.inertia_:.2f}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 10))# 肘部法则图(Inertia)
plt.subplot(2, 2, 1)
plt.plot(k_range, inertia_values, marker='o')
plt.title('肘部法则确定最优聚类数 k(惯性,越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('惯性')
plt.grid(True)# 轮廓系数图
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='orange')
plt.title('轮廓系数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k(越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()
# 提示用户选择 k 值
selected_k = 5# 使用选择的 k 值进行 KMeans 聚类
kmeans = KMeans(n_clusters=selected_k, random_state=42)
kmeans_labels = kmeans.fit_predict(X_scaled)
X['KMeans_Cluster'] = kmeans_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# KMeans 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=kmeans_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={selected_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 KMeans 聚类标签的前几行
print(f"KMeans Cluster labels (k={selected_k}) added to X:")
print(X[['KMeans_Cluster']].value_counts()) 
import numpy as np
import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 eps 和 min_samples 下的指标
# eps这个参数表示邻域的半径,min_samples表示一个点被认为是核心点所需的最小样本数。
# min_samples这个参数表示一个核心点所需的最小样本数。eps_range = np.arange(0.3, 0.8, 0.1) # 测试 eps 从 0.3 到 0.7
min_samples_range = range(3, 8) # 测试 min_samples 从 3 到 7
results = []for eps in eps_range:for min_samples in min_samples_range:dbscan = DBSCAN(eps=eps, min_samples=min_samples)dbscan_labels = dbscan.fit_predict(X_scaled)# 计算簇的数量(排除噪声点 -1)n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)# 计算噪声点数量n_noise = list(dbscan_labels).count(-1)# 只有当簇数量大于 1 且有有效簇时才计算评估指标if n_clusters > 1:# 排除噪声点后计算评估指标mask = dbscan_labels != -1if mask.sum() > 0: # 确保有非噪声点silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask])ch = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask])db = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask])results.append({'eps': eps,'min_samples': min_samples,'n_clusters': n_clusters,'n_noise': n_noise,'silhouette': silhouette,'ch_score': ch,'db_score': db})print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")else:print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)# 绘制评估指标图,增加点论文中的工作量
plt.figure(figsize=(15, 10))
# 轮廓系数图
plt.subplot(2, 2, 1)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples] # plt.plot(subset['eps'], subset['silhouette'], marker='o', label=f'min_samples={min_samples}')
plt.title('轮廓系数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('轮廓系数')
plt.legend()
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 2)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['ch_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Calinski-Harabasz 指数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('CH 指数')
plt.legend()
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 3)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['db_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Davies-Bouldin 指数确定最优参数(越小越好)')
plt.xlabel('eps')
plt.ylabel('DB 指数')
plt.legend()
plt.grid(True)# 簇数量图
plt.subplot(2, 2, 4)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['n_clusters'], marker='o', label=f'min_samples={min_samples}')
plt.title('簇数量变化')
plt.xlabel('eps')
plt.ylabel('簇数量')
plt.legend()
plt.grid(True)plt.tight_layout()
plt.show()
# 选择 eps 和 min_samples 值(根据图表选择最佳参数)
selected_eps = 0.4 # 根据图表调整
selected_min_samples = 7 # 根据图表调整# 使用选择的参数进行 DBSCAN 聚类
dbscan = DBSCAN(eps=selected_eps, min_samples=selected_min_samples)
dbscan_labels = dbscan.fit_predict(X_scaled)
X['DBSCAN_Cluster'] = dbscan_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# DBSCAN 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=dbscan_labels, palette='viridis')
plt.title(f'DBSCAN Clustering with eps={selected_eps}, min_samples={selected_min_samples} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 DBSCAN 聚类标签的分布
print(f"DBSCAN Cluster labels (eps={selected_eps}, min_samples={selected_min_samples}) added to X:")
print(X[['DBSCAN_Cluster']].value_counts()) 
@浙大疏锦行
