【论文阅读27】-TCN–BiLSTM -滑坡预测

《A Landslide Displacement Prediction Model Based on the ICEEMDAN Method and the TCN–BiLSTM Combined Neural Network》

发表于 Water 期刊，2023年。

---

📌 主要内容概述

这篇论文提出了一种滑坡位移预测模型，结合了：

• ICEEMDAN（改进完全集合经验模态分解与自适应噪声法）用于将滑坡累计位移序列分解为：

  • 趋势项（由滑坡内部地质条件决定）
  • 波动项（由降雨、地下水位等外界因素驱动）

• TCN–BiLSTM 组合神经网络

  • TCN（时序卷积网络）提取特征
  • BiLSTM（双向长短期记忆网络）捕捉特征间的时序关系
  • 结合两者，提升对滑坡位移波动项预测的精度，尤其是复杂非线性时序数据。

---

📌 核心方法流程

1. 数据分解：

   • 用 ICEEMDAN 将滑坡位移数据分解成多个 IMF 和残差项。
   • 残差项作为趋势项，其余 IMF 叠加成波动项。

2. 趋势项预测：

   • 采用三次多项式拟合，预测趋势项未来走势。

3. 波动项预测：

   • 通过灰色关联度（GRG）和最大信息系数（MIC）筛选主要影响因子：

     • 前几天的位移、降雨量、地下水位及其变化

   • 使用 TCN 提取高维特征，输入 BiLSTM 网络进行时序预测。

4. 预测值重构：

   • 将趋势项和波动项预测值相加，得到总位移预测值。

5. 效果验证：

   • 对比了 LSTM、BiLSTM、TCN、TCN–LSTM 和 TCN–BiLSTM 等5个模型，结果显示：

     • TCN–BiLSTM 综合性能最佳，MAPE 仅 0.002，R² 高达 0.999。

---

📌 应用案例

• 研究对象：四川通江县万家湾滑坡

• 监测内容：

  • 地表位移、降雨、地下水位（65个时段）
  • 发现降雨和地下水位是主要触发因素，滑坡位移存在显著滞后性。

---

📌 结论

• ICEEMDAN 分解方法 能有效提高数据物理意义和预测准确性。
• TCN–BiLSTM 组合模型 在处理滑坡非线性波动位移预测时表现优异，适合用于滑坡预警、工程建设安全管理。
• 后续建议：关注模型复杂度和计算资源消耗，合理筛选输入特征以优化效率。

---

全文翻译

摘要
受原生地质条件和外部环境变化的影响，滑坡演化多为非线性演化。针对传统递归神经网络在位移波动型滑坡预测中的不足，提出了一种结合时间卷积神经网络(TCN)和双向长短期记忆神经网络(BiLSTM)的组合神经网络预测模型。基于时间序列分解的思想，采用改进的带自适应噪声的全系综经验模态分解(ICEEMDAN)方法，将位移时间序列数据分解为趋势项和波动项。趋势位移主要受滑坡内部地质条件的影响，采用多项式拟合确定未来趋势位移;波动项的位移主要受滑坡外部环境的影响。本文选取降雨、地下水位高程、滑坡历史位移三种类型的滑坡影响因素。它使用灰色关联(GRG)和互信息(MIC)关联模块的组合进行特征筛选。然后利用TCN提取滑坡特征因子，BiLSTM捕捉特征与位移之间的关系，实现对波项位移的预测。最后，对趋势项和波动项位移预测值进行重构，得到总位移预测值。结果表明，本文提出的ICEEMDAN-TCN-BiLSTM模型能够准确预测滑坡位移，具有较高的工程应用价值，有助于滑坡防灾工程的规划和建设。

关键词* 滑坡位移预测;时间分解;神经网络;地质灾害

1. 简介

山体滑坡作为世界上发生最频繁、分布最广泛、破坏性最强的地质灾害之一，对附近居民的安全、生命和财产造成了重大影响[1-5]。据统计，每年山体滑坡造成4500人死亡，每年山体滑坡造成的经济损失可高达200亿美元[6]。可引发滑坡的因素包括降雨[7-12]、地下水位变化[13-16]、地震[17-19]、人类工程活动[20,21]等，这些因素都有可能引发滑坡等地质灾害。因此，分析和考虑滑坡的影响因素，建立高精度的滑坡位移预测模型，对于准确把握滑坡演化阶段，减少滑坡灾害损失具有重要意义[22,23]。

滑坡累积位移由随时间变化的趋势项位移和由外部因素[24]引起的位移波动项组成。将滑坡累积位移分解为具有实际物理意义的分量，分别建立预测模型，可有效预测滑坡的累积位移。Du et al.[25]将滑坡累积位移分解为趋势项和波动项，并使用BP神经网络预测位移分量。Yang等人[26]使用移动平均法分离滑坡累积位移，并使用支持向量机(SVM)预测周期项位移。Liu et al.[27]使用聚类分析(K-means)表征了滑坡的外部位移和内部状态，并使用支持向量机(SVM)和长短期记忆神经网络(LSTM)预测了滑坡位移。Zhang等人[28]采用变分模态分解(VMD)将监测值分解为高频、中频和低频分量，并构建深度双向长短期记忆神经网络(BiLSTM)分别预测位移分量。Zhang等人[29]采用完整集合经验模态分解(complete ensemble empirical mode decomposition, CEEMD)对累积位移观测值进行分解，并通过多群智能算法(multi-swarm intelligence algorithms, MSI)对SVR模型进行优化，实现滑坡位移预测。

上述方法都取得了不错的效果，但也有各自的不足。在位移时间序列分解方面，移动平均法操作简单，但只能提取位移的趋势项，无法获得滑坡位移的波动项部分。K-means方法对时间序列数据进行分解重构，重构后的数据不具有实际的物理意义。VMD方法可以自由选择位移分量的个数，但对初始条件的依赖性高，计算复杂。CEEMD方法在分解时间数据时存在模态混叠和残留白噪声的问题[30,31]。针对这些问题，ICEEMDAN[32]方法减少了伪模态的数量和残余白噪声的影响。与CEEMD方法相比，该方法还具有较小重构误差少、计算收敛速度快等优点，被广泛应用于生物医学工程和计算机科学等领域[0]。因此，本文采用ICEEMDAN方法对滑坡位移进行分解，提高数据分解质量，使分解项更具物理意义。

预测滑坡位移依赖于预测模型的发展。目前使用的预测模型主要可分为静态模型和动态模型[34-36]。常用的静态模型包括支持向量机回归模型(SVR)和极限学习机模型(ELM)。由于山体滑坡的位移行为主要由外部条件的变化引起，静态模型往往难以考虑山体滑坡复杂的演化过程，无法有效提取历史序列数据[37]。动态模型考虑了时间序列数据的历史特征，如Yang等人[38]和Zhang等人[39]使用LSTM神经网络预测滑坡周期项的位移，其预测效果优于静态模型SVM。Zhang等[40,41]利用门控循环单元(gated recurrent unit, GRU)动态模型挖掘时间数据中的有效历史特征，实现了滑坡位移波动段的准确预测。传统的动态模型虽然已经实现了滑坡时间位移的动态预测，但由于滑坡灾害的突发性和破坏性以及监测样本数据的局限性，其预测精度受到限制。LSTM神经网络需要大量的训练数据，这会导致计算成本增加，模型泛化能力差。然而，GRU神经网络的计算效率优于LSTM神经网络，但其简化的门控结构不能更好地保留和传输信息。Lin等[36]采用双向长短期记忆神经网络(bidirectional long - short memory neural network, BiLSTM)同时考虑影响滑坡位移的历史和未来因素，有效预测了白水河滑坡的位移。由于其独特的双向处理结构，BiLSTM神经网络通常可以提供更丰富的特征表示，这意味着它可以学习与传统的LSTM和GRU相比，预测精度得到了进一步提高。

近年来，时间卷积网络(temporal convolutional network, TCN)神经网络在气象数据预测、计算机数据挖掘等领域得到了广泛的应用。例如，P. Hewage等人将TCN应用于气象预报，实现了对未来天气的长期预测。Fan等人[43]提出了一种基于TCN神经网络的PSTA-TCN框架，通过并行计算显著缩短了模型的训练时间，同时显著提高了准确率。TCN具有扩展的因果卷积结构和出色的特征提取能力，可以挖掘多维特征时间信息。目前，BiLSTM-TCN组合模型很少用于各种社区，几乎从未应用于滑坡灾害。滑坡灾害由于其突发性和季节性，往往表现出非线性位移曲线。预测模型的特征提取和学习能力对于准确预测滑坡位移至关重要。

本文将BiLSTM与TCN相结合，应用于非线性时间位移的预测。通过TCN提取特征变量，并将其输入到时间序列网络BiLSTM中，大大提高了时间序列网络中记忆单元的处理效率，从而减少了训练时间，获得了更准确的预测结果。

本文以万家湾滑坡为研究区域。采用ICEEMDAN分解方法，将滑坡位移监测值分解为具有实际物理意义的趋势项和波动项。拟合多项式得到趋势项位移预测公式，用于预测趋势项位移。采用GRG灰色关联和MIC互信息值的双指标筛选方法，对位移分量、降雨量和地下水位三个候选影响因素进行筛选，得到相关性最大的影响因素。然后，将选取的影响因素作为BiLSTM-TCN组合模型的输入，对模型进行超参数优化训练，用于滑坡波动位移预测。最后，将趋势项的预测位移与波动项的预测位移叠加，得到滑坡的累积位移预测值，并对其进行验证和分析。滑坡位移预测流程图如图1所示。

图1 滑坡位移预测流程图:(a)数据处理，(b)位移预测，(c）模型验证。

2. 方法

2.1. 经验模态分解

EMD在信号处理、振动分析等领域有着广泛的应用。其本质是将非平稳信号数据分解成一系列具有不同特征尺度的序列。分解后的序列称为内禀模态函数(IMF)， IMF的不同内禀模态分量表示不同的特征波动序列。具体分解过程如下[44,45]。

1. 标记监测数据x(t)中的极值点，并将局部最大值点和局部最小值点分别连接起来，形成上下包络曲线，其中m1(t)为上下包络线之间的均值曲线。

2. 进行第一次筛选，第一分量C1(t)的计算公式如下:

在第二次筛选过程中，C1(t)被认为是原始数据，m2(t)是上下包络线之间的平均曲线。重复上述步骤，即可得到分量C2(t)。

3. 重复上述筛选过程，直到Cn(t)为内禀模态函数或残差分量rn(t)变为单调函数，分解过程终止。

4. 分解后的IMF项与rn(t)项之和即为原序列，x(t)公式如下:
   

2.2. 改进的全系综经验模态分解与自适应噪声

CEEMDAN通过加入高斯白噪声解决了EEMD模式混叠和残余噪声问题。ICEEMDAN与CEEMDAN不同，后者在分解过程中直接加入高斯白噪声。而是选取EMD分解后的白噪声的第k个IMF分量，即噪声Ek(ω(i))。以下是ICEEMDAN[30]的一般步骤。

1. 将噪声E1(ω(i))加到原始信号x上，得到:

式中，β0为噪声标准差;ω(i)为加高斯白噪声。

2. 计算第一个模态分量的IMF值:

式中，r1表示一阶残差;c ~ 1为第一模态分量IMF值。

3. 计算第二个模态分量的IMF值:

式中，r2表示二阶残差;c ~ 2为第二模态分量IMF值。

4. 以此类推，计算第k个模态分量的IMF值:

式中，rk表示k阶残差;c ~ k是第k个模态分量的IMF值。

2.3. Temporal Convolutional Network

TCN是一种卷积神经网络，旨在解决递归神经网络中的常见缺陷。它通常用于挖掘图像信息和预测序列数据。TCN结构比典型递归网络更简单清晰，主要由因果卷积核和残差模块[46]组成。

2.3.1. Causal Dilated Convolutional

因果卷积可以理解为时间数据的单向传输。与传统的卷积神经网络不同，在因果卷积中，未来的数据不能影响过去，只在当前和之前的时间步长执行卷积操作。因此，它被称为因果卷积[47]。

如图2所示，在基于因果卷积的卷积过程中，允许对输入进行区间采样。如果d = 1，则表示对每个数据点进行采样;如果d = 2，则表示每两个数据点采样一次。类似地，卷积网络可以得到

即使在更少的卷积层中，也能获得更大的接受场。式(7)是因果扩张卷积[43]的数学表达式:

**图2。**因果展开卷积结构图。

式中，yh,t表示时间t时网络中h层的序列值，fi表示滤波器，k表示卷积核的大小，d表示卷积展开率。

2.3.2. 残差块

残差模块是训练深度网络的一种有价值的技术，因为它允许在层之间发送信息，这有助于防止深度网络训练期间梯度消失或破裂[48,49]。如图3所示，本文构建了一个残差块来代替卷积层。两层非线性映射和卷积构成了一个残差块。

**图3。**残块结构图。

2.4. BiLSTM

LSTM是一种改进的递归神经网络，它引入了一种称为“门”的内部机制，通过学习重要信息和遗忘次要信息来调节信息流，从而更好地处理序列中的长期依赖关系。与标准LSTM不同，BiLSTM同时运行两个独立的LSTM网络，一个处理前端输入序列，另一个处理后端输入序列，如图4所示。这使得网络能够捕获每个时间步之前和之后的信息，包括过去和未来的信息。

2.5. TCN-BiLSTM

由于采用了扩展的因果卷积结构，TCN具有出色的特征提取能力。因此，TCN可以融合原始特征获得更高维度的抽象特征，从而加强对特征信息的挖掘。BiLSTM网络具有较强的时间预测能力。通过结合TCN和BiLSTM网络，

将TCN特征提取并输入到BiLSTM网络中，提高了BiLSTM网络记忆单元的计算性能，使预测模型更有效地学习时间序列的复杂交互关系。因此，本文构建了TCN-BiLSTM预测模型，组合模型结构如图5所示。

**图4。**BiLSTM神经网络结构图。

**图5。**TCN-BiLSTM组合模型结构图。

2.6. 评价指标

本文选取滑坡位移预测中常用的均方根误差(root mean square error, RMSE)、决定系数(coefficient of determination, R2)和平均绝对百分比误差(mean absolute percentage error, MAPE)等技术，对模型的准确性和适用性进行评价。以下是测量指标的计算公式:

公式中，yk为第k个真值样本，yk为第k个预测值样本，yk为所有真值的算术平均值。根据RMSE、MAPE、R2的计算结果进行评价，三者的计算结果均在0 ~ 1的范围内。

3. 研究区概览

3.1. 概述

万家湾滑坡位于四川省通江县北部兴隆镇安平村。它位于通江县北部，大同江西侧，小同江东侧。地形起伏较大，总体呈东北高、西南低的趋势。坡度方向228◦左右，地形坡度一般为10-20◦。滑坡后缘左侧与工程场地平整区相邻，滑坡坡脚位于生活营地内，如图6所示。

**图6。**万家湾滑坡:(a)滑坡边界及监测点布置图;(b) II-II段地质剖面图。

滑坡整体高程在840 ~ 890 m之间，整个滑坡区宽度约222 m。整体平面形状呈“圆椅”状。滑坡纵向长度约为275 m，面积约为3.84 ×104 m2。含碎石的粉质粘土构成了滑坡体的大部分，砾石则主要由砂岩块组成。滑坡体积在38.4 ×104 m3左右，滑坡体平均厚度在10 m左右。滑动带为软塑性粉砂质粘土期含少量角砾岩，透水性差，可形成相对不透水层。滑层为下伏基岩，主要由强至中度风化的碳质砂质泥岩和砂岩组成。

3.2. 宏观变形特征

万家湾滑坡属浅层滑坡，规模为中型滑坡。由于地表土层暴露，加之长期降雨的综合作用，最终发生了滑坡灾害。2022年7月7日，井台北侧上层居住区出现裂缝(图7a)，裂缝最大宽度为20 mm，裂缝最大长度为500 mm。2022年7月19 - 27日在坡脚区进行开挖施工，期间发生两次降雨事件。现场现有裂缝扩大，后缘工程现场平坦区域出现新的裂缝(图7b)。从2022年8月7日开始，在滑坡区设置位移监测点和地下水位监测点。监测期间，既有裂缝不断加剧，新的裂缝不断出现(图7c)。2022年8月7日至28日，除滑坡中心找平区外，位移和变形相对稳定，整体变化较小，而充填区变形较大。2022年8月30-31日连续两天降雨后，发生在居民区的地表沉降裂缝整体变形(图7d)明显加剧。综合分析，滑坡已处于蠕变变形阶段，雨后有加剧的趋势。

图7。滑坡裂缝发育照片:(a)滑坡后缘裂缝，(b)工程场地平坦区域裂缝，©滑坡中部裂缝，(d)台阶裂缝。

3.3. 监测数据及触发因素分析

影响滑坡的因素往往非常复杂，根据其来源可分为内部因素和外部因素[50-52]。不利的环境地质条件，包括斜坡地貌、厚而松散的土层、高度风化的岩性、工程开挖形成的大规模自由面等，是滑坡[53]发生发展的主要内部因素。在内部因素的影响下，滑坡的时间位移关系曲线呈现近似单调函数，反映了滑坡整体累积位移的趋势项。外部因素不同于静态因素，主要是滑坡外部的动态环境因素，包括自然降雨、地下水位、风荷载、环境温湿度等。在外界因素的影响下，滑坡的时间位移关系曲线呈现出一定的波动规律。

本工程采用多种监测方法，获得的监测数据主要包括降雨量、地下水位、地表位移、深部土体位移等。以上数据均来源于现场工程监测报告。对各监测点的数据进行处理分析后，位于滑坡中下部的地表位移监测点D1、D18、J12在整个监测周期内均呈现明显的位移发展趋势。选取上述3个地表位移监测数据和位于滑坡中段的地下水位监测点数据进行研究。所有监测数据包括65个时间段(从2022年8月7日到2022年10月10日)，如图8所示。

图8。万家湾滑坡累积位移、降雨量、地下水位监测资料。

监测期为夏季降雨频繁期，地下水位波动频繁。8月初和8月底发生了两次暴雨事件，导致地下水位急剧上升，期间各监测点的累计位移明显增加。非降雨期，地下水位呈缓慢下降趋势，累计位移增速放缓。8月份的两次暴雨打破了万家湾边坡原有的稳定状态，边坡的整体安全储备大大减少。9、10月连续降雨下，累积位移增长趋势变大，且地下水位上升后累积位移明显增大。在监测周期内，几乎所有的位移加速阶段都发生在降雨事件之后和地下水位波动期间，说明地下水位与降雨量的变化具有一定的

对滑坡变形影响显著。在降雨的作用下，雨水沿着地表裂缝向下渗透到相对不透水的滑动带界面，底部的软质、塑性、粉状粘土被浸透软化，导致滑动带的物理机械强度不断下降。同时，随着土壤含水率的增加，滑动体的重力也随之增大。当滑动力超过抗滑动力时，土壤就会发生滑动。因此，滑坡位移的加速阶段往往发生在降雨事件之后。随着降雨事件的持续，地下水得到大气降雨的补充，导致水位急剧上升。边坡内部的应力场和渗流场在短时间内发生显著变化，从而加速滑坡事件的发生。因此，地下水位的波动也会导致滑坡的加速发生。

4. 结果

4.1. 数据分解

通过对所有监测数据的处理和分析，位于滑坡中心区域的D1监测点数据呈现出明显的位移趋势。由于此时监测数据的完整性较好，因此本文利用该位移序列建立了万家湾滑坡预测模型。我们选取了2022年8月7日至2022年9月27日的52个监测数据集作为训练样本。测试样本为以下13个数据集，时间为2022年9月28日至2022年10月10日。本工作在MATLAB 2022a环境下开发了ICEEMDAN算法，并利用该算法对所选位移序列样本进行解构，如式(3)-(6)所示。该过程的参数设置如下:200次迭代为最大值，标准差比为0.15。

分解后的数据如图9所示。将原始位移序列样本划分为4组位移序列分量，其中IMF1分量波动频率最高，其次是IMF2和IMF3分量，剩余分量R相对平稳，几乎没有波动。因此，残差分量R作为趋势项位移，波动显著的分量IMF1-IMF3之和作为波动项位移。合并后的数据如图10所示。

图9。滑坡总位移ICEEMDAN分解项:(a) IMF1， (b) IMF2， © IMF3， (d) R。

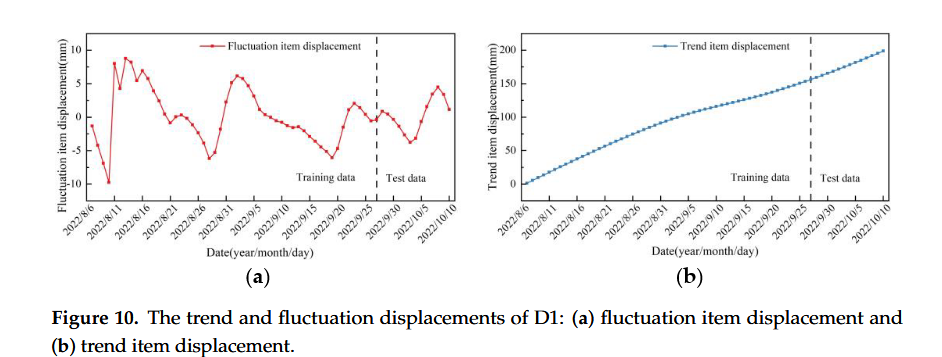
图10。D1的趋势和波动位移:(a)波动项位移和(b)趋势项位移。

4.2. 确定影响因素

影响因素的合理选择决定了预测模型准确率的上限[54-56]。Du等人[57]的研究表明，滑坡过去的状态可以在一定程度上影响滑坡的发展趋势。因此，本文将位移监测值作为滑坡的影响因素之一。在研究河岸边坡时，降雨和水库水位往往被认为是影响滑坡位移的主要因素[58,59]。本文的研究区域位于大同河与晓通河之间，滑坡区离河面较远。因此，未考虑水库水位对滑坡的影响。根据现有的工程监测资料并仔细考虑，降雨、地下水位和历史位移是万家湾滑坡的主要影响因素。

图11为地下水位、日降雨量与波动项位移之间的关系。从图中可以观察到，在降雨频繁的时期，滑坡区内波动项的位移变化明显。在无小雨或有小雨的天气环境中，波动项的位移变化相对平稳。考虑到历史降雨对滑坡未来状态的影响较大，本文将当日、前一日、两天的累积降雨量作为影响滑坡位移的关键因素(输入4-6)。进一步，滑坡区地下水位变化与降雨量之间存在正相关关系，且波动项的位移在地下水位上升时呈现快速增大的趋势。当地下水位略有变化或保持在一定范围内时，波动项的位移变化较小。且波动项的位移往往发生在地下水位上升之后，且地下水位变化对波动项位移的影响具有滞后效应。因此，本文将当日地下水位高程值、前一日及后地下水位变化、与前一日相比地下水位变化减少(输入7-10)作为波动项位移的关键影响因素。最后，本文以前一天的位移、前两天的位移和前一天的累计位移作为波动项位移的影响参数(输入1-3)。

根据上述分析结果，本文初步选取了10个可能的候选因素，如表1所示。图12显示了各因素之间的GRG和MIC值。灰色关联度分析结果表明，降雨和地下水位对波动项位移的影响较大。相比之下，历史位移因子对波动项位移的影响相对较小。最大信息系数分析结果表明，过去一天的位移、每日地下水位高程、与前一天相比地下水位变化减少量与波动项的位移相关性较低。另一个候选项因子项与波动项的位移有较好的相关性;其中，前一天累计位移与波动项位移高度相关。为保证预测结果的准确性，本文选取满足GRG值大于0.80、MIC值大于0.25条件的候选因子作为预测模型的主要影响因子。因此，本文排除了输入1、输入7和输入10三个候选因素，并将其余7个因素确定为影响滑坡波动项位移的关键因素。

图11。地下水位、日降雨量与波动项位移变化的关系。

表1。候选因素。

图12。影响因素的相关分析:(a) GRG和(b) MIC。

4.3. 位移预测

4.3.1. 趋势项目位移预测

趋势项位移使用多项式回归方程进行拟合。为了尽可能保证数据的预测精度，避免使用高阶多项式进行过拟合，本文进行了多次实验分析，最终确定使用三次多项式对数据进行拟合。拟合公式如下，拟合优度R2为0.999，说明拟合效果极佳。

式中，y表示趋势项的位移，x表示时间。

上述方程作为预测模型中趋势项的预测公式，图13显示了趋势项的位移预测结果。MAPE为0.002,RMSE为0.425,R2为0.999。评价指标的计算结果表明，采用三次多项式拟合方法进行趋势位移预测可以取得较好的预测效果。

图13。趋势项目位移预测结果。

4.3.2. 波动项位移预测

在TCN模型中，扩展因子设为4，卷积核大小设为3，隐藏层数设为4。LSTM和BiLSTM模型的隐层神经元取64个。在训练过程中，输入特征是经过相关滤波后最相关的7个特征，将前5组历史数据作为模型预测未来两组数据的输入项。该模型采用贝叶斯优化算法进行超参数优化。组合模型也遵循单个模型的参数设置。

图14显示了不同神经网络的预测结果。LSTM神经网络对波动项位移的预测效果最差，TCN神经网络次之，BiLSTM神经网络次之。根据预测结果计算的预测误差如表2所示。具体分析如下:

1. 由于工程项目提供的滑坡监测数据有限，训练后的LSTM模型泛化性能较差，导致R2为0.915，预测性能不理想。

2. 由于其独特的双向处理结构，BiLSTM神经网络通常提供更丰富的特征表示，这意味着它们可以更好地捕获输入序列中的模式和关系。从总体误差分布来看，BiLSTM的预测误差略低于LSTM的预测误差。最终计算结果LSTM神经网络的预测结果R2为0.945，预测效果优于LSTM。

3. 由卷积神经网络进化而来的TCN比LSTM需要更少的参数，使其更容易训练和调整。因此，即使在有限的训练数据支持下，TCN神经网络也可以实现更准确的位移预测。最终TCN神经网络R2计算结果为0.945，预测效果优于LSTM。

图14。不同神经单网络波动项的位移预测结果。

表2。不同神经网络模型的预测误差。

总体而言，上述三种类型的神经网络在波动项位移曲线的单调增减阶段都取得了较好的预测性能。但在波动项位移曲线的拐点处仍会存在明显的误差，无法达到准确预测的目的。

单个神经网络组合预测波动项位移的情况如图15所示。从整体预测误差来看，组合的两个神经网络模型改善了波动项位移曲线拐点处预测不准确的问题，模型的整体预测精度更高。其中，TCN-BiLSTM的预测性能优于TCN-LSTM。具体分析如下。

TCN具有因果扩展卷积结构和出色的特征提取能力。它可以融合原始特征，获得高维抽象特征，增强特征信息的挖掘。LSTM和BiLSTM时间序列网络具有较强的时间预测能力，可以更好地捕捉输入序列中的模式和关系。lstm型网络可以与TCN网络结合进行波动项位移预测。通过TCN提取特征变量并将其输入到时间序列网络中，大大提高了时间序列网络中存储单元的处理效率。因此，组合预测模型在学习时间序列的复杂交互关系方面更加有效。

图15。带波动项的不同组合神经网络的位移预测结果。

从绝对误差分布直方图上看，TCN-BiLSTM的总体误差分布小于TCN-LSTM。通过计算，得到了利用两种组合网络进行滑坡波动项位移预测的预测误差指标。与TCN - lstm相比，TCN与BiLSTM的组合使MAPE平均降低了71.955%，使得TCN - BiLSTM组合网络的预测精度更高。

4.3.3. 总位移预测

如图16所示，将多项式拟合预测的趋势位移与TCN-BiLSTM联合神经网络预测的波动位移叠加，得到滑坡的总预测位移。通过将滑坡总预测位移与实际值进行对比，发现预测的滑坡总累积位移与实际值高度吻合。总预测位移中，MAPE为0.002,RMSE为0.406,R2为0.999，预测效果较好。

图16。滑坡总位移预测结果。

实验结果表明，该模型对滑坡起伏项位移的预测精度高于其他5种模型。对于非线性波动项位移曲线，曲线拐点处数据点的准确预测至关重要。模型的特征提取和学习能力决定了位移预测的准确性。与LSTM相比，TCN和BiLSTM在单个神经网络中的预测误差更小。这是由于TCN模型具有出色的特征提取能力，可以深入挖掘非线性特征。双向LSTM网络结构可以充分利用输入特征信息，获得更丰富的特征表示进行学习。将TCN与BiLSTM相结合可以实现对非线性特征的准确预测。万家湾滑坡波动项的位移与降雨和地下水位高度有关，这些特征变化在雨季往往是非线性的。因此，构建TCN-BiLSTM组合模型可以更准确地把握滑坡的运动趋势。

另一方面，TCN-BiLSTM组合模型具有较高的复杂度，需要更多的计算资源和训练时间。因此，在训练过程中选择关键的输入特征就显得尤为重要。

5. 结论

本文重点研究了降雨诱发滑坡的高精度位移预测问题，深入分析了影响因素与滑坡累积位移的关系，并结合BiLSTM和TCN的优点，提出了基于TCN - BiLSTM联合结构神经网络的降雨诱发滑坡位移预测模型。并将该预测模型应用于万家湾滑坡的位移预测，并将其预测结果与LSTM、TCN、BiLSTM和TCN - LSTM模型的预测结果进行了比较。得到以下结论:

(1) ICEEMDAN算法对滑坡位移-位移序列分解具有较强的适应性。通过选择合理的信噪比分解，可以将滑坡累积位移有效分解为相对稳定的高频波动项和低频残差项，得到的位移分量具有实际物理意义。

(2)在预测滑坡位移波动项的特征数据选择中，降水、地下水位、滑坡历史位移与滑坡波动项的位移分量高度相关。本文采用GRG-MCI组合筛选方法对处理后的参数数据进行处理，识别出的影响因素与滑坡波动项的位移分量高度相关。

(3)对于滑坡趋势位移预测，采用多项式拟合方法可获得较好的预测结果，预测值R2为0.999，表明预测精度较高，能较准确地反映滑坡位移的趋势变化。在预测滑坡波动项位移时，TCN - BiLSTM组合结构神经网络模型能准确捕捉滑坡位移的波动变化，预测值R2为0.997，优于传统的LSTM、TCN、BiLSTM和TCN - LSTM模型。

(4)本文采用ICEEMDAN-TCN-BiLSTM模型对万家湾滑坡D1监测点位移进行预测。对预测结果的各项评价指标证明，该模型对滑坡位移预测具有较高的适用性。据此推断，该方法可有效应用于其他滑坡位置的位移预测。但其在预测其他类型滑坡位移方面的适用性仍需进一步验证。