当前位置：首页 > news >正文

动态规划背包问题

news 2025/7/4 12:47:34

一、0-1背包问题

0-1背包问题就是给定n个物品和一个容量为C的背包，物品i的重量是Wi,其价值是Vi。问：应该如何选择装入背包的物品，使总价值最大且总重量不超过C？

1.确定状态表示

dp[i][j] 表示在背包容量为j时，从下标为0到i的物品里任意取的最大价值

2.确定边界和遍历顺序

我们最后要求的最大价值就是dp[4][10]的值，第一行和第一列都设置为0当作边界条件

3.找到状态转移方程（核心）

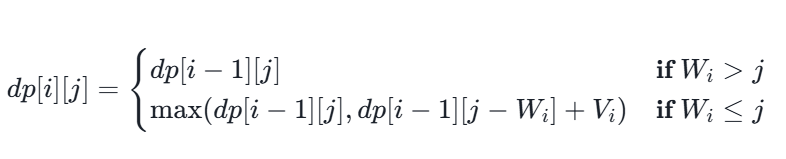
解释：

1.如果物品i的重量Wi大于当前背包容量j，那么无法将物品i放入背包，因此dp[i][j]应该等于考虑前i-个物品时最大价值，既dp[i-1][j].

2.如果物品i的重量Wi小于或等于当前背包重量j，那么我们有两种选择：

（1）不将物品放入背包，此时价值为dp[i-1][j]。

（2）将物品i放入背包，此时价值为dp[i-1][j-Wi]+Vi(既剩余容量为j-Wi的背包中放入前i-1个物品的最大价值加上物品i的价值)。

（3）取两种情况中的最大值作为dp[i][j]

参考代码如下：

class ZeroOneKnapsack {//背包容量W，物品重量数组w，物品价值数组v。返回值为最大价值public static int zeroOneKnapsack(int W, int[] w, int[] v) {//获取物品的数量int N = w.length;//创建一个二维数组dpint[][] dp = new int[N + 1][W + 1];for (int i = 1; i <= N; i++) {for (int j = 0; j <= W; j++) {//判断当前物品的重量是否小于等于当前容量if (w[i - 1] <= j) {//比较物品价值并取最大值dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);} else {dp[i][j] = dp[i - 1][j];}}}//返回考虑所有物品且背包容量为W时的最大价值return dp[N][W];}public static void main(String[] args) {int W = 10; // 背包容量int[] w = {2, 3, 4, 5}; // 物品重量int[] v = {3, 4, 5, 6}; // 物品价值System.out.println("最大价值为：" + zeroOneKnapsack(W, w, v));}
}

二、完全背包问题

完全背包问题与0-1背包问题类似，但存在一个关键区别：完全背包问题中，每种物品的数量是无限的，即每种物品可以选择多次放入背包，而0-1只能选择一次。

1.状态转移方程（核心）

解释：

1.w[i]>j:如果当前物品重量大于背包容量，则无法放入物品，因此dp[i][j]等于考虑前i-1种物品时的最大价值，即dp[i-1][j].

2.w[i]<[j]:如果当前物品重量小于或等于背包容量，则有两种选择：

（1）不放入当前物品，价值为dp[i-1][j]。

（2）放入当前物品，价值为dp[i][j-w[i]]+v[i]

（3）取两者情况最大值作为dp[i][j]的值

参考代码如下：

public class CompleteKnapsack {public static int completeKnapsack(int W, int[] w, int[] v) {int N = w.length;int[] dp = new int[W + 1];for (int i = 0; i < N; i++) {for (int j = w[i]; j <= W; j++) {//状态转移，比较不放入当前物品的价值和放入当前物品的价值，取两者中的最大值。这里dp[j - w[i]] + v[i]表示在容量为j - w[i]的背包中已经达到的最大价值加上当前物品的价值。dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);}}return dp[W];}public static void main(String[] args) {int W = 10;int[] w = {2, 3, 5};int[] v = {2, 4, 7};System.out.println("最大价值为：" + completeKnapsack(W, w, v));}
}

三、多重背包问题

与完全背包问题比，物品选择次数有限。

1.状态转移方程（核心）

参考代码如下：

public class MultipleKnapsack {public static int multipleKnapsack(int W, int[] w, int[] v, int[] n) {//获取物品种类数int N = w.length;//创建一个一维数组dp，其中dp[j]表示背包容量为j时能够达到的最大价值int[] dp = new int[W + 1];for (int i = 0; i < N; i++) {//获取当前物品的数量限制int amount = n[i];//使用二进制思想优化，将物品数量拆分成若干个2的幂次方之和，这样可以减少状态转移的次数。for (int k = 1; amount > 0; k <<= 1) {//计算当前批次可以处理的物品数量，不超过剩余数量amount且不超过kint num = Math.min(k, amount);//amount -= num;：更新剩余数量amount -= num;int weight = w[i] * num;int value = v[i] * num;//从后向前遍历背包容量，这样可以保证每个物品只被计算一次for (int j = W; j >= weight; j--) {dp[j] = Math.max(dp[j], dp[j - weight] + value);}}}//返回背包容量为W时的最大价值return dp[W];}public static void main(String[] args) {int W = 10;int[] w = {2, 3, 5};int[] v = {2, 4, 7};int[] n = {3, 2, 2};System.out.println("最大价值为：" + multipleKnapsack(W, w, v, n));}
}