方差分析（通俗易理解）

方差分析的核心

什么是方差分析

方差分析(Analysis of Variance,ANOVA)是假设检验的一种延续与扩展，主要用来对多个总体均值（三组或三组以上均值）是否相等作出假设检验，研究分类型自变量对数值型因变量的影响。

它的零假设和备择假设分别为：

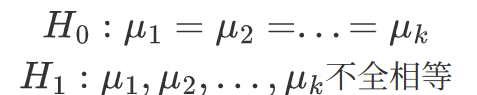
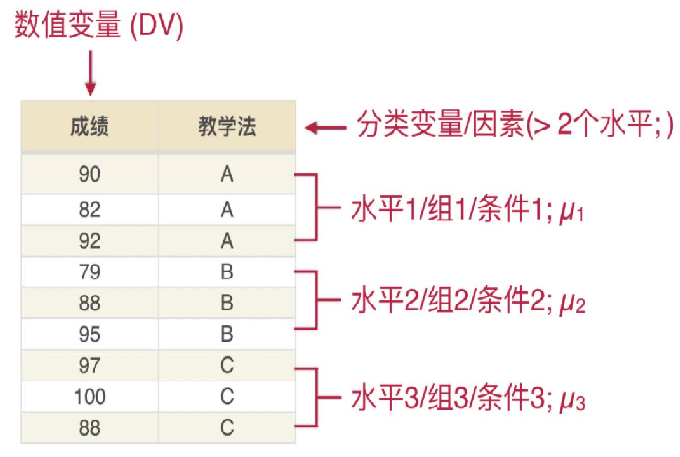
方差分析的核心

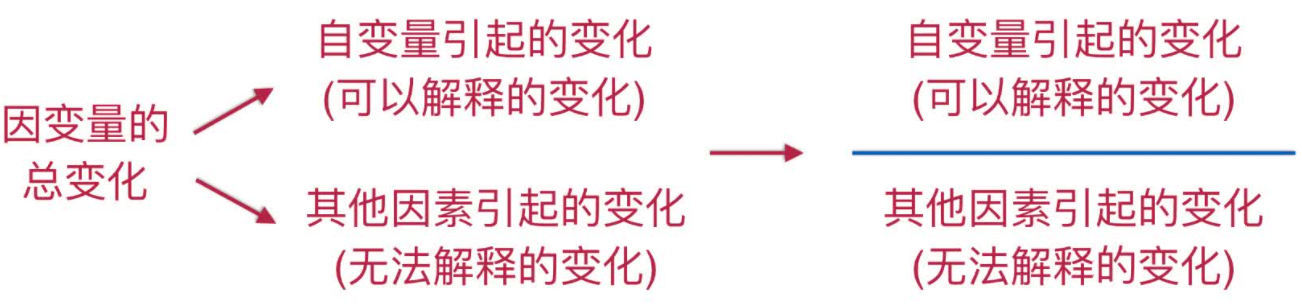
因变量的总变化由两部分引起：

• 自变量引起的变化（可以解释的变化）
• 其他因素引起的变化（无法解释的变化）

自变量引起的变化（可以解释的变化）其他因素引起的变化（无法解释的变化）自变量引起的变化（可以解释的变化）其他因素引起的变化（无法解释的变化）∼F

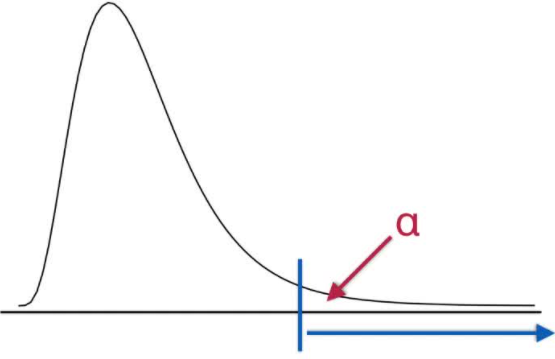
计算得到的F值与临界值进行比较，从而作出拒绝或接受原假设H~0~的判断

单因素方差分析的前提条件

单因素方差分析的前提条件

• 独立性

  • 组内独立（随机抽样、随机分配；样本容量<10%总体容量）
  • 组间独立（非配对）

• 正态性：各组总体服从正态分布

  • 样本容量较大（每组样本容量≥10）时，如果一定程度上违反了正态性，仍可以使用ANOVA
  • 样本容量较小时，如果违反了正态性，则应使用非参数方法进行分析

• 方差齐性：各组总体的方差相等

  • 各组样本的样本容量相等时，如果一定程度上违反了方差齐性，仍可以使用ANOVA
  • 各组样本的样本容量不相等时，如果最大的样本标准差与最小的样本标准差之比不超过2，仍可以使用ANOVA

单因素方差分析

第一步：提出假设

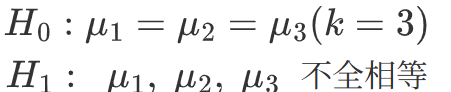
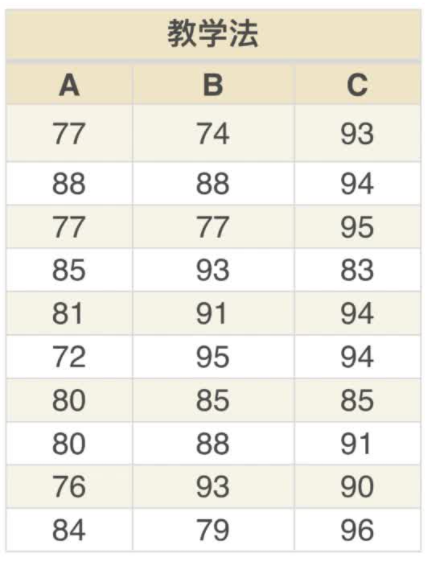
第二步：分别计算各组的平均成绩与总平均成绩

第三步：成绩的总变化（总偏差平方和/总变差)

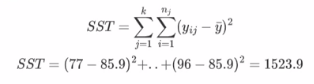
第四步：自变量引起的变化（组间变化/效应平方和）

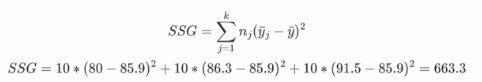
第五步：其他因素引起的变化（组内变化/误差平方和）

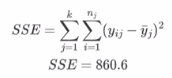
第六步：计算MSG、MSE

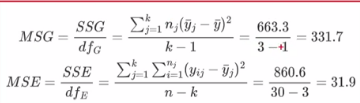
第七步：计算比值

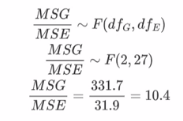
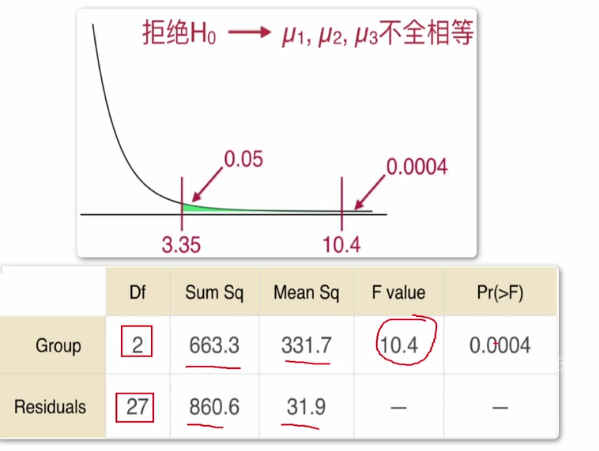
第八步：作出判断

多重比较

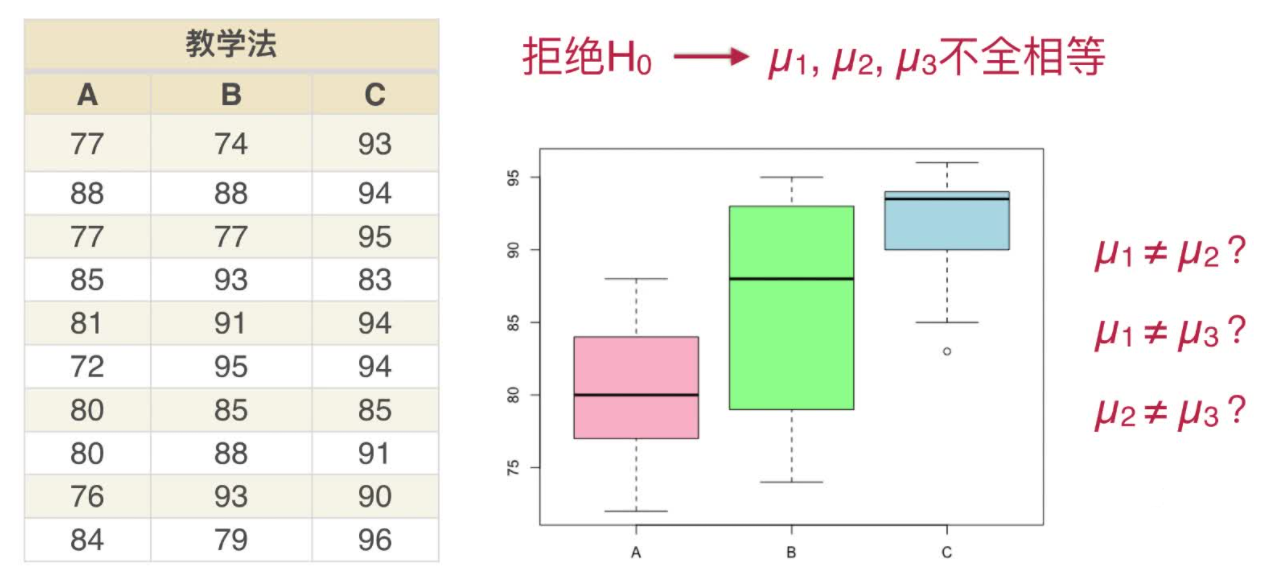
对于方差分析的结论，如果拒绝了原假设H~0~，则有必要进一步分析，到底是哪两组均值不相等，这就是多重比较。

post-hoc(事后检验)

• 方差未知且相等的情况下，对两个总体均值差的检验

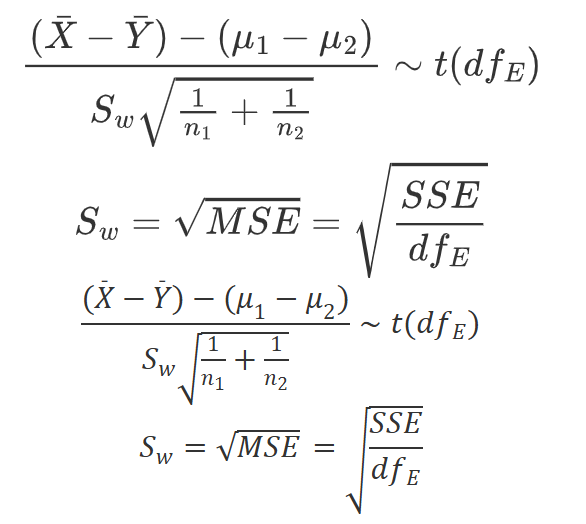
• 校正α

α*=α/比较次数

以比较μ~1~和μ~2~为例：

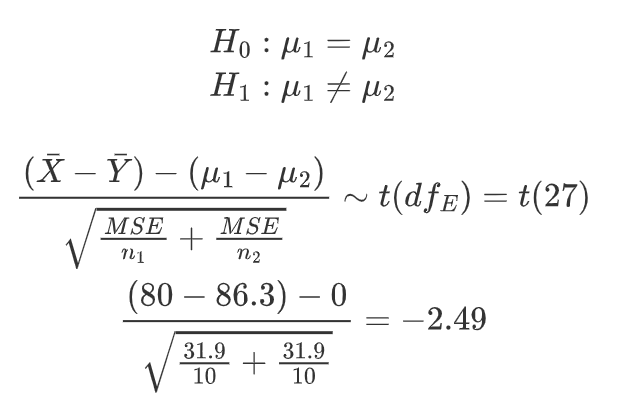
p = 2 * 0.0096=0.019 > α*=0.05/3=0.017 接受H~0~

单因素方差分析的SciPy实现

CCSS案例中提供了2030年4月，以及2030、2031、2032年12月四个时间点的消费者信心监测数据， 现希望分析这四个时间点的消费者信心指数平均水平是否存在差异。这里只使用北京消费者的数据进行分析

import scipy.stats as ss
# 描述北京消费者不同时间的消费信心指数
ccss.query("s0 == '北京'").groupby('time').index1.describe()
a = ccss.query("s0 == '北京' & time == 203004").index1
b = ccss.query("s0 == '北京' & time == 203012").index1
c = ccss.query("s0 == '北京' & time == 203112").index1
d = ccss.query("s0 == '北京' & time == 203212").index1
ss.levene(a, b, c, d) # 方差齐性检验

事后检验

import scikit_posthocs as sp
pc = sp.posthoc_conover(ccss, val_col='index1', group_col='time', p_adjust = 'bonferroni')
# 使用热力图显示比较结果
heatmap_args = {'linewidths': 0.25, 'linecolor': '0.5', 'clip_on': False, 'square': True, 'cbar_ax_bbox': [0.80, 0.35, 0.04, 0.3]}
sp.sign_plot(pc, **heatmap_args)