前两天有小伙伴说想要把常见算法的原理 + 公式汇集起来。
这样非常非常方便查看!分为上下两篇,下篇地址:
本次文章分别从下面6个方面,涉及到20个算法知识点:
-
监督学习算法
-
无监督学习算法
-
半监督学习算法
-
强化学习算法
-
集成学习算法
-
深度学习算法
监督学习算法
监督学习算法是一种通过学习输入数据和相应的标签之间的关系来进行预测或分类的方法。
在监督学习中,模型接收带有标签的训练数据,然后通过学习这些数据的模式来进行预测或分类新的未标记数据。
1、线性回归
线性回归是一种用于建立和分析变量之间线性关系的监督学习算法。它主要用于解决回归问题,即预测一个或多个连续数值型输出(因变量)与一个或多个输入特征(自变量)之间的关系。
基本原理
线性回归基于一个简单的假设,即因变量(输出)与自变量(输入)之间存在线性关系。这意味着我们假设输出可以通过输入的线性组合来预测,其中每个输入特征都与一个权重相乘,然后将它们相加,再加上一个截距(常数项)。
核心公式
考虑一个简单的线性回归问题,其中有一个自变量(特征)x和一个因变量(输出)y。线性回归的基本公式可以表示为: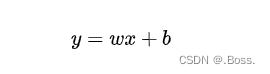
2、逻辑回归
逻辑回归是一种用于解决二分类问题的监督学习算法,其基本原理是使用逻辑函数(也称为Sigmoid函数)来建模因变量(输出)与自变量(输入)之间的概率关系。逻辑回归的目标是估计某个事件发生的概率,通常表示为0或1,例如肿瘤是恶性(1)或良性(0)。
基本原理
逻辑回归基于以下思想:我们希望将线性组合的输出映射到一个介于0和1之间的概率值,以表示事件发生的可能性。为此,逻辑回归使用逻辑函数(Sigmoid函数)来执行这种映射。
核心公式
逻辑回归的核心公式可以表示为: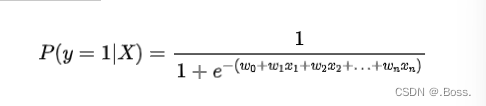
3、决策树
决策树是一种常用的监督学习算法,用于解决分类和回归问题。它的基本原理是根据数据的特征来构建一颗树状结构,树的每个节点代表一个特征,每个分支代表一个特征的取值,叶节点代表输出类别或数值。决策树的目标是通过分裂特征,将数据集划分为纯度更高的子集,以最小化误差或不纯度。
基本原理
决策树的基本原理是根据一系列的规则来做出决策。这些规则是通过对输入特征进行分裂来确定的,每次分裂都会将数据集划分为更加纯净的子集。决策树的构建过程通常分为以下几个步骤:
1、选择一个用于分裂的特征,通常是根据某种度量标准(如信息增益、基尼不纯度等)来选择的,以确保分裂后子集的纯度更高。
2、根据选定的特征和分裂点将数据集划分为子集。
3、递归地应用步骤1和步骤2,直到满足停止条件(如树的深度达到预定值、子集的大小小于某个阈值等)。
4、在叶节点上分配一个输出标签(分类问题)或数值(回归问题),通常是该叶节点中样本的多数类别或均值。
涉及公式
决策树并不涉及像线性回归或逻辑回归那样的具体数学公式,而是通过树的结构来进行决策。然而,有一些用于分裂特征的评估标准,其中最常见的是基尼不纯度和信息增益。这些标准用于选择最佳的分裂点,从而构建更好的决策树。
1、基尼不纯度(Gini Impurity):用于分类问题,表示从数据集中随机选择一个样本,该样本被误分类的概率。基尼不纯度越低,表示数据集的纯度越高。它的数学公式为:
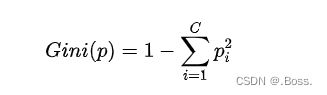
2、信息增益(Information Gain):也用于分类问题,表示在某个特征上进行分裂后,熵(entropy)减少的程度,即数据集的不确定性减少的程度。信息增益越高,表示特征分裂后数据更加纯净。
它的数学公式为: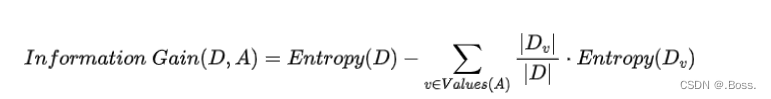
决策树的训练过程旨在最大化信息增益或最小化基尼不纯度,以选择最佳的分裂点。一旦构建好了决策树,就可以使用它来进行分类或回归预测。决策树易于理解和可视化,但在某些情况下可能容易过拟合数据,因此通常需要通过剪枝等技术来提高泛化性能。
4、支持向量机
支持向量机(Support Vector Machine,SVM)是一种强大的监督学习算法,主要用于分类问题,但也可用于回归和异常检测。SVM的基本原理是在特征空间中找到一个最优的超平面,以最大化不同类别之间的间隔,从而使分类更加准确。
基本原理
1、间隔最大化:SVM的目标是找到一个超平面,使不同类别的样本点到这个超平面的距离(间隔)最大化。这个间隔被称为“间隔最大化”。
2、支持向量:在SVM中,只有一小部分样本点对超平面的位置具有影响力,它们被称为“支持向量”。这些支持向量是距离超平面最近的样本点,它们决定了超平面的位置。
3、核技巧:SVM还使用了核函数,可以将数据从原始特征空间映射到一个更高维度的特征空间。这使得SVM可以处理非线性可分的数据。
核心公式
在SVM中,核心公式涉及到以下关键概念:
1、决策函数:用于将输入特征向量映射到超平面并进行分类。决策函数的基本形式如下:
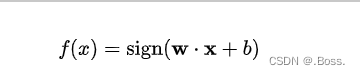
2、间隔:SVM的目标是最大化间隔,其中间隔定义为支持向量到超平面的距离的两倍。支持向量到超平面的距离可以用以下公式表示:
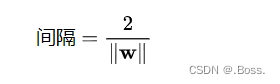
5、K最近邻
K最近邻(K-Nearest Neighbors,简称KNN)是一种常用的监督学习算法,主要用于分类和回归问题。KNN的基本原理是基于特征空间中样本点的距离来进行预测或分类。
对于分类问题,KNN找到与待分类样本在特征空间中最近的K个训练样本,并基于它们的类别标签进行投票决策。对于回归问题,KNN找到最近的K个训练样本,并计算它们的平均值或加权平均值来预测待预测样本的数值输出。
基本原理
1、距离度量:KNN基于样本点之间的距离来度量它们的相似性。通常使用欧几里德距离、曼哈顿距离、闵可夫斯基距离等来计算距离。
2、K值选择:KNN中的K表示选择最近邻的数量。通过选择不同的K值,可以调整模型的复杂性。较小的K值可能会导致模型对噪声敏感,而较大的K值可能会导致模型过于平滑。
3、投票或平均:对于分类问题,KNN对最近的K个训练样本的类别标签进行投票,然后将得票最多的类别标签分配给待分类样本。对于回归问题,KNN计算最近的K个训练样本的数值输出的平均值或加权平均值,并将结果用作待预测样本的输出。
核心公式
KNN的核心公式涉及到距离度量和K个最近邻的选择。
1、距离度量:KNN使用距离度量来计算样本之间的距离。对于两个样本点 和 ,欧几里德距离的计算公式为:

2、K个最近邻的选择:对于分类问题,KNN选择与待分类样本距离最近的K个训练样本,然后根据它们的类别标签进行投票决策。对于回归问题,KNN选择与待预测样本距离最近的K个训练样本,然后计算它们的数值输出的平均值或加权平均值来预测。
KNN是一种简单而直观的算法,它不需要训练过程,但在处理大规模数据集时可能会变得计算密集。选择合适的距离度量和K值是KNN的关键,通常需要根据具体问题进行调整和优化。
此外,KNN在处理不平衡数据和高维数据时可能会表现不佳,因此需要谨慎选择适用场景。
无监督学习算法
无监督学习算法是从未标记的数据中自动发现隐藏的模式和结构,而无需事先提供标签或目标。
1、K均值聚类
K 均值聚类(K-Means Clustering)是一种常见的无监督学习算法,用于将数据集划分为K个不同的簇(cluster),使得每个数据点属于距离其最近的簇的中心点。
K均值聚类的基本原理是通过迭代优化,将数据点分配给簇并更新簇的中心点,以最小化每个数据点到其所属簇中心点的距离平方和(称为“簇内平方和”或“Inertia”)。
基本原理
1、随机初始化:首先,随机选择K个数据点作为初始簇中心点。
2、分配数据点:对于每个数据点,计算其与各个簇中心点的距离,并将其分配到距离最近的簇中心点所属的簇。
3、更新簇中心点:对于每个簇,计算该簇内所有数据点的平均值,将其作为新的簇中心点。
4、重复迭代:重复步骤2和步骤3,直到簇中心点不再发生明显变化,或者达到预定的迭代次数。
K均值聚类的目标是最小化以下损失函数(簇内平方和):
K均值聚类的结果是将数据点划分为K个簇,并且每个簇由一个中心点表示。这个算法通常需要多次运行,并在不同的初始簇中心点选择下进行迭代,以找到全局最优解。K均值聚类是一种简单而有效的聚类算法,但它对初始簇中心点的选择敏感,并且需要指定K的值。
2、主成分分析
主成分分析(Principal Component Analysis,PCA)是一种常用的降维技术和数据分析方法,用于减少数据集的维度,同时保留数据中的主要信息。PCA的基本原理是通过线性变换将高维数据投影到一个低维的子空间,以找到最大方差的方向,这些方向被称为主成分。
基本原理
1、数据中心化:首先,对原始数据进行中心化处理,即将每个特征的均值减去每个数据点的对应特征值,以确保数据的均值为零。
2、协方差矩阵:然后,计算数据的协方差矩阵,该矩阵表示了不同特征之间的关联性。
3、特征值分解:对协方差矩阵进行特征值分解,找到其特征值和特征向量。
4、选择主成分:选择具有最大特征值的特征向量,这些特征向量构成了数据在低维子空间上的新坐标轴,被称为主成分。
5、投影:将原始数据投影到所选的主成分上,从而实现数据的降维。
核心公式
1、数据中心化:对于一个包含m个样本和n个特征的数据矩阵X,首先计算每个特征的均值,然后进行中心化处理,得到中心化的数据矩阵X:
3、高斯混合模型
高斯混合模型(Gaussian Mixture Model,GMM)是一种概率模型,用于对多个高斯分布组合来建模数据分布。它在许多领域中都有广泛的应用,包括聚类、密度估计、异常检测等。GMM的基本原理是假设数据是由多个高斯分布组合而成,每个高斯分布被称为一个组件。以下是GMM的基本原理和核心公式:
基本原理
1、高斯分布的线性组合:GMM假设数据是由K个高斯分布组合而成的,其中K是用户定义的分量数量。每个高斯分布被称为一个组件,表示数据在不同区域的概率密度。
2、隐变量:每个数据点都与一个隐变量相关联,这个隐变量表示数据点属于哪个组件。通常,这个隐变量是一个离散的变量,取值范围为1到K。
3、生成数据的过程:生成一个数据点的过程如下:
-
首先,选择一个组件(隐变量的取值),确定数据点属于哪个高斯分布。
-
然后,根据选定的组件的高斯分布生成具体的数据点。
4、参数估计:通过最大似然估计等方法,估计每个组件的均值、方差和混合系数,以拟合数据。
核心公式
1、高斯分布的概率密度函数:高斯分布的概率密度函数是GMM的核心组成部分,表示了数据在每个组件上的分布。对于一维高斯分布,概率密度函数为:
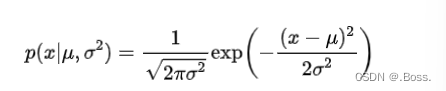
2、GMM的概率密度函数:GMM的概率密度函数是多个高斯分布的线性组合,表示了数据在整个模型上的分布。对于一维数据,GMM的概率密度函数为:
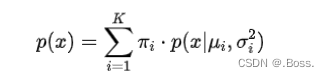
4、层次聚类
层次聚类(Hierarchical Clustering)是一种基于数据相似性的聚类算法,它的基本原理是通过不断地合并或分割数据点,创建一个层次化的聚类结构。
层次聚类可分为两种主要类型:凝聚型(Agglomerative)和分裂型(Divisive)。凝聚型聚类从每个数据点作为一个单独的簇开始,然后逐渐合并相似的簇,直到所有数据点都属于一个大簇。分裂型聚类则从所有数据点属于一个大簇开始,然后逐渐分割簇,直到每个数据点都成为一个单独的簇。
基本原理
1、初始状态:将每个数据点视为一个单独的簇,形成初始的N个簇,其中N是数据点的数量。
2、相似性度量:计算每对簇之间的相似性,通常使用距离度量(如欧几里德距离、曼哈顿距离、相关性等)来度量簇内数据点之间的差异。
3、合并最相似的簇:选择最相似的两个簇,将它们合并成一个新的簇。合并的规则通常包括单链接(single linkage)、完全链接(complete linkage)、平均链接(average linkage)等。
4、重复合并:重复步骤3,继续合并最相似的簇,直到只剩下一个簇,或者满足预定的停止条件(如簇的数量等)。
涉及公式
层次聚类没有明确的核心数学公式,因为它的操作涉及到相似性度量和合并规则的选择,这些规则会影响聚类的结果。
1、相似性度量:通常使用距离度量来计算两个簇之间的相似性。例如,两个簇A和B之间的距离可以使用欧几里德距离表示:
其中,和是两个簇内的数据点的特征值。
2、合并规则:选择合并两个簇的规则会影响聚类的结果。例如,单链接合并规则下,两个簇之间的距离通常是两个簇内距离最近的数据点之间的距离。完全链接合并规则下,两个簇之间的距离通常是两个簇内距离最远的数据点之间的距离。
3、树状图(Dendrogram):层次聚类的结果通常表示为一棵树状图,树的每个节点代表一个簇或合并的簇,叶子节点代表单个数据点。树状图可以用于选择合适的聚类数量。
层次聚类的优点包括不需要事先指定聚类数量,结果可以以层次化的方式展示数据之间的相似性,但它的计算复杂度相对较高。选择合适的相似性度量和合并规则以及聚类数量是层次聚类中的关键问题。
5、自编码器(Autoencoders)
自编码器(Autoencoder)是一种神经网络架构,用于无监督学习和特征学习。它的基本原理是通过学习数据的紧凑表示(编码),然后再从该编码中重建原始数据,从而可以用来提取数据的关键特征、降低数据维度、去噪以及生成新数据。自编码器通常由两部分组成:编码器(Encoder)和解码器(Decoder)。
基本原理
1、编码器(Encoder):编码器将输入数据映射到低维度的编码空间,通常通过一系列神经网络层来实现。编码器的目标是将输入数据压缩到一个紧凑的表示,捕获数据的关键特征。
2、解码器(Decoder):解码器将编码后的表示映射回原始数据空间,也通常通过一系列神经网络层来实现。解码器的目标是从编码中重建尽可能接近原始数据的输出。
3、重建损失(Reconstruction Loss):自编码器的训练过程包括最小化输入数据与解码器输出之间的重建损失,通常使用均方差(Mean Squared Error,MSE)作为损失函数。重建损失衡量了重建数据与原始数据之间的差异,促使自编码器学习捕捉数据的重要特征。
4、降维和特征学习:自编码器可以用来实现数据降维,通过减小编码的维度,从而提取数据的关键特征。编码器的隐藏层表示可以被视为数据的压缩表示。
核心公式
自编码器的核心公式涉及到编码和解码过程,以及重建损失的计算。
1、编码过程:编码器将输入数据 映射到编码表示 ,可以表示为: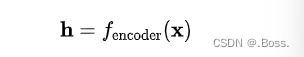
未完待续。。








![[数据集][目标检测]蕃茄核桃桔子龙眼青枣5种水果检测数据集VOC+YOLO格式270张5类别](https://img-blog.csdnimg.cn/direct/79dd1c8a5a7747e29c0c2b50b7fa354d.png)