软考中级习题与解答——第一章_数据结构与算法基础(2)
例题11

1、知识点总结
顺序查找
基本思想:从数组一端(通常是第一个元素)开始,逐个比较元素,直到找到目标元素或遍历完所有元素。

折半查找
基本思想:仅适用于有序数组,每次将查找范围缩小一半(取中间元素与目标比较,确定目标在左半段或右半段)。

2、最终答案:B
例题12

1、知识点总结
哈夫曼编码的核心性质:哈夫曼编码是一种前缀编码,即任何一个字符的编码都不是另一个字符编码的前缀(这样解码时才不会混淆)。
2、选项分析
选项 A:编码为 111、110、10、01、00。
- 检查前缀关系:
111不是110的前缀,110不是10的前缀,其他编码间也不存在 “一个编码是另一个编码的前缀” 的情况。 - 结论:符合哈夫曼编码的前缀性质。
选项 B:编码为 000、001、010、011、1。
- 检查前缀关系:
1是000、001、010、011的前缀吗?不是(0开头的编码与1开头的编码无包含关系);其他编码间也不存在前缀关系。 - 结论:符合哈夫曼编码的前缀性质。
选项 C:编码为 001、000、10、01、11。
- 检查前缀关系:所有编码间,没有任何一个编码是另一个编码的前缀。
- 结论:符合哈夫曼编码的前缀性质。
选项 D:编码为 110、100、101、11、1。
- 检查前缀关系:
1是11的前缀(11以1开头),同时1也是110、100、101的前缀(这些编码都以1开头)。 - 结论:存在 “一个编码是另一个编码的前缀” 的情况,不符合哈夫曼编码的前缀性质。
3、最终答案:D
例题13

1、知识点总结
空指针域
在普通的二叉链表(每个节点存 data、left、right 指针)中,很多节点的 left 或 right 指针是空的(NULL),这些空的指针位置就叫 “空指针域”。
比如下面这棵二叉树的二叉链表表示:
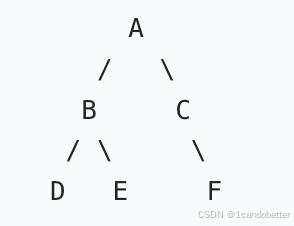
- 节点
D的left和right都是空(没有子节点); - 节点
E的right是空; - 节点
F的left和right都是空; - 这些空的
left/right指针,就是空指针域。
线索化的核心:利用空指针存 “前驱 / 后继”
线索化的目的是:把这些空指针域利用起来,存储节点在 “遍历序列” 中的前驱或后继节点,这样就能快速找到 “谁是当前节点的下一个 / 上一个节点”,不用再递归 / 循环遍历。
遍历序列有三种:先序(根 - 左 - 右)、中序(左 - 根 - 右)、后序(左 - 右 - 根)。
2、选项分析
选项 A:先序线索二叉树找 “先序后继”
先序遍历顺序:根 → 左子树 → 右子树(比如例子中先序是 A → B → D → E → C → F)。
- 先序线索化后,每个节点的空指针会存 “先序下的后继”。
- 规律:如果节点有左子节点,左子节点就是先序后继;如果没有左子节点,右子节点就是先序后继。
- 所以能高效找到,线索化有用。
选项 B:中序线索二叉树找 “中序后继”
中序遍历顺序:左子树 → 根 → 右子树(例子中中序是 D → B → E → A → C → F)。
- 中序线索化后,利用空指针存 “中序后继”。
- 规律很清晰:比如 “左子树最右节点的后继是根,根的后继是右子树最左节点”,线索化后能直接通过指针找到,非常高效。
- 这也是线索化最经典、最有效的场景。
选项 C:中序线索二叉树找 “中序前驱”
和 “找中序后继” 对称,中序线索化也会存 “中序前驱”。
- 规律:比如 “右子树最左节点的前驱是根,根的前驱是左子树最右节点”,同样能通过线索快速找到。
选项 D:后序线索二叉树找 “后序后继”
后序遍历顺序:左子树 → 右子树 → 根(例子中后序是 D → E → B → F → C → A)。
- 后序的 “后继” 依赖关系特别复杂:
- 比如节点
B的后序后继是F,但B和F之间没有直接的父子 / 兄弟关系,依赖整个树的结构; - 再比如最后一个节点
A(根),它的后继不存在,但找前面节点的后继时,需要知道 “父节点的右子树是否遍历完”。
- 比如节点
- 后序线索化后,空指针存的信息不足以覆盖所有后继的复杂依赖,所以很难高效找到后序后继。
3、最终答案:D
例题14

1、知识点总结
平衡二叉树
平衡二叉树是一种二叉搜索树,其每个节点的左右子树的高度差(平衡因子)的绝对值不超过 1。平衡因子的计算方式为:平衡因子 = 左子树高度 - 右子树高度。当插入或删除节点导致平衡因子的绝对值大于 1 时,树会失去平衡,需要通过旋转操作(左旋、右旋、左右旋、右左旋)来恢复平衡。
二叉搜索树
二叉搜索树是一种二叉树,它满足左子树的所有节点值 < 根节点值 < 右子树的所有节点值,并且左、右子树也都是二叉搜索树(递归满足该性质)。简单来说,就是 “左小右大”,通过这个性质可以快速进行查找、插入、删除等操作
二叉搜索树与 “遍历顺序” 的关系
二叉搜索树是树的一种 “数据组织形式”(定义了节点值的分布规则),而 “先序、中序、后序” 是二叉树的 “遍历方式”(访问节点的顺序规则),二者属于不同概念:
- 先序遍历:顺序是「根 → 左子树 → 右子树」。
- 中序遍历:顺序是「左子树 → 根 → 右子树」。
- 后序遍历:顺序是「左子树 → 右子树 → 根」。
对于二叉搜索树来说,中序遍历的结果是 “升序排列” 的(因为左子树 <根 < 右子树,中序遍历会按 “左 - 根 - 右” 依次访问,自然得到升序序列),这是二叉搜索树的一个重要特性,常用来验证一棵树是否为二叉搜索树。
2、选项分析
在构造平衡二叉树(以及普通二叉搜索树)时,根节点的选择通常是由 “插入顺序” 决定的
图中是按 “27 → 16 → 75 → 38 → 51” 的顺序插入节点,每一步都遵循二叉搜索树的插入规则:
插入 27:
这是第一个节点,直接作为根节点(此时树中只有 27)。插入 16:
16 小于 根节点 27,所以插入到 27 的左子树,成为 27 的左孩子。插入 75:
75 大于 根节点 27,所以插入到 27 的右子树,成为 27 的右孩子。插入 38:
38 需要和根节点 27 比较:38 > 27 → 进入右子树;
再和右子树的根节点 75 比较:38 < 75 → 插入到 75 的左子树,成为 75 的左孩子。插入 51:
51 需要和根节点 27 比较:51 > 27 → 进入右子树;
再和右子树的根节点 75 比较:51 < 75 → 进入 75 的左子树;
再和左子树的根节点 38 比较:51 > 38 → 插入到 38 的右子树,成为 38 的右孩子。
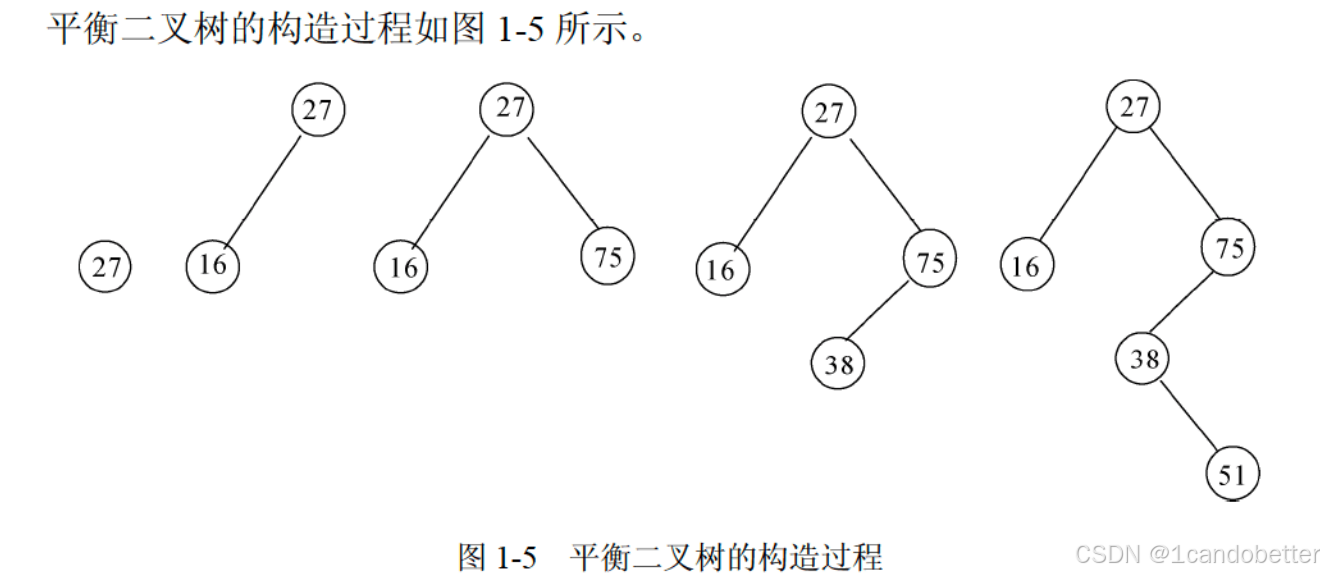
3、最终答案:D
例题15

1、知识点总结

无向完全图属于连通图。因为无向完全图中任意两个顶点之间都有一条直接的边,所以任意两个顶点之间必然存在路径(直接走这条边即可),满足 “连通图中任意两个顶点之间都存在路径” 的定义,因此无向完全图是连通图。
2、选项分析

3、最终答案:B
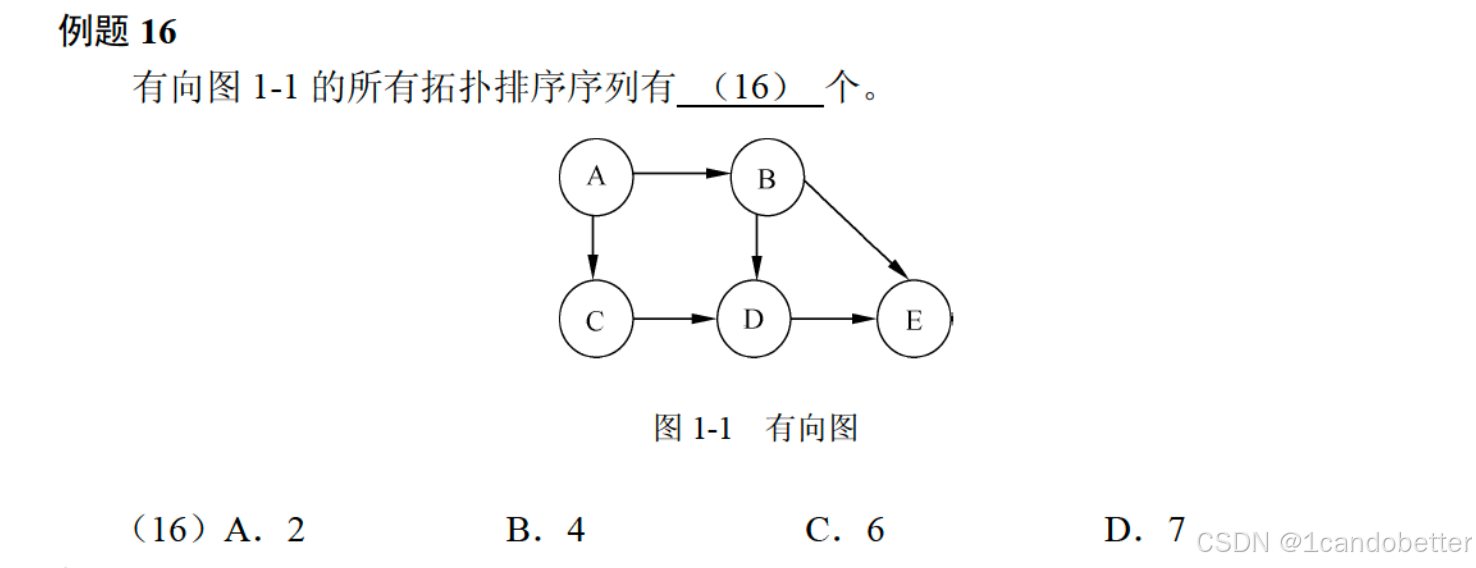
例题16
1、知识点总结
有向无环图
“有向” 指边有方向;“无环” 指图中不存在 “从一个顶点出发,沿着边能回到自身” 的循环。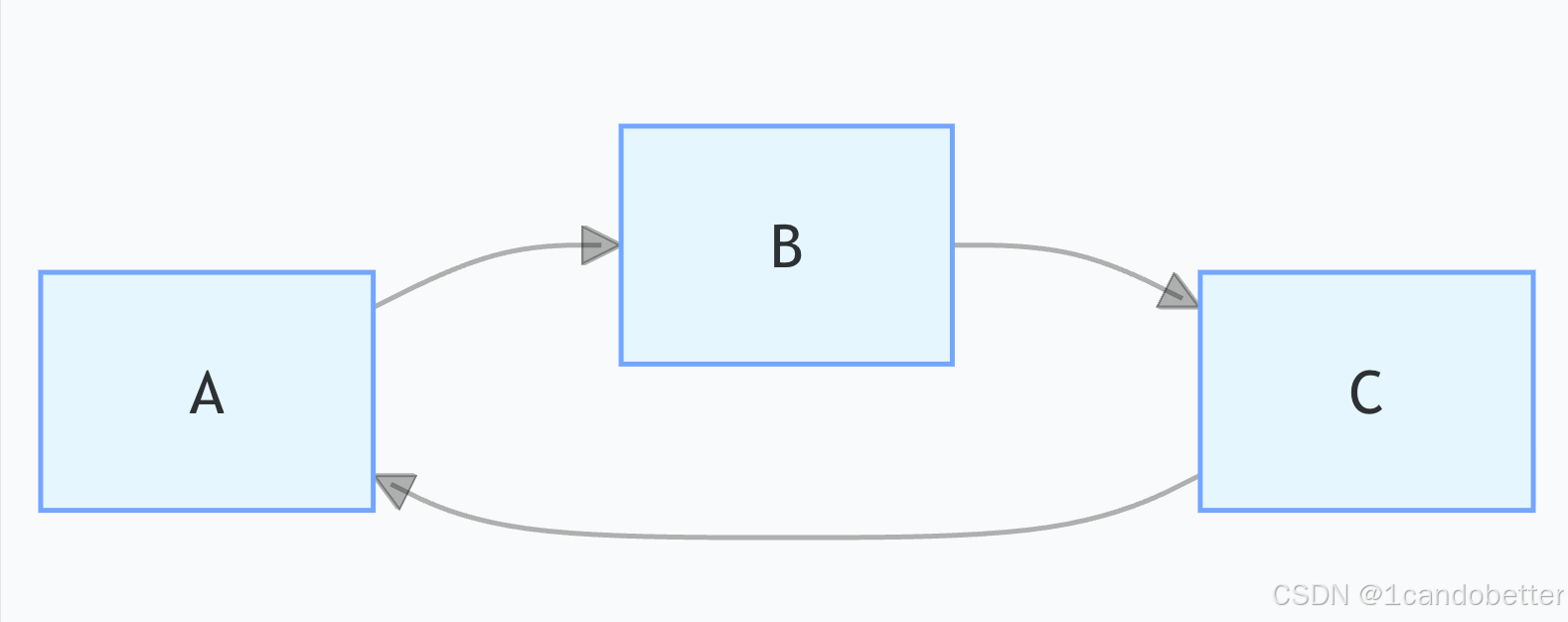
而题目中的图是有向无环图(DAG),因为所有边的方向不会形成循环。
拓扑排序
拓扑排序是对 DAG 的顶点进行排序,使得:对于每一条有向边 u->v,顶点 u 在排序结果中都出现在 v 之前。
2、选项分析
拓扑排序的核心步骤是:每次选 “入度为 0” 的顶点(没有任何边指向它的顶点),输出后删除它的所有出边,重复直到所有顶点输出。

A**DE剩下需排列的是 B 和 C,它们的位置需满足:
- 位于 A 之后、D 之前;
- B 和 C 之间无严格依赖(因为 B 和 C 都是 A 的直接后继,且互相之间没有边)。
根据 B 和 C 的排列,只有 2 种合法序列:
- (A, B, C, D, E)
- (A, C, B, D, E)
3、最终答案:A
例题17

1、知识点总结
本题涉及下三角矩阵的压缩存储,核心是利用下三角矩阵 “上三角元素全为 0,仅需存储下三角非零元素” 的特点,通过行优先顺序将二维矩阵的非零元素映射到一维数组中,需要推导非零元素 (A[i,j]) 在一维数组中的存储位置公式。
2、选项分析

3、最终答案:A
例题18

1、知识点总结
冒泡排序的核心思想是重复地走访要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。一趟冒泡排序会从序列的起始位置开始,依次比较相邻的两个元素,将较大的元素 “冒泡” 到序列的末尾(升序排序时)。
2、选项分析
原序列为:Q, H, C, Y, P, A, M, S, R, D, F, X(共 12 个元素),进行升序冒泡排序的一趟扫描(从前往后比较相邻元素,大的往后换),过程如下:

3、最终答案:D
例题19

1、知识点总结

2、选项分析
插入排序比较次数计算(数组:<3, 1, 4, 1, 5, 9, 6, 5>,共 8 个元素):
插入排序的核心思想是:从第二个元素开始,将每个元素视为“待插入”的牌,在它左边已经排好序的“手中牌”里,从右到左逐个比较,找到合适的位置插入

归并排序比较次数计算(数组:<3, 1, 4, 1, 5, 9, 6, 5>,共 8 个元素):
归并排序采用“分治”策略,先将数组不断拆分,再将有序的子数组两两合并。比较只发生在合并阶段。
第一轮合并 (合并长度为1的子数组)
- merge(<3>, <1>) -> <1, 3> (比较1次)
- merge(<4>, <1>) -> <1, 4> (比较1次)
- merge(<5>, <9>) -> <5, 9> (比较1次)
- merge(<6>, <5>) -> <5, 6> (比较1次)
本轮比较次数:4
第二轮合并 (合并长度为2的子数组)
merge(<1, 3>, <1, 4>)
1 vs 1 (1次)
3 vs 1 (1次)
3 vs 4 (1次)
-> <1, 1, 3, 4> (共3次比较)
merge(<5, 9>, <5, 6>)
5 vs 5 (1次)
9 vs 5 (1次)
9 vs 6 (1次)
-> <5, 5, 6, 9> (共3次比较)
本轮比较次数: 3 + 3 = 6
第三轮合并 (合并长度为4的子数组)
merge(<1, 1, 3, 4>, <5, 5, 6, 9>)
1 vs 5 (1次)
1 vs 5 (1次)
3 vs 5 (1次)
4 vs 5 (1次)
左侧子数组已全部合并,右侧剩余元素直接放入,不再需要比较。
-> <1, 1, 3, 4, 5, 5, 6, 9> (共4次比较)
本轮比较次数: 4
归并排序总共需要 4 + 6 + 4 = 14 次比较。
3、最终答案:A
例题20

1、知识点总结
递归算法的执行过程主要分为两个阶段:
- 递推阶段:从原问题出发,不断将问题分解为规模更小的子问题,直到达到递归的终止条件(基本情况)。
- 回归阶段:从递归的终止条件开始,逐步向上返回,将子问题的解合并成原问题的解。
