Part 1️⃣：相机几何与单视图几何-第六章：相机模型

Part 1️⃣介绍

这一部分主要探讨单视角相机的几何学，包含三个章节。

第六章描述了3D场景空间到2D图像平面的投影过程。相机映射由一个矩阵表示，对于点的映射而言，这是一个3×4矩阵P，它将3D空间中世界点的齐次坐标映射到图像平面上成像点的齐次坐标。该矩阵通常具有11个自由度，相机属性（如相机中心和焦距）可从中提取。特别地，内部相机参数（如焦距和纵横比）被封装在一个3×3矩阵K中，该矩阵可通过简单分解从P获得。相机矩阵有两类特别重要的类型：有限相机和中心位于无穷远处的相机（如表示平行投影的仿射相机）。

第七章阐述了在给定一组对应世界点和图像点坐标的情况下，如何估计相机矩阵P。本章还讨论了如何有效将相机约束融入估计过程，以及校正径向透镜畸变的方法。

第八章涵盖三个主题：首先讨论相机对除有限点外的其他几何对象的作用，包括直线、圆锥曲线、二次曲面和无穷远点。无穷远点/直线的图像是消失点/线。第二个主题是相机标定，即在不计算整个矩阵P的情况下，计算相机矩阵的内部参数K，重点阐述内部参数与绝对圆锥图像的关系，以及如何通过消失点和消失线标定相机。最后介绍标定圆锥——这是一种用于可视化相机标定的简单几何工具。

6.1有限远相机

6.1.1 基础针孔相机模型

根据上述，实际上这个投影过程就是一个从3D欧式空间到2D欧式空间的一个映射。所以，这里是基于相机成像的相似三角形原理，刚好巧妙的把深度Z作为了齐次坐标的最后一维w。最后，这个z=f为相机的焦距。

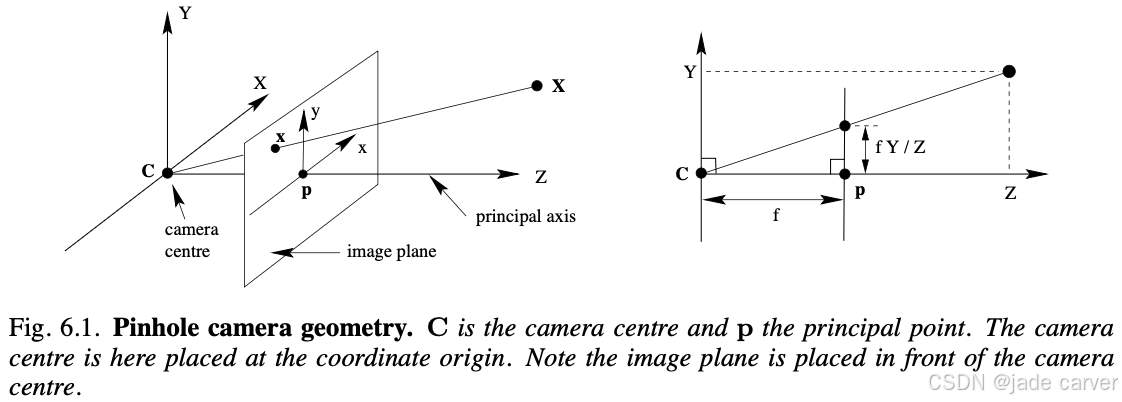
6.1.2 主点偏移与校准矩阵 K

上面的模型是规则形态，即主点p位于图像原点（0，0），现在考虑一般情况，即主点位于其他位置：

相机坐标系：

一般情况介绍完了，回头再考虑相机位置如果还是在原点呢，此时我们将该坐标系称为相机坐标系：

矩阵K被称为相机标定矩阵（也叫校准矩阵）。在公式中，我们将(X, Y, Z,1)T表示为Xcam是为了强调：我们假设相机位于欧几里得坐标系的原点，且相机的主轴与Z轴重合，而Xcam点正是在该坐标系下表示的。这样的坐标系可称为相机坐标系框架。

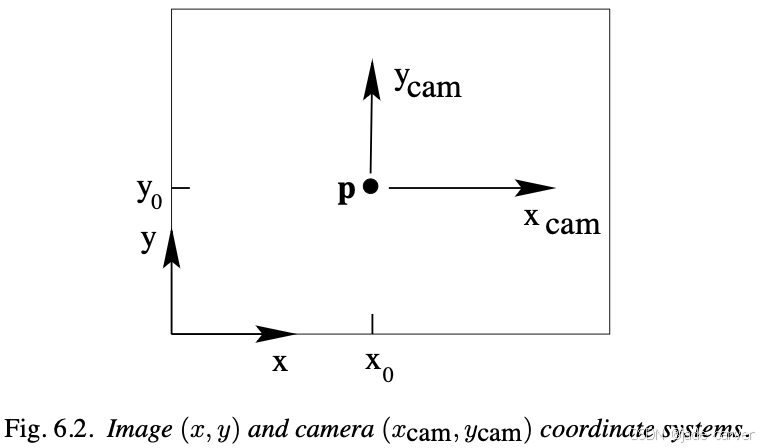
6.1.3世界坐标系与外参

通常情况下，空间中的点会以另一个欧几里得坐标系（称为世界坐标系）表示。这两个坐标系之间通过旋转和平移相关联（见图6.3）。

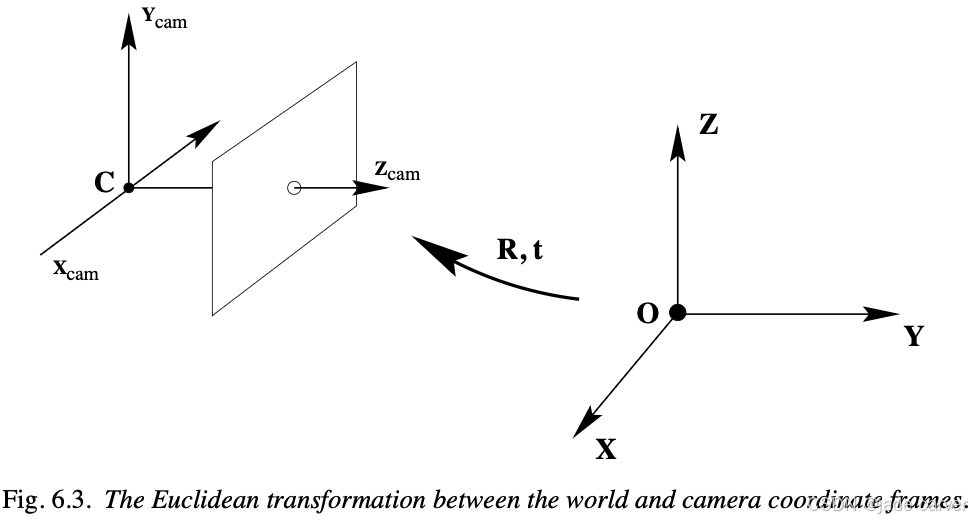
若 是一个非齐次3维向量，表示某点在世界坐标系中的坐标，而表示该点在相机坐标系中的坐标，则它们之间的关系可表示为：

其中， 表示相机中心在世界坐标系中的坐标，R 是一个 3×3 的旋转矩阵，表示相机坐标系的朝向。该方程可写成齐次坐标形式：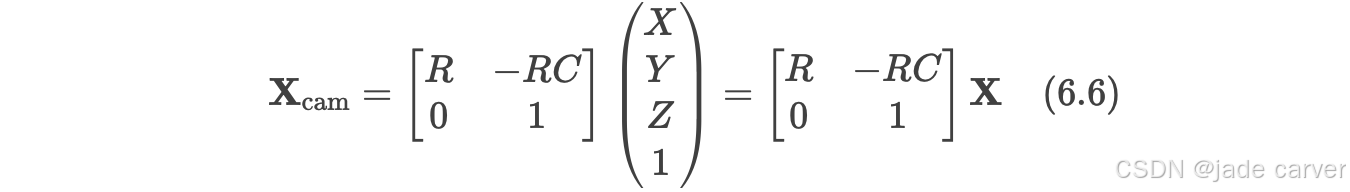

将其与 (6.5) 式结合，可得：

其中，X 现在位于世界坐标系中。这就是针孔相机的一般映射关系。可以看出，一个通用的针孔相机 具有 9 个自由度：

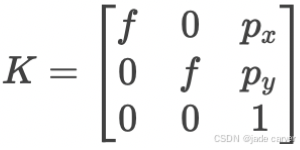• 包含 3 个参数（）
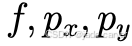• R 包含 3 个参数
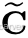•  包含 3 个参数

为什么R只有3个自由度：

K 中的参数称为相机内参（internal camera parameters）或内部定向（internal orientation），而 R 和 C 的参数用于描述相机朝向和位置与世界坐标系的关系，称为外参（external parameters）或外部定向（exterior orientation）。

有时，不显式表示相机中心会更方便，而是将世界坐标系到图像的变换表示为