简单聊聊光栅化技术

参考文章

https://zhuanlan.zhihu.com/p/450540827

https://zhuanlan.zhihu.com/p/27846162

光栅化技术做了什么？

关于光栅化，广义上来说，就是将连续的几何图元转换为离散的像素片段。这听起来是不是还是有点的抽象，接下来，我来逐步解释这些概念。

光栅化技术的应用：

光栅化技术的一个主要应用场景就是：将现实中的3D物体，转化到二维的显示屏上。

光栅化技术原理解释：

这里首先有一个问题，就是现实世界中的真实物体，如何在计算机中表示？显然，现实中的物体是连续的，可以认为是由无数多点构成的。显然计算机并不能通过模拟这无数个点的坐标来还原现实中的物体。

一种常见的处理方式是：用许多小的三角块来模拟现实中的真实物体。为什么这么做呢？因为三个点构成一个平面，这样，采用微元的思想，只要有足够多的三角块，就能够还原出现实中的某个物体。

事实上，物体的3D建模也可以采用这种方式。当然，三角形是最简单的，现在也有了更复杂的其他多边形。

这种方法有点像计算机绘制直线一样，本质上是许多点；在计算机中绘制3D物体的表面，本质上也可以是许多的小三角形。

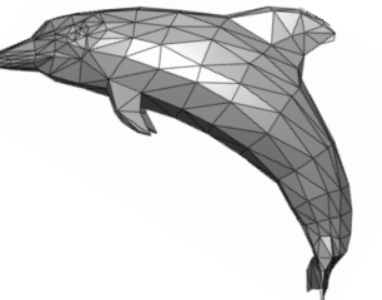
回到定义，这里连续的几何图元就可以指代3D场景中的三角形或其他多边形等。

对于上面提到的三角形，因为是在3D空间中，用于形成物体的表皮轮廓，姑且称为3D三角形，以区别于接下来提到的2D三角形；

对于一个3D三角形，我们显然可以用三组三维坐标来衡量。比如某个3D三角形的三个顶点A（x，y，z）B（x，y，z）C（x，y，z）。

现在又有了新的问题，我们知道屏幕是由像素构成的，一个屏幕可以看做是许多个离散的像素点构成的。而且屏幕是一个二维空间，那么如何将某个3D物体，在2D的屏幕上显示呢？

这就需要构建一种映射关系，也即实现前文提及的将每个3D三角形映射到屏幕上的2D三角形。

这里的2D三角形，最明显的特征就是少了z这个维度，也可以用三个点来表示A’（x，y）B’（x，y）C’（x，y）

而屏幕上的某个2D三角形，又是由许多的像素点构成的。所以，再次回看光栅化的作用：将连续的几何图元，转换为离散的像素片段。是不是好理解了一点。

光栅化的任务就是解决了一个关键问题：3D空间中的几何图元，用屏幕中的哪些像素来表示，以及怎么表示？

关于3D高斯泼溅技术：

3D高斯泼溅技术是一种3D重建技术，他的创新点在于，使用了大量的高斯粒子来重建物体。这一点是和常用的方法如三角形来重建，是有显著的不同。

这里的高斯粒子也可以称为“高斯椭球”，每个高斯椭球包含了位置，协方差矩阵，颜色等参数信息。通过光栅化技术，可以得到对应某个相机角度下的图片，这样就可以通过反向传播的方式来不断修正每一个高斯粒子，以优化3D高斯重建的效果。

关于“高斯椭球”，严格意义上，他并不是一个像三角形这样的椭球面之类的“几何面”，而是一个概率密度分布，而协方差矩阵正是控制这个概率分布的形状的参数。