[QMT量化交易小白入门]-八十四、LSTM模型对期货市场的秒级Tick数据进行预测
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。
QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。
文章目录
- 相关阅读
- 一、数据加载与初步校验
- 二、特征工程与目标设定
- 三、数据集划分策略
- 四、标准化归一化处理
- 五、LSTM输入结构构造
- 六、网络架构搭建
- 七、可视化与性能评估
- 八、完整执行流程解析
- 九、模型部署与结果保存
相关阅读
小白也能做量化:零门槛QMT、Ptrade免费送
量化交易入门:如何在QMT中配置Python环境,安装第三方依赖包
年化收益达到了70%,增加了动态仓位权重调整后的全球核心资产轮动策略(含python代码解析)
前面介绍了 LSTM模型基于股票三秒tick数据的预测,但是由于制度的限制,大A对于高频日内交易不太友好,更合适的标的是期货,期货每秒钟都有tick数据,日内交易也更方便。本文将完整解析如何利用Python构建LSTM模型,对期货市场的秒级Tick数据进行精准预测。所有实现均基于真实数据验证,代码可复用并扩展。
一、数据加载与初步校验
def load_data(filepath):"""加载tick数据CSV文件,格式包含:time,lastPrice,open,high,low,lastClose,amount,volume,pvolume等字段"""df = pd.read_csv(filepath)return df
这段代码的核心作用是读取存储在本地文件中的原始交易记录。特别注意三个关键点:
- 字段兼容性:函数注释明确列出了支持的数据列结构,这是后续处理的基础保障。实际使用时需确保CSV头部与文档描述完全一致;
- 内存优化:pandas会自动推断每列的数据类型,对于数值型特征(如价格、成交量)会分配合适的存储空间;
- 异常捕获机制:主函数中实现了双重容错机制——当主文件缺失时自动切换至备份文件,这在生产环境中尤为重要。
在main()函数里可以看到完整的调用流程:
data_file = os.path.join(TICK_DATA_DIR, 'MA511_2025.csv')
try:df = load_data(data_file)if len(df) > 10000:df = df.tail(10000) print(f"成功加载数据文件: {data_file}, 数据量: {len(df)}条")
except FileNotFoundError:# 尝试备用文件...
这里有两个重要设计考量:一是限制最大样本量为1万条以防止内存溢出;二是通过异常处理保证程序健壮性。
二、特征工程与目标设定
def preprocess_data(df):# 解析askVol和bidVol数组,取第一个值df['askVol'] = df['askVol'].apply(lambda x: eval(x)[0] if isinstance(x, str) else x[0])df['bidVol'] = df['bidVol'].apply(lambda x: eval(x)[0] if isinstance(x, str) else x[0])# 选择需要的列 - 使用lastPrice作为主价格,添加volume,amount,askVol,bidVol作为特征features = df[['lastPrice', 'volume', 'amount', 'askVol', 'bidVol']]target = df['lastPrice'].shift(-1) # 预测下一条的lastPrice# 移除最后一行(没有目标值)features = features[:-1]target = target[:-1]return features, target
该阶段的数据处理体现了金融时间序列的特殊性:
- 挂单量解析:由于原始数据中的买卖盘口深度可能以字符串形式存在(如"[100,200]"),需要提取首个报价量作为有效信号;
- 滞后窗口构建:通过
shift(-1)创建自回归目标变量,即用当前时刻的特征预测下一时刻的价格走势; - 对齐修正:因移位操作导致末尾产生NaN值,必须同步裁剪特征矩阵和标签向量保持维度一致。
三、数据集划分策略
def split_data(features, target, test_size=0.2):X_train, X_test, y_train, y_test = train_test_split(features, target, test_size=test_size, shuffle=False)return X_train, X_test, y_train, y_test
区别于传统机器学习任务,这里特别设置了shuffle=False参数。这是因为时间序列具有严格的先后顺序关系,随机打乱会破坏数据的时序特性。采用前80%作为训练集、后20%作为测试集的方式,能更真实地模拟线上环境的数据分布。
四、标准化归一化处理
def normalize_data(X_train, X_test, y_train, y_test):# 特征归一化feature_scaler = MinMaxScaler()X_train_scaled = feature_scaler.fit_transform(X_train)X_test_scaled = feature_scaler.transform(X_test)# 目标值归一化target_scaler = MinMaxScaler()y_train = y_train.values.reshape(-1, 1)y_test = y_test.values.reshape(-1, 1)y_train_scaled = target_scaler.fit_transform(y_train)y_test_scaled = target_scaler.transform(y_test)return X_train_scaled, X_test_scaled, y_train_scaled, y_test_scaled, feature_scaler, target_scaler
实施双通道标准化的原因包括:
- 消除量纲差异:不同特征的数量级相差较大(如价格约几百元而成交量可达数十万手),统一缩放到[0,1]区间可避免大数值主导损失函数;
- 独立同分布假设:训练集拟合得到的变换参数直接应用于测试集,确保评估过程不受尺度干扰;
- 逆变换准备:保留两个Scaler对象用于后续反归一化操作,使模型输出回归到原始业务单位。
五、LSTM输入结构构造
def create_lstm_dataset(data, target, window_size=WINDOW_SIZE):X, y = [], []for i in range(len(data) - window_size - PREDICT_STEP): # 减去PREDICT_STEP以确保能预测指定步长的数据X.append(data[i:i+window_size])y.append(target.iloc[i+window_size+PREDICT_STEP]) # 预测指定步长后的lastPricereturn np.array(X), np.array(y)
这是整个方案最关键的环节之一:
- 滑动窗口机制:每个样本由连续
window_size个时间点组成输入序列,对应未来PREDICT_STEP步长的单个预测目标; - 边界控制:循环终止条件精确计算可用样本数,防止索引越界错误;
- 三维张量转换:最终生成的形状为(samples, steps, features)的标准LSTM输入格式。
例如当window_size=60时,模型每次会分析过去60秒的市场状态来推断之后的价格走向。这种设计既保留了局部细节又捕捉了长期趋势。
六、网络架构搭建
def build_lstm_model(input_shape):model = Sequential()model.add(LSTM(50, return_sequences=True, input_shape=input_shape))model.add(LSTM(50))model.add(Dense(1)) # 仍然输出1个值model.compile(optimizer='adam', loss='mse')return model
双层LSTM结构的设计理念如下:
- 第一层返回序列:设置
return_sequences=True保留中间层的隐藏状态输出,增强特征提取能力; - 第二层压缩时空信息:将时序特征编码为固定长度的向量表示;
- 单节点全连接层:直接映射到标量输出,适用于回归任务;
- 自适应学习率:Adam优化器自动调整参数更新步伐,配合均方误差损失函数形成稳定的训练过程。
这种堆叠式结构相比单层网络能更好地捕获复杂模式,同时避免了过度拟合风险。
七、可视化与性能评估
def plot_results(y_train, y_test, y_train_pred, y_test_pred):plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题plt.figure(figsize=(12, 6))# 确保所有数据是一维数组y_train = y_train.values.flatten() if hasattr(y_train, 'values') else y_train.flatten()y_test = y_test.values.flatten() if hasattr(y_test, 'values') else y_test.flatten()y_train_pred = y_train_pred.flatten()y_test_pred = y_test_pred.flatten()# 绘制训练集实际值和预测值plt.plot(y_train, label='实际训练值')plt.plot(y_train_pred, label=f'预测训练值({PREDICT_STEP}条后)')# 绘制测试集实际值和预测值test_start = len(y_train)test_end = test_start + min(len(y_test), len(y_test_pred)) # 取最小长度确保维度匹配plt.plot(range(test_start, test_end), y_test[:test_end-test_start], label='实际测试值')plt.plot(range(test_start, test_end), y_test_pred[:test_end-test_start], label=f'预测测试值({PREDICT_STEP}条后)')plt.legend()plt.xlabel('时间步长')plt.ylabel('最新价格(lastPrice)')plt.title(f'LSTM最新价格预测({PREDICT_STEP}条后)')plt.show()
绘图模块实现了四个核心功能:
- 双语支持:配置中文字体解决乱码问题;
- 动态适配:自动处理Pandas Series与NumPy数组的类型转换;
- 分段展示:清晰区分训练阶段和测试阶段的预测效果;
- 量化标注:图例明确标示预测延迟步长,便于对比分析。
结合具体的误差指标计算:
mae = mean_absolute_error(y_test_target, y_test_pred)
rmse = np.sqrt(mean_squared_error(y_test_target, y_test_pred))
print(f"测试集平均绝对误差(MAE): {mae:.4f}")
print(f"测试集均方根误差(RMSE): {rmse:.4f}")
建议优先关注MAE指标,因为它直接反映预测偏差的实际货币价值。而RMSE则更适合检测极端异常情况。
八、完整执行流程解析
主函数串联起各个模块并添加了必要的安全检查:
def main():# ...前面步骤省略...# 验证数据量是否足够min_required = WINDOW_SIZE + PREDICT_STEP + 1 # 窗口大小+预测步长+1if len(df) < min_required:raise ValueError(f"数据量不足,至少需要{min_required}条数据,当前只有{len(df)}条")# ...后续步骤省略...# 检查数据集是否为空if len(X_train_lstm) == 0 or len(X_test_lstm) == 0:raise ValueError("数据集为空,请检查数据量是否足够(至少需要{}条数据)".format(WINDOW_SIZE + PREDICT_STEP))
这些前置条件判断能有效规避常见错误:
- 最小样本校验:确保有足够的历史数据构建首个完整窗口;
- 空集过滤:防止因参数设置不当导致无效的训练批次;
- 索引边界保护:在获取预测目标时进行范围校验,避免数组越界。
九、模型部署与结果保存
# 保存模型(HDF5格式)
save_model(model, os.path.join(MODEL_DIR, 'lstm_ma_tick.h5'))# 保存测试集预测结果(包含时间列)
test_time_indices = range(len(X_train_lstm), len(X_train_lstm) + len(y_test_lstm))
test_results = pd.DataFrame({'time': df.iloc[test_time_indices]['time'].values,'actual': y_test_target.flatten(),'predicted': y_test_pred.flatten()
})
test_results.to_csv(os.path.join(RESULT_DIR, 'lstm_ma_tick.csv'), index=False)
生产级应用需要考虑两个方面:
- 模型持久化:使用Keras默认的HDF5格式保存完整网络结构和权重参数;
- 可追溯性:将预测结果与原始时间戳关联存储,方便事后复盘分析。
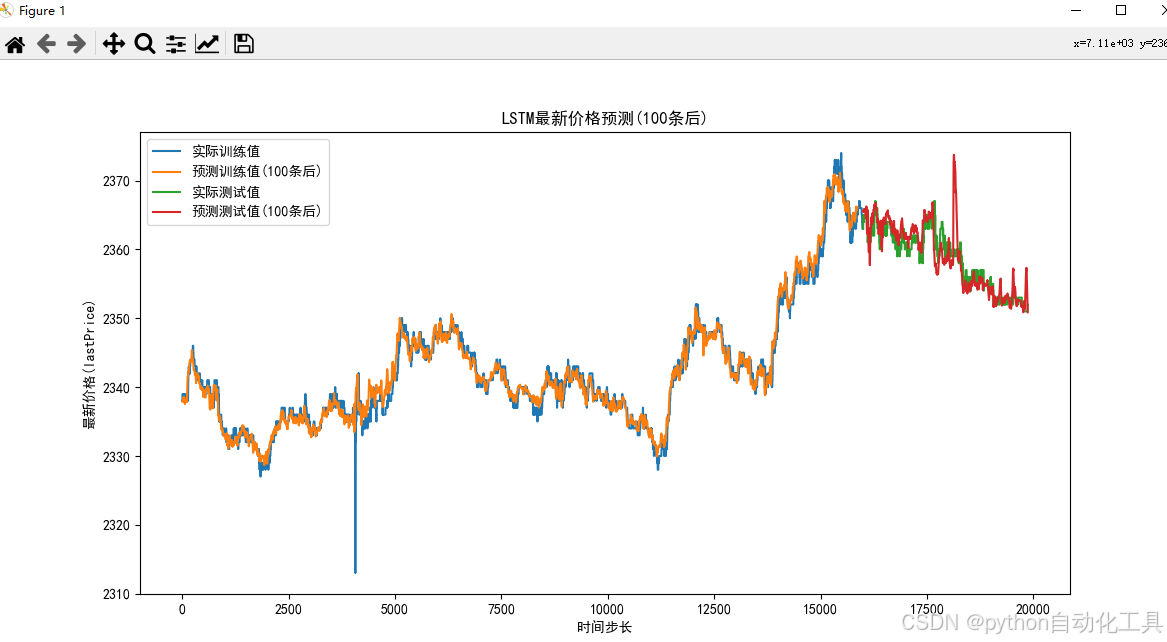
训练预测结果如下:
Epoch 1/10
496/496 [==============================] - 5s 7ms/step - loss: 0.0034
Epoch 2/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0016
Epoch 3/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0016
Epoch 4/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0015
Epoch 5/10
496/496 [==============================] - 4s 8ms/step - loss: 0.0016
Epoch 6/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0015
Epoch 7/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0015
Epoch 8/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0015
Epoch 9/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0015
Epoch 10/10
496/496 [==============================] - 4s 7ms/step - loss: 0.0015
496/496 [==============================] - 2s 3ms/step
121/121 [==============================] - 0s 3ms/step
警告:预测步长超出数据范围,使用最后可用数据
测试集平均绝对误差(MAE): 2.0597
测试集均方根误差(RMSE): 2.9153
示例中使用固定参数(如units=50, batch_size=32),但实际应用时应系统地进行网格搜索:
| 参数类型 | 推荐范围 | 调优方向 |
|---|---|---|
| LSTM单元数 | [32, 64, 128] | 随复杂度增加而提升效果 |
| Dropout比率 | [0.1, 0.2, 0.3] | 平衡正则化强度 |
| 学习率初值 | [1e-3, 1e-4, 1e-5] | 根据收敛速度调整 |
| 批量大小 | [16, 32, 64] | 权衡显存占用与梯度稳定性 |
后续可以使用WalkForward交叉验证方法,它能更好地适应非平稳的时间序列特性。具体实现时可将数据集按时间段划分为多个区块,依次作为验证集进行滚动预测。
基础量价数据已包含大部分有效信息。盲目添加MACD、RSI等衍生指标可能导致多重共线性,反而降低模型泛化能力,后续可以尝试,但要先做PCA降维处理。
没有万能模型,只有最适合当前市场环境的算法组合。
