LeakyReLU和ReLU的区别

提示：坚持更新，坚持学习，更多知识还在探索中

一、ReLU (Rectified Linear Unit - 整流线性单元)

ReLU（整体流性单元）

ReLU是深度学习中最基础、最尝使用的激活函数之一。

• 数学公式：f(x)= max(0, x)=最大值(0,x)
  简单来说，如果输入x是正数，输出就是x；如果是负数，输出就是0

• 优点：
  1.计算简单： 只涉及比较和取最大值操作，没有指数、三角函数等复杂运算，速度极快。这是它在深度学习中被广泛采用的关键原因之一。
  2.缓解梯度消失： 在正区间，其导数为 1，能够有效地将梯度原封不动地传递到前层，极大地缓解了深层网络中的梯度消失问题（相对于 Sigmoid 和 Tanh 而言）。
  2.稀疏激活性： 会让一部分神经元的输出为 0，从而使得网络变得稀疏，减少了参数的相互依存关系，缓解过拟合问题。

• 缺点：
  1.Dead ReLU Problem (神经元死亡问题)： 这是 ReLU 最主要的缺陷。如果一个神经元在训练过程中，其权重更新后，对于所有训练数据的输入该神经元的输出都是负数（即落入 ReLU 的左侧完全平坦区域），那么它的梯度将永远为 0。这意味着之后的训练过程中，这个神经元将永远无法被激活，相当于“死亡”了，其权重也不再更新。
  2.非零中心： ReLU 的输出均值恒大于零，这可能会对后续的权重更新造成轻微的影响（需要更仔细地调整学习率等参数）。

二、LeakyReLU (带泄露的整流线性单元)

LeakyReLU 是针对 ReLU 的“Dead ReLU”问题而提出的改进版本。

• 数学公式：f(x) = max(ax, x)
  这里的a是一个很小的常数（例如0.01或0.1）.如果输入的x是正数，输出就是x；如果是负数，输出不再是0，而是a*x（一个很小的负数值）

• 优点：
  1.解决了“Dead ReLU”问题： 这是其核心优势。因为在负区间梯度不再是 0（而是一个很小的值 α），所以即使神经元输出为负，其梯度也不会完全消失，权重仍然有机会得到更新，神经元有机会“复活”。
  2.保留了 ReLU 的优点： 计算同样简单（只是多了一个乘法操作），在正区间梯度仍然是 1，缓解梯度消失的效果一样好。

• 缺点：
  1.效果不一致： LeakyReLU 的效果并不总是稳定的，其性能提升在一定程度上依赖于超参数 α 的选择。虽然通常设为 0.01，但这个值并不总是最优的。
  2.引入新超参： 需要手动尝试或通过交叉验证来调整 α 的值，增加了模型设计的复杂度。
  LeakyReLU 还有一个变体叫做 PReLU (Parametric ReLU)，它将 α 也作为一个可学习的参数，让网络在训练过程中自己学习出最适合的斜率，这通常能取得比固定 α 更好的效果，但计算量会稍大一些。

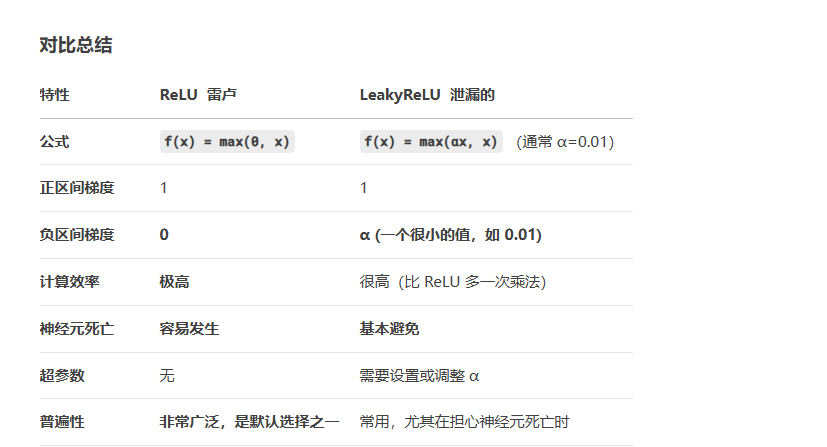
总结

未完待续，，，更多知识还在探索中~