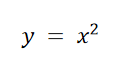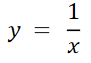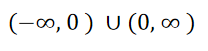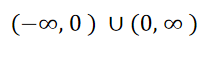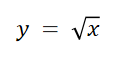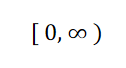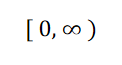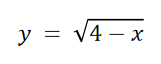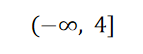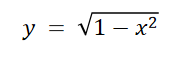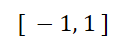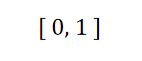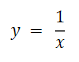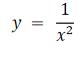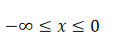我从零开始学微积分(2)- 函数与图形
二、函数与图形
函数是用数学术语来描述现实世界的主要工具。本节讨论函数基本概念,其图形、移位或复合函数的方法。讲述出现在微积分中若干重要的函数类型。
2.1 函数
一个变量的值常取决于另一个变量的值。
如:
- 水达到沸点的温度取决于海拔高度(越往上走,沸点越下降)
- 你的存款额在一年中的增长取决于银行的利率
上述情形中,一个变量的值取决于另一个变量的值。
(1)水的沸点b取决于海拔高度e;
(2)利息的多少I取决于利率r;
我们称b和I为因变量,因为它们是它们所依赖的变量e和r的值所决定的。变量e和r为自变量。
对一个集合中的每个元素制定另一个集合中唯一确定的一个元素的规则称为函数。集合可以是任意类型的集合,而且两个集合不必是相同的。函数类似于对每个允许的输入指定一个唯一确定的输出的机器。输入构成函数的定义域(domain);输出构成了函数的值域(range)(如下图)。

定义:函数
从集合D到集合R的一个函数是对D中每个元素指定R中唯一确定的元素的一种规则。
在这种定义下,D是函数的定义域而R是包含值域的一个集合(如下图)
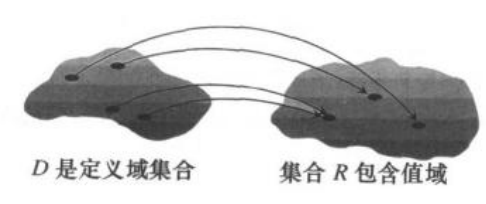
(a)从集合D到集合R的函数;

(b)不是函数,这种指定不是唯一确定的。
许多年前,瑞士数学家欧拉(Leonhard Euler, 1707-1783)首创用符号来说“y 是 x 的函数"的方法:
y = f(x),
念作"y 等于 'f' 'x' "。这种记号使我们能改变所用字母给不同函数以不同名称。如:
说沸点是海拔高度的函数,可以记为b = f(e);
说圆面积是半径的函数,可以记为A = A(r),给函数与因变量同样的名字;
记号y = f(x)还给出记忆函数特定值的方法。f在a处的值可以记作f(a)。
例1(圆周-面积函数)
圆周-面积函数A(r) = 的定义域是所有可能的半径的集合,它是全体正实数构成的集合。值域也是全体正实数构成的集合。
A在r = 2处的值是
即半径为2的圆的面积为
2.2 定义域和值域
例1中,函数定义域是由问题的背景限定的:自变量是半径,因而必须为正。当我们用公式定义函数y = f(x)且没明显说出定义域或由问题的背景所限定,则假定该定义域是使x值处都给出实数y值的最大集合,即自然定义域。如果我们要以某种方式限制定义域,我们必须指明。的定义域是整个实数集。为限制函数,可以说,x为正值,则写作
。
实自变量的许多实值函数的定义域和值域是区间或区间的组合。区间可以是开、闭或半开的,以及有限无限的。
有限区间
(1) 名称:开区间
记号: 或
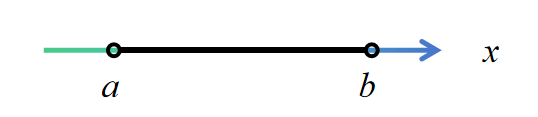
(2) 名称:在a闭在b开
记号: 或
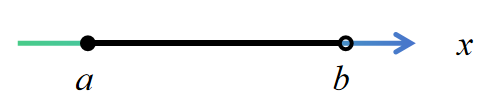
(3) 名称:在a开在b闭
记号: 或

(4) 名称:闭区间
记号: 或
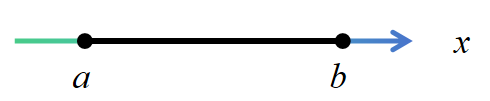
无穷区间
在实数直线上的半直线或实数直线本身。记号∞(无穷)知识为了用起来方便;并非意味着它是一个数。
(5) 名称:全体实数集
记号:![]()
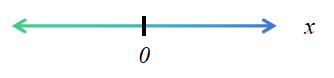
(6) 名称:大于a的数集
记号:![]()
![]()
(7) 名称:大于等于a的数集
记号: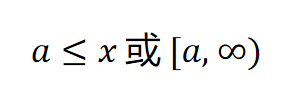

(8) 名称:小于b的数集
记号:![]()
![]()
(9) 名称:小于等于b的数集
记号:![]()
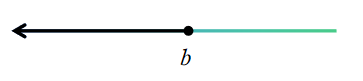
区间的端点称为边界点,它们构成了区间的边界。其余点都是内点,它们构成了区间的内部。包括所有边界点在内的区间都是闭区间。不包含边界点的区间就是开区间。开区间的每一点都是该区间的内点。
例2 (识别定义域和值域) 检验这些函数的定义域。
| 函数 | 定义域(x) | 值域(y) |
|---|---|---|
|  | 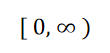 |
|
|
|
|
|
|
|
|
|
|
|
|
解:(1)对任何实数x,方程y = 给出实y值,所以定义域为
![]() 。
。
(2)对除x = 0外的任何实x值,方程![]() 给出实y值。我们不能用0除任何数。
给出实y值。我们不能用0除任何数。
(3)仅当4 - x大于或等于0时,方程![]() 给出实y值。
给出实y值。
(4)对从-1到1的闭区间上的任何x值,方程![]() 给出实y值。在该区间外,1-
给出实y值。在该区间外,1-是负的,从而其平方根不是实数。定义域是
![]()
2.3 审阅和解释图形
平面上的点(x, y),其坐标为函数y = f(x)的输入-输出对,构成函数的图形。例如,函数y = x + 2的图形是坐标(x, y)满足y = x + 2的点的集合。
用笔和纸作图发展图形绘制的技巧,用绘图器作图发展图形审阅技巧。
2.3.1 图形审阅技巧
① 识别图形是合理的
② 看出图形的所有重要特征
③ 解释这些特征
④ 识别绘图器的失效
识别图形是合理的能力来自经验,需要知道基本的函数,它们的图形以及表示它们的方程改变时会怎样影响到其图形的变化。
当绘图器画出的图形不精确时,甚至不正确会发生绘图器失效,通常是由于绘图器分辨率局限造成的。
例3(识别绘图器的失效)求y = f(x) = 的定义域和值域。
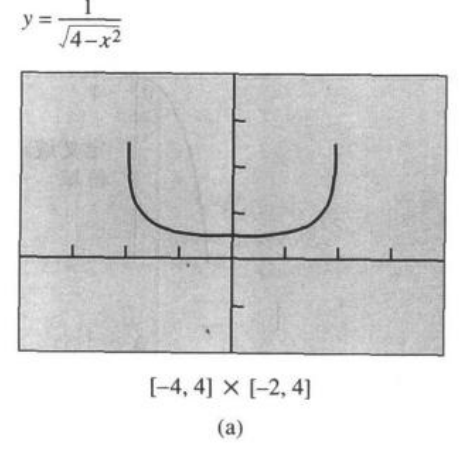
(a) 上述绘图器失效
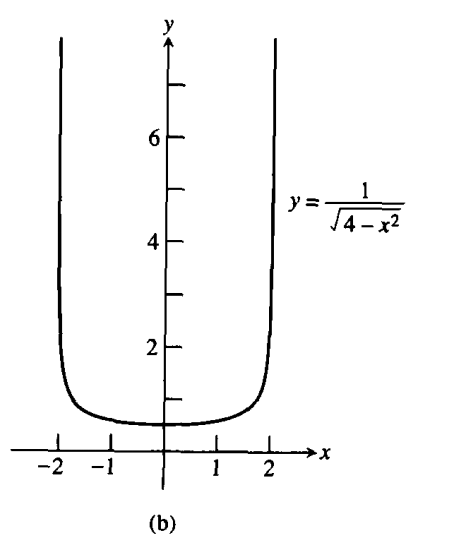
(b)上述的比较精确的图形
解:图(a)中f的图形似乎暗示f的定义域在-2和2之间,而值域也是一个有限区间。后者的观察结果是由绘图器的失效造成的;这时我们可以用代数法来识别这种失效。
代数求解:表达式
因此,,从而定义域为
。
f的最小值为 ,且在x = 0处达到。如下面表所示(f的值舍入到三位小数),当x从左边趋于2或从右边趋于-2时,f的值变得非常大。
| x | ±1.99 | ±1.999 | ±1.9999 | ±1.99999 |
|---|---|---|---|---|
| f(x) | 5.006 | 15.813 | 50.001 | 158.114 |
f的值域为 [0.5, -∞)
下面各图展示了微积分中经常出现的幂函数的图形。知道这些图形的一般形状将会帮助识别绘图器的失效。
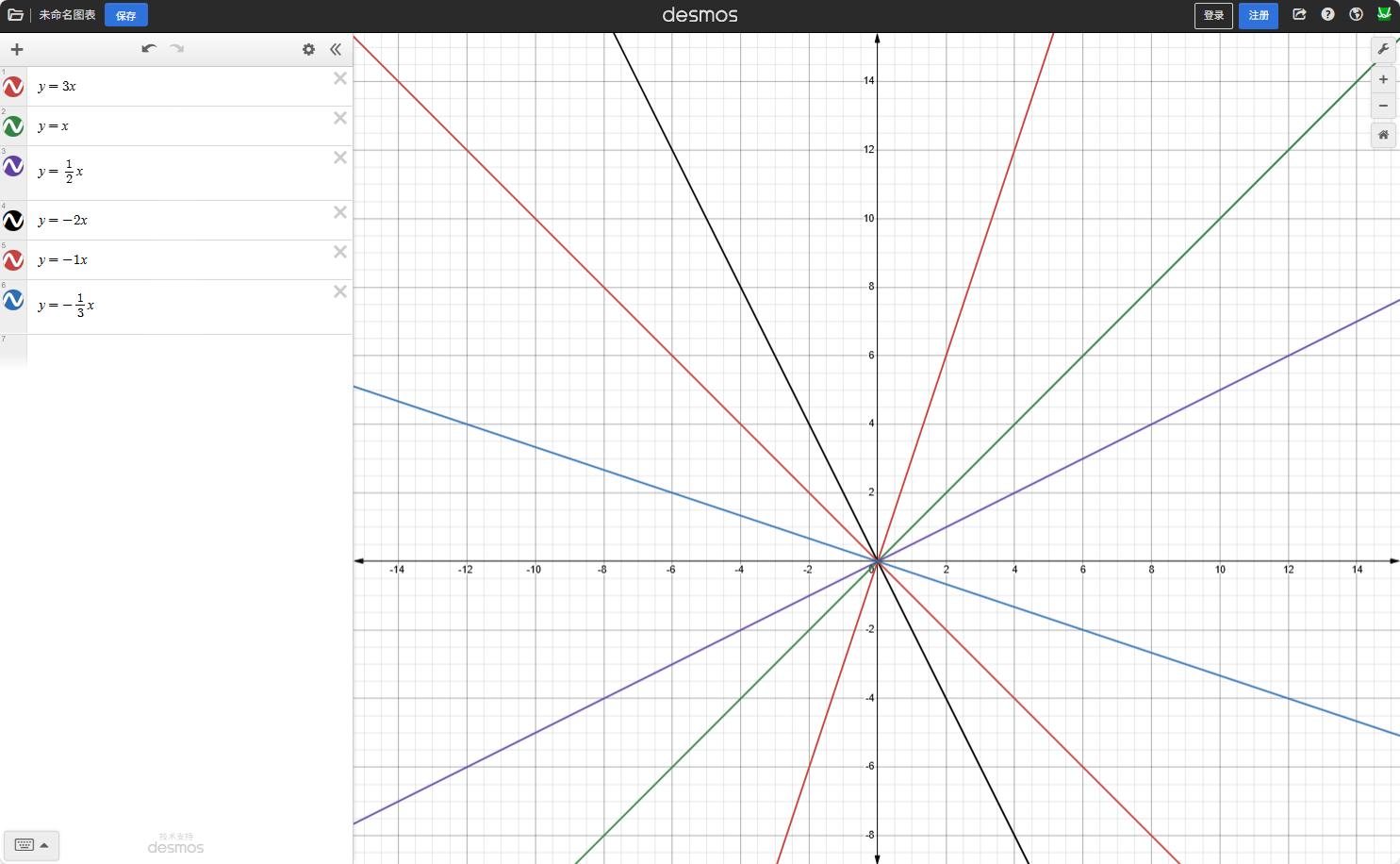
y = mx,对所选的m值
定义域:-∞ < x < ∞
值域:-∞ < y < ∞
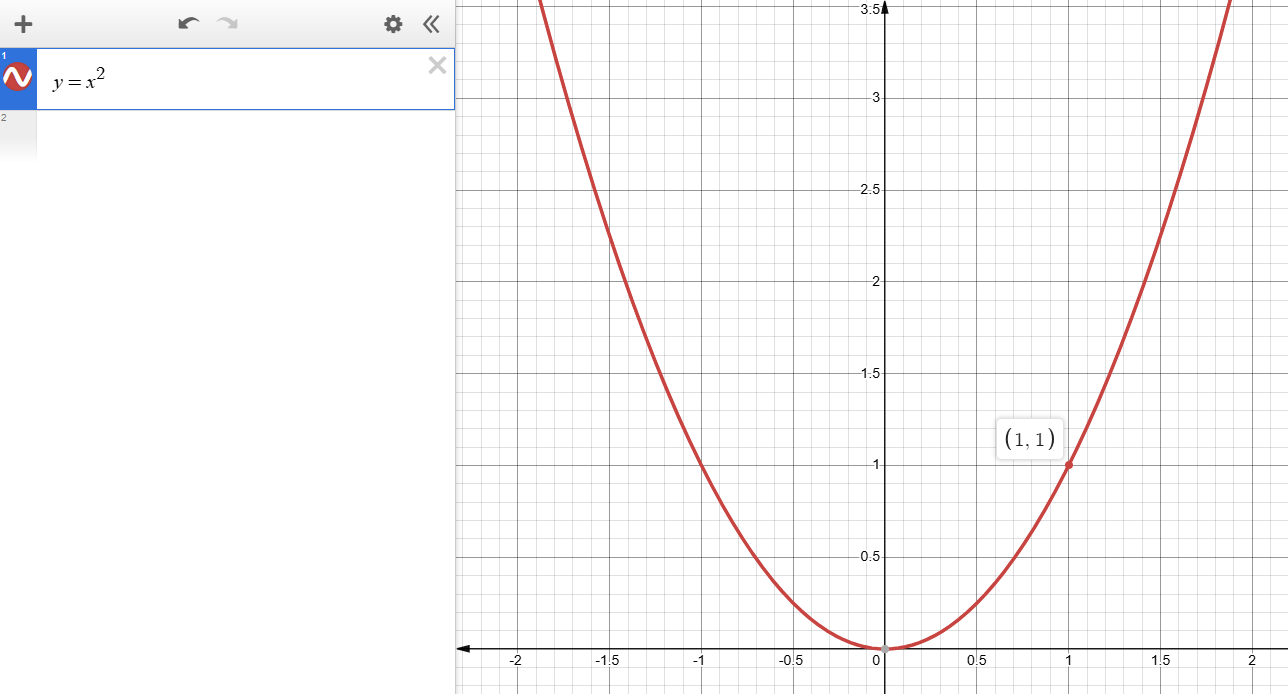
定义域:-∞ < x < ∞
值域:0 ≤ y < ∞
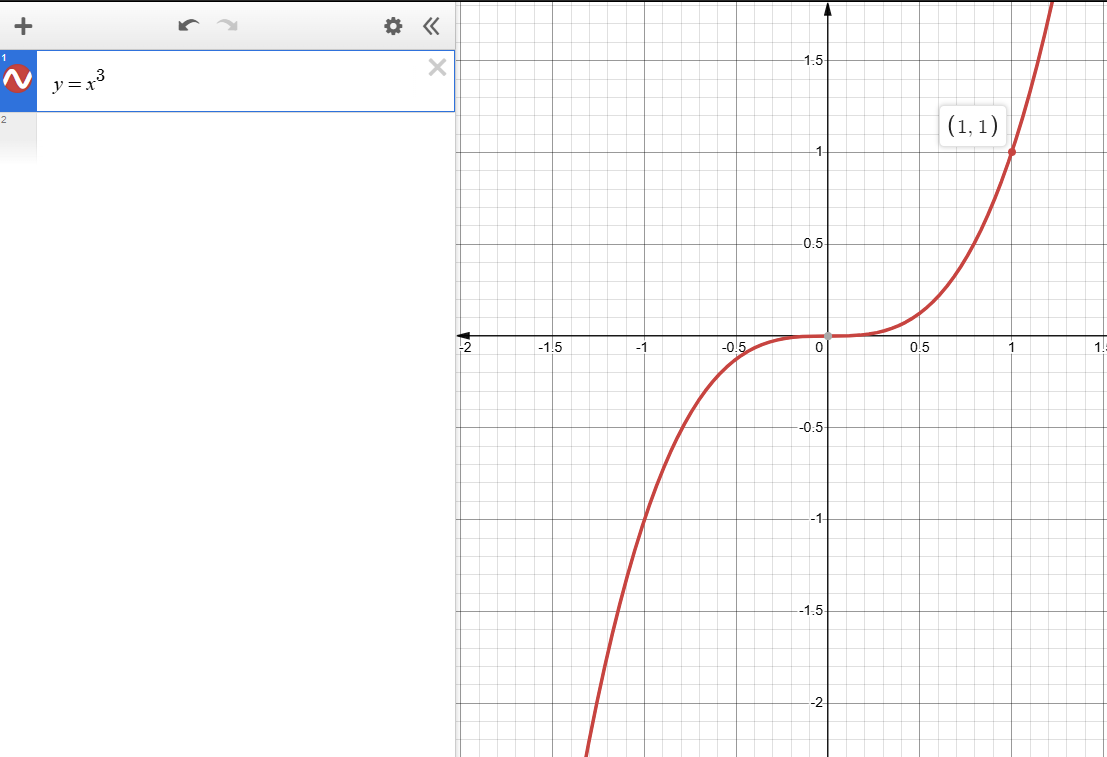
定义域:-∞ < x < ∞
值域:-∞ < y < ∞
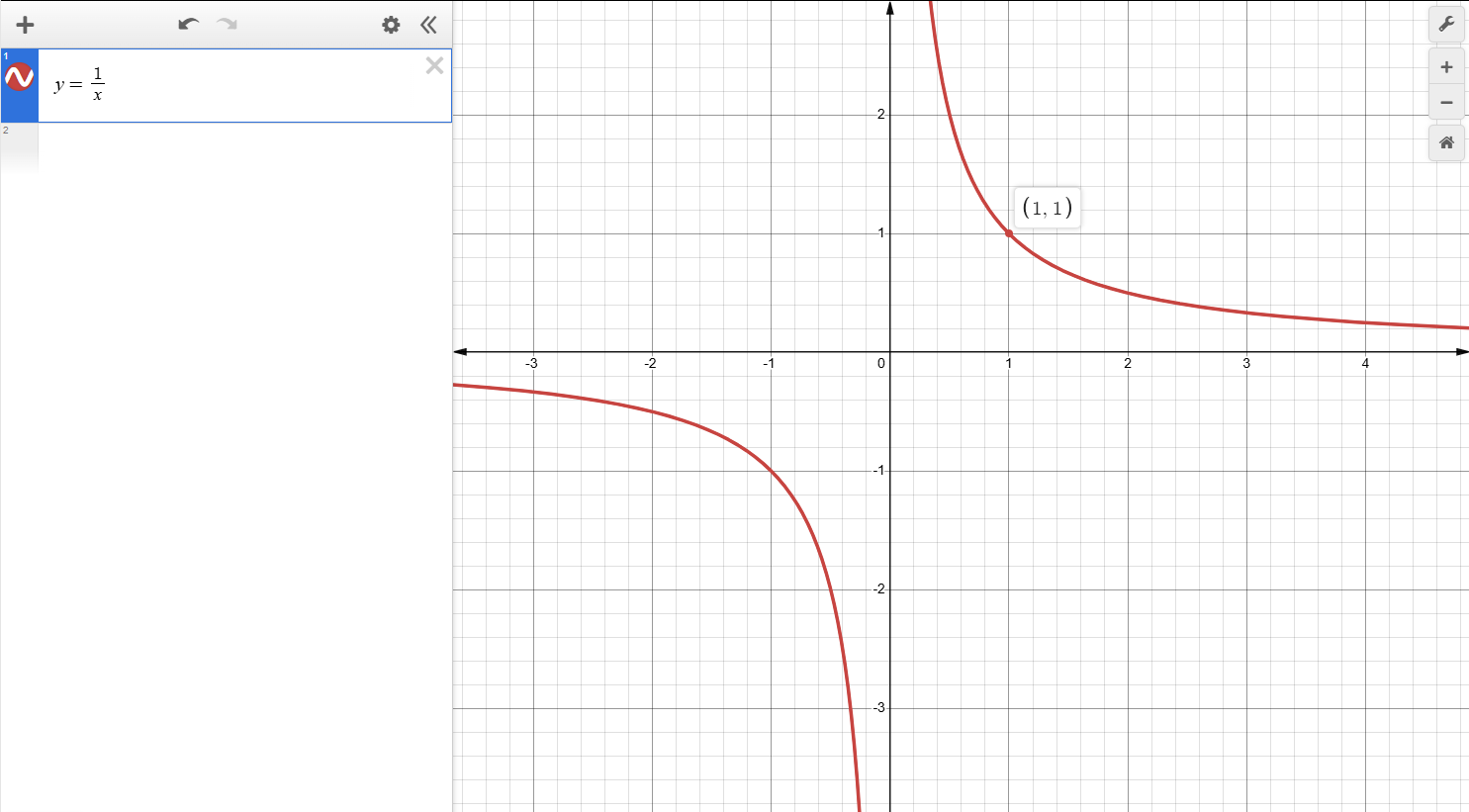
定义域:x ≠ 0
值域:y ≠ 0
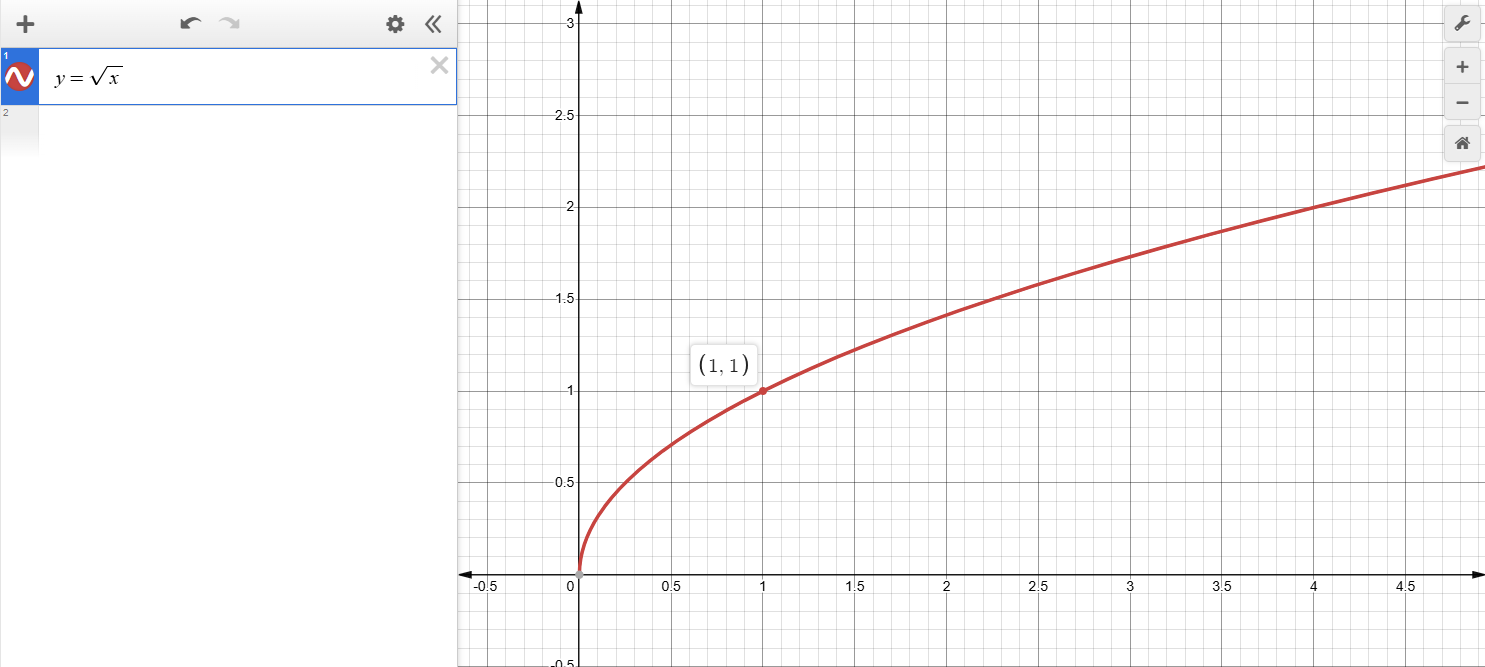
定义域:0 ≤ x < ∞
值域:0 ≤ y < ∞
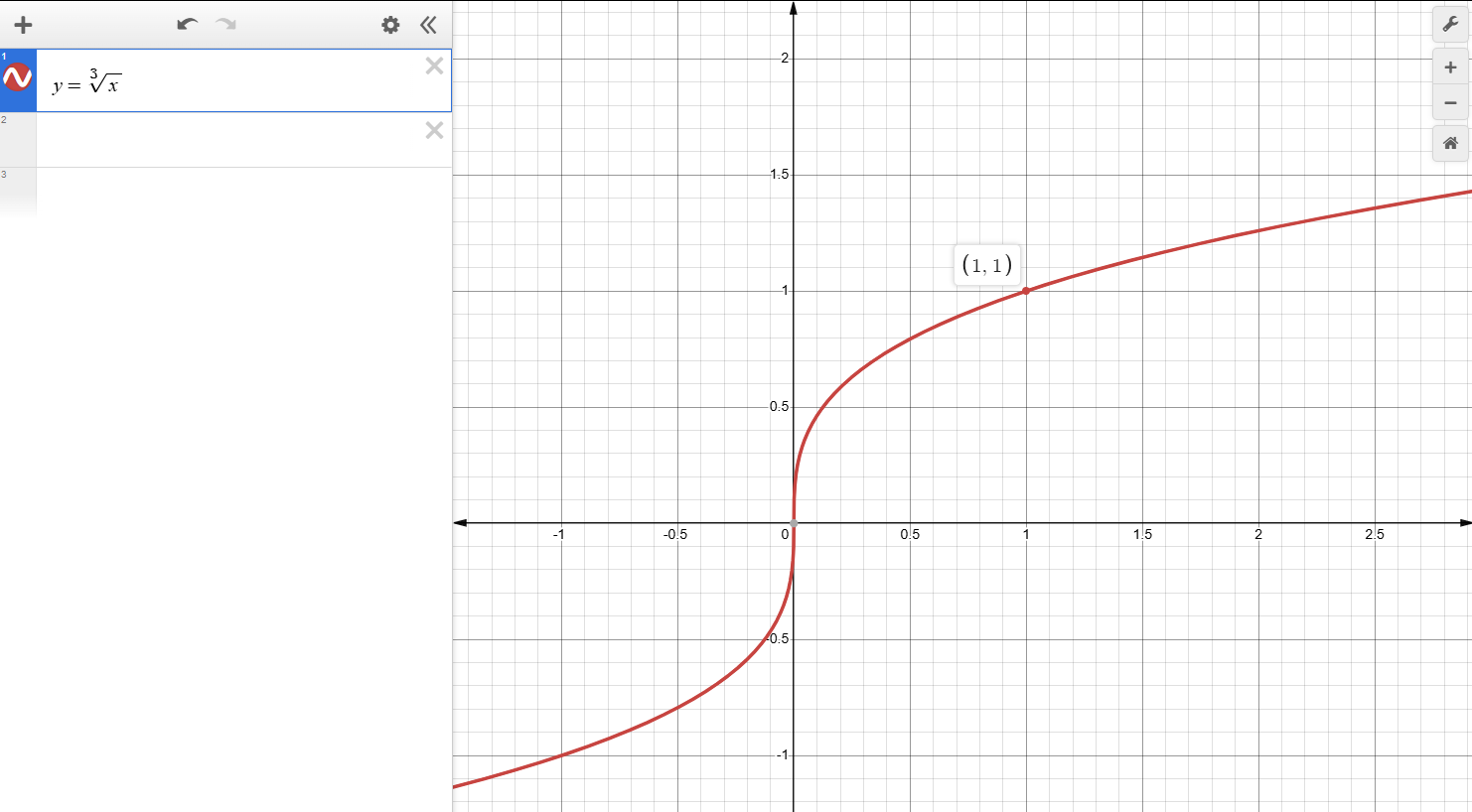
定义域:-∞ < x < ∞
值域:-∞ < y < ∞
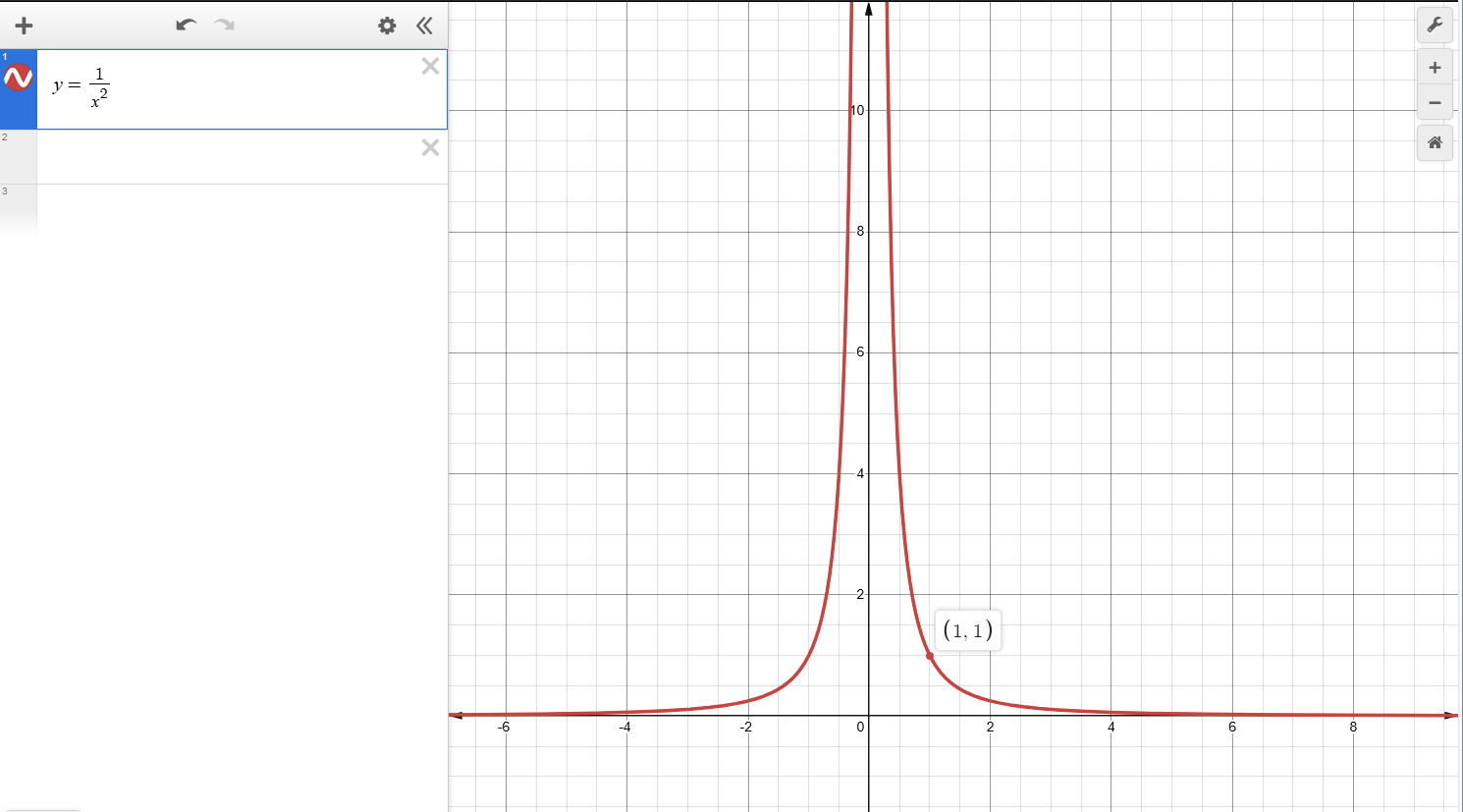
定义域:x ≠ 0
值域:y > 0
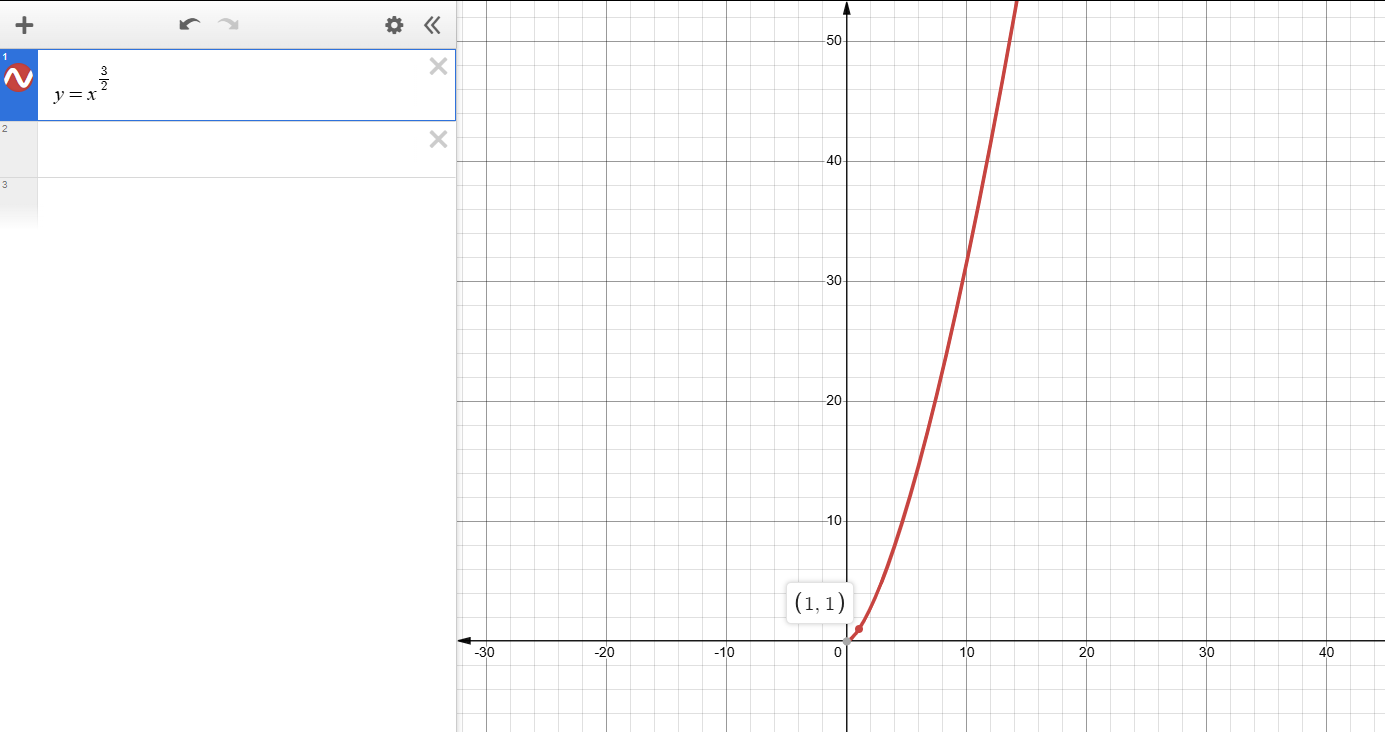
定义域:0 ≤ x < ∞
值域:0 ≤ y < ∞
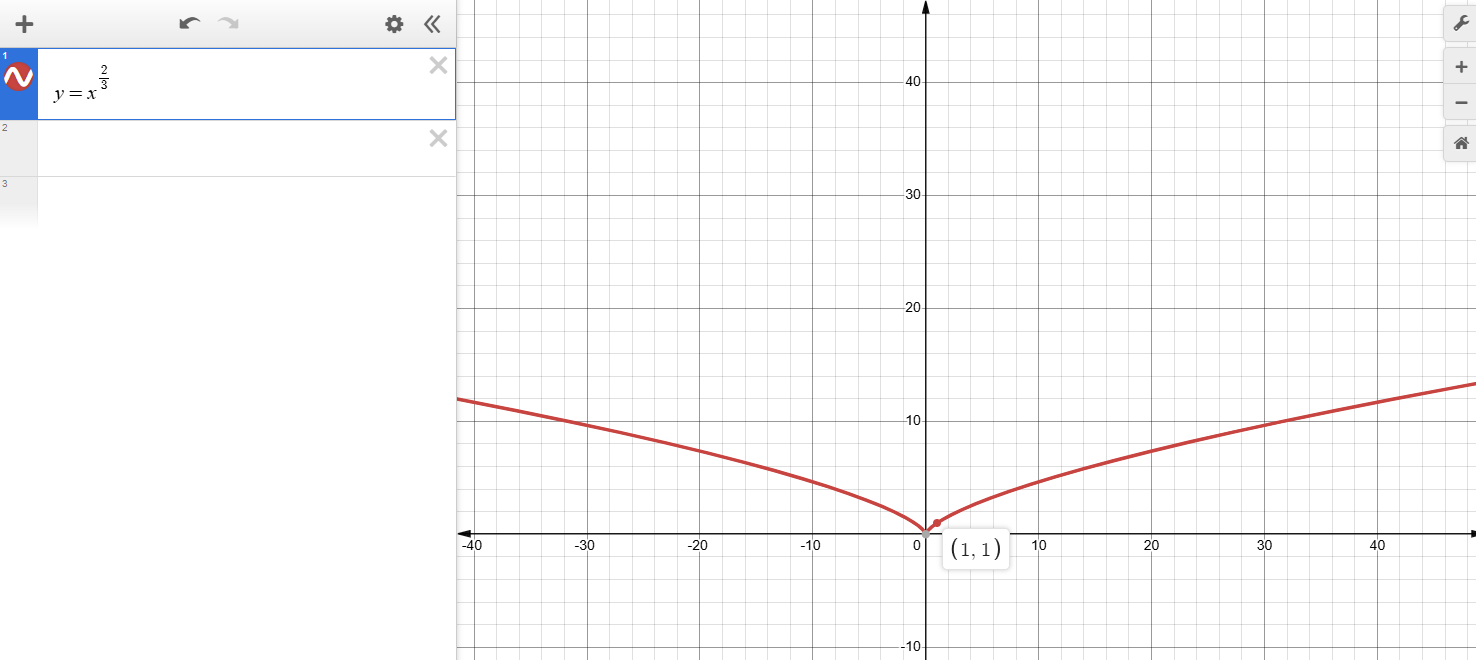
定义域:-∞ < x < ∞
值域:0 ≤ y < ∞
以上图示均为有用的幂函数。
2.4 增函数与减函数
如果当你从左走向右时,函数图形是往上爬或升高的,我们就说该函数是增函数。如果当你从左走向右时,函数的图形是下降或下落的,则该函数就是减函数。文章将在3.3节给出增函数、减函数正式定义。此节学习怎样找出函数是增的区间以及函数是减的区间。以下是来自幂函数的例子。
| 函数 | 增区间 | 减区间 |
|---|---|---|
|
|
|
|
| 不存在 |
| 不存在 |
|
|
|
|
| 不存在 | ||
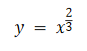 |
|
2.5 偶函数和奇函数:对称性
偶函数和奇函数的图形具有对称性的表征。
定义:偶函数、奇函数
函数y = f(x) 是
x的偶函数,如果 f(-x) = f(x),
x的奇函数,如果 f(-x) = -f(x),
对该函数定义域中任何x都成立。
偶和奇名称来自x的幂次。如果y是x的偶数次幂,如 或
,那么它们就是x的偶函数(因为
)。如果y是x的奇数次幂,如y = x或
,那么它们就是x的奇函数(因为
)。
偶函数的图形是关于y轴对称的。因为f(-x) = f(x),点(x, y)位于该图形上当且仅当(-x, y)也位于该图形上。如下图(a)。
(a)(偶函数)的图形是关于y轴对称的。
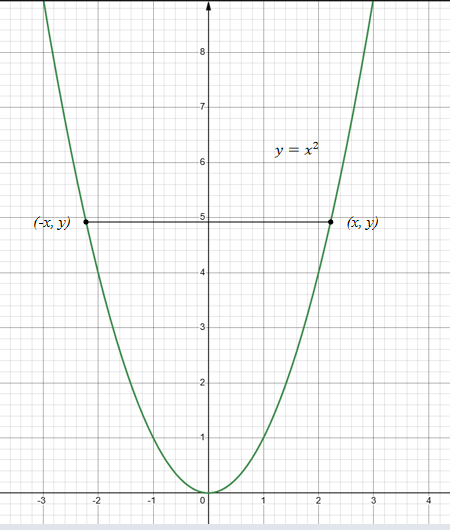
(b)(奇函数)的图形是关于原点对称的。
奇函数的图形是关于原点对称的。因为f(-x) = -f(x),点(x, y)位于该图形上当且仅当(-x, -y)也位于该图形上(b)。等价地,图形关于原点对称,如果把该图形绕原点转180°仍保持图形不变。
例4 识别偶函数和奇函数
偶函数,
对所有的x;关于y轴对称。
偶函数,
对所有的x;关于y轴对称。
奇函数,(-x) = -x 对所有的x;关于原点对称。
非奇非偶函数:f(-x) = -x + 1,但是-f(x) = -x - 1,两者不等;
(-x) + 1 ≠ x + 1,对所有的x≠0
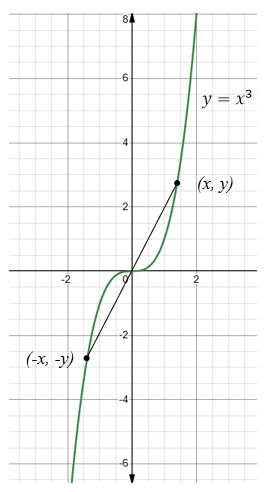
(a)当我们把常数项1加到函数上,所得到的函数
仍为偶函数,而且其图形仍关于y轴对称。
(b)当我们把常数项1加到函数上,所得到的函数
不再是奇函数了,其关于原点的对称性也没有了。
用画图形识别偶函数和奇函数是很有效的。一旦知道y轴一边的函数类型的图形,就自动知道函数在y轴另一边的图形。
2.6 分段定义的函数
可通过在定义域的不同部分用不同的公式来定义函数。
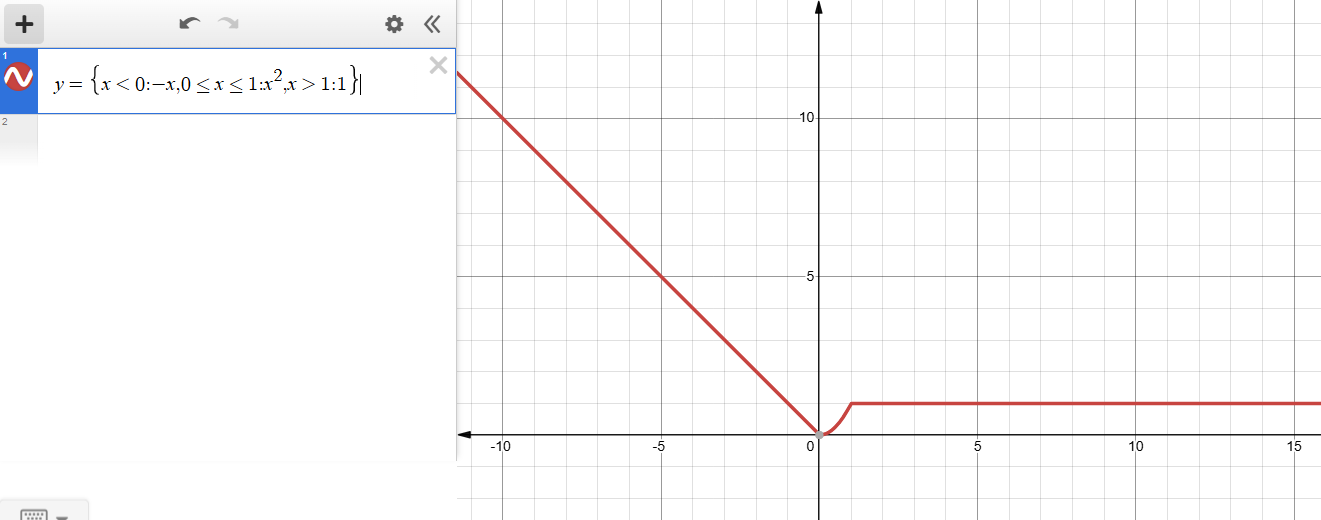
例5(画分段定义函数的图形) 画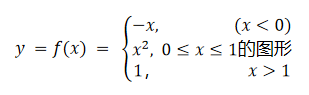
解:f值由三个不同公式给出:y = -x 当 x < 0, 当0≤x≤1,以及y = 1当 x > 1。但是,该函数只是一个函数,其定义域是整个实数集。如下图所示。
例6(写出分段定义的函数的公式) 写出函数y = f(x)的公式,该函数由下图的两段直线段组成。
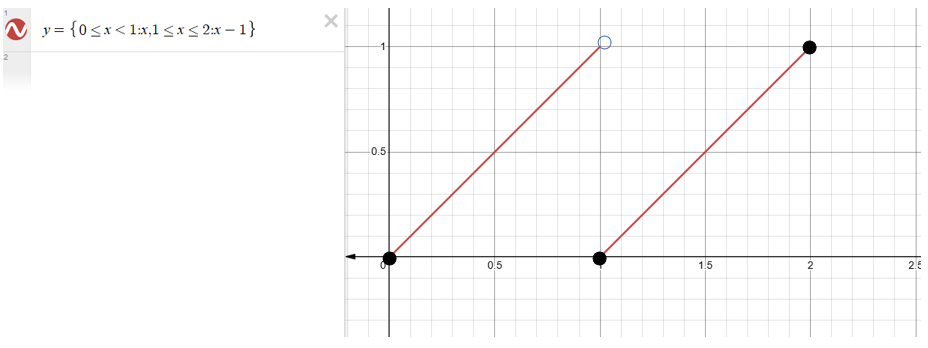
左边线段包含(0,0)但不包含(1,1);右边线段包含它的两个端点。
解:从(0,0)到(1,1)和从(1,0)到(2,1)的线段求得公式,按例5的样子把它们合到一起。
从(0,0)到(1,1)的线段:过(0,0)和(1,1)的直线的斜率为而y-截距 b=0。该直线斜率 - 截距方程为y = x。从(0, 0)到(1,1)的包含(0,0)而不包含(1,1)的线段是函数y = x限制在半开区间0 ≤ x < 1上的图形,即: y = x,0 ≤ x < 1
从(1,0)到(2,1)的线段:过(1,0)和(2,1)的直线的斜率为,并过点(1,0)。该直线相应的点-斜式方程为:y = 1(x-1) + 0 或 y = x - 1。
包含端点在内的从(1, 0)到(2,1)的线段是函数y=x-1限制在闭区间1≤x≤2上的图形,即
y = x - 1,1 ≤ x ≤ 2。
分段表达的公式 联合两段图形公式,得到:
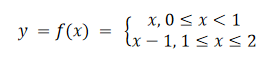
2.7 绝对值函数
绝对值函数 y = |x|是由公式
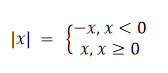
来分段定义的。
注意:,不要写成
,除非已知a≥0。
注意:绝对值的性质
1、
2、
3、
4、
证明(1):
绝对值的对称性。
分两种情况:
① 若a ≥ 0,则-a ≤ 0,有定义| -a | = -(-a) = a(因为-a ≤ 0),而|a| = a,所以|-a| = |a|。
② 若a < 0,则-a>0,有定义|-a| = -a(因为-a > 0),而|a| = -a(因为a < 0),所以|-a| = |a|。
证明(2):
乘积的绝对值。
分情况讨论符号:
情况 1:a≥0 且 b≥0。则 ab≥0,所以 ∣ab∣=ab=∣a∣⋅∣b∣。
情况 2:a≥0且 b<0。则 ab≤0,所以 ∣ab∣=−(ab)=a(−b)。
由定义:∣a∣=a(因为 a≥0),∣b∣=−b(因为 b<0),∣ab∣=a⋅(−b)=∣a∣⋅∣b∣。
情况 3:a<0且 b≥0。同情况 2,∣ab∣=∣ba∣=∣b∣⋅∣a∣=∣a∣⋅∣b∣(由对称性)。
情况 4:a<0且 b<0。则 ab>0,所以 ∣ab∣=ab。由定义:∣a∣=−a,∣b∣=−b,因此 ∣a∣⋅∣b∣=(−a)(−b)=ab。故 ∣ab∣=∣a∣⋅∣b∣。
证明(3):
商的绝对值。
先证:
若b > 0,则 ,所以
(因为|b| = b)。
若b < 0,则 ,所以
。而|b| = -b,因此
,故
再由乘积性质:
证明(4):
三角不等式(使用平方函数,因其在非负区间单调增)
计算
计算
比较二者,由于,有
,因此:
因为 和
, 且平方函数在[0, +∞)上单调增,所以:
绝对值函数是偶函数(如下图),因而其图形是关于y轴对称的。因为符号表示a的非负平方根,所以|x|的另一种定义是
2.8 怎样移位图形
往上移位函数y = f(x)的图形,加一正数常数到公式的右边;
往下移位函数y = f(x)的图形,加一负数常数到公式的右边。
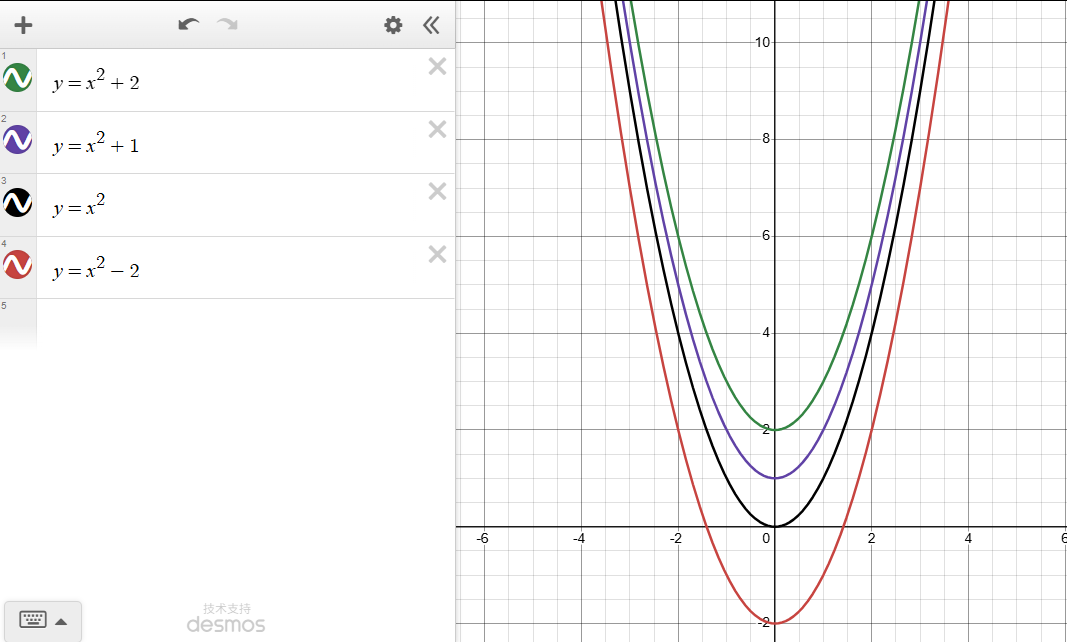
例7(垂直移位图形) 在公式 的右端加1就得到
,把图形往上移位1个单位(如下图)。在公式
的右端加-2就得到
,把图形往下移位2个单位(如下图)。
为向左移位y=f(x)的图形,加一正数常数到x;为向右移位y=f(x)的图形,加一负数常数到x。
例8(水平移位图形) 在 中的x加上3得到
,图形向左移位3个单位(如下图)。在
中的x加上-2得到
,图形向右移位2个单位(如下图)。
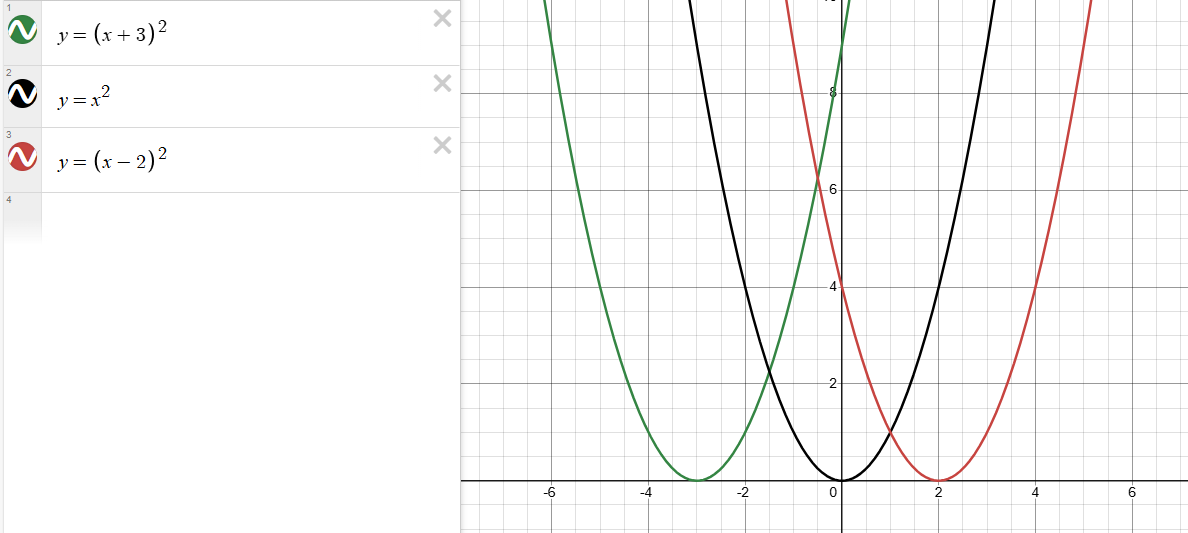
可得到如下移位公式:
垂直移位:
y = f(x) + k
若k > 0,则向上移位k个单位;
若k < 0,则向下移位|k|个单位;
水平移位:
y = f(x+h)
若 h > 0,则向左移位h个单位;
若 h < 0,则向右移位|h|个单位;
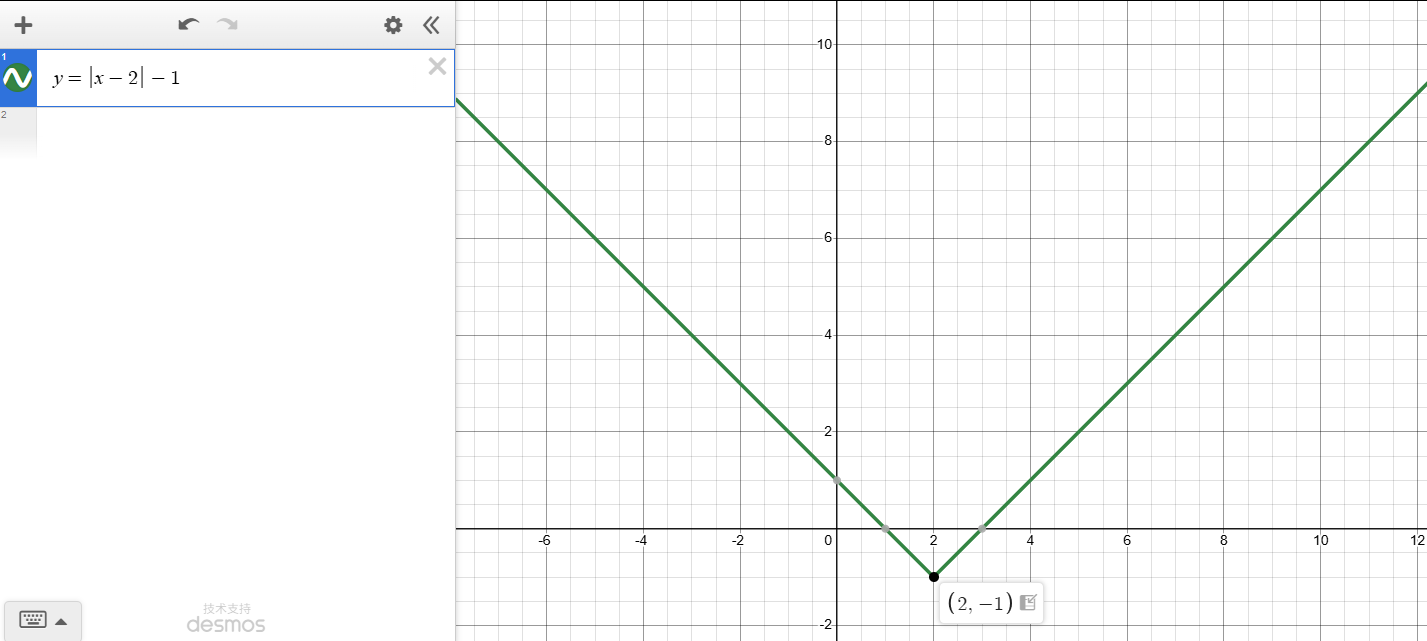
例9(组合移位) 求f(x) = |x - 2| - 1的定义域和值域,并画出图形。
解:f的图形是绝对值函数水平向右移位2个单位,再垂直向下移位一个单位(如下图)。f的定义域是(-∞,∞),其值域为[-1, ∞)。
2.9 复合函数
假定函数g的某些输出可作为函数f的输入。那么我们可以构造一个新函数把g和f联系起来,该新函数输入x是g的输出,从而输出为数f(g(x)),如图所示。

(每当一个函数在x处的值在另一函数的定义域中,这两个函数就可以在x处复合。这种复合函数记作f·g。)
函数f(g(x))是g和f的复合函数。这是按先g后f的次序复合g和f的。这个复合函数通常的“独立”记号是f·g。f·g在x处的值是(f·g)(x)=f(g(x))。注意在记号f·g中,我们首先把g作用到输入变量然后再作用f。
例10(把函数作为复合函数进行审阅) 例2中函数 可以设想为首先计算
,紧接着对结果开平方根。函数y是函数g(x) =
和函数f(x) =
的复合函数。注意
不能为负。复合函数的定义域为[-1, 1]。
例11(求复合函数的公式并求值) 求f(g(x))的公式,若 ,而
,然后求f(g(2))。
解:为求f(g(x)),我们用g(x)的表达式代替公式f(x) = x - 7 中的 x。
然后在x处带入2求出f(g(2))的值:
习题2
求函数的公式
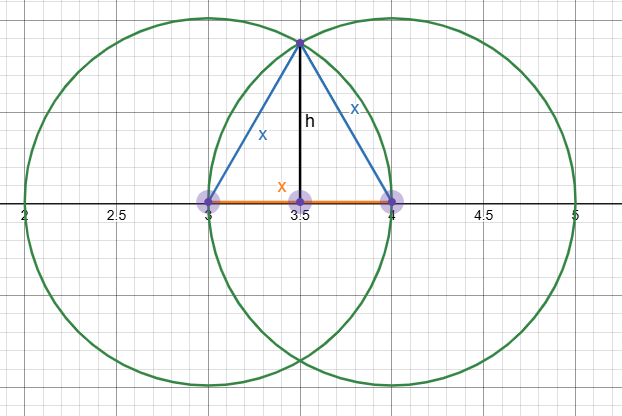
1. 把等边三角形的面积和周长表示为该三角形边长x的函数。

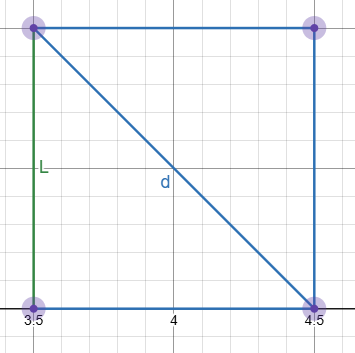
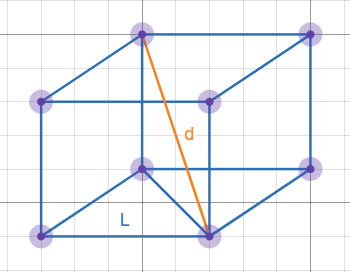
2. 把正方形的边长表示为该正方形对角线长度d的函数,然后把该正方形的面积表示为对角线长度的函数。
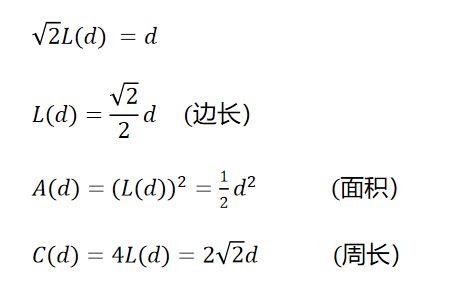
3. 把立方体的棱边长表示为该立方体对角线长度d的函数,然后把该立方体的表面积和体积表示为对角线长度的函数。
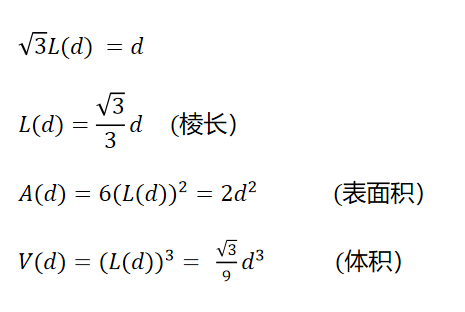
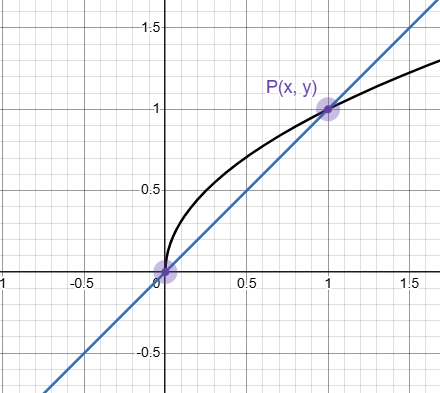
4. 第一象限中的点P位于函数 的图形上,把点P的坐标表示为连接点P和原点的直线的斜率的函数。

在题5和6中,哪些图是x的函数,哪些不是?对回答给出理由。
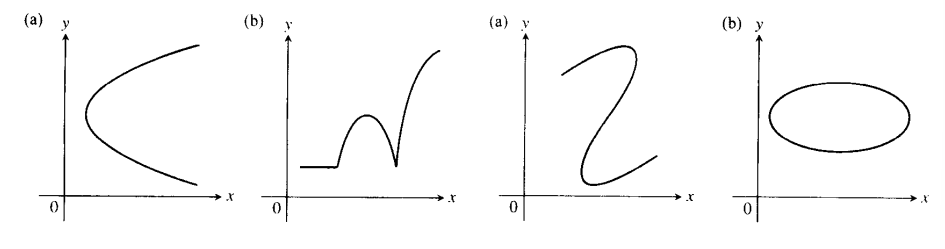
根据函数的定义,对于定义域内的每一个x值,都有唯一确定的y值与之对应。
判断一个图像是否为x的函数,采用垂直于x轴的直线检验法(竖线检验法):若任意一条垂直于x轴的直线与图像最多有一个交点,则该图像是x的函数;若存在一条垂直于x轴的直线与图像有两个或两个以上交点,则不是x的函数。
(a)明显不是;(b)是的;(c)不是;(d)不是。
定义域和值域
在题7-10中,求每个函数的定义域和值域。
7. (a)
定义域
对于,由于
对任何实数 x 都有定义(平方运算在实数范围内始终有效),且常数项 1 不影响定义域。
因此,定义域为 所有实数,即 R 或用区间表示为 (−∞,+∞)。
值域
分析函数: 对所有实数 x 成立(因为平方结果非负)。
因此,。当 x=0时,f(x)取最小值 1(即 f(0)=1)。
当 ∣x∣增大时,增大,f(x)也增大且无上界(例如,x=1时 f(1)=2,x=2时 f(2)=5,依此类推)。因此,值域为所有大于或等于 1 的实数,即 [1,+∞)。
(b)