(nice!!!)(LeetCode 每日一题) 1277. 统计全为 1 的正方形子矩阵 (动态规划)
题目:1277. 统计全为 1 的正方形子矩阵

思路:动态规划dp,时间复杂度0(nm)。
考虑每个点,作为正方形的右下角的情况,有多少个正方形。这就需要知道最大可能的正方形长度,假设点(x,y)的最大可能的正方形长度是a,那么就有a个。
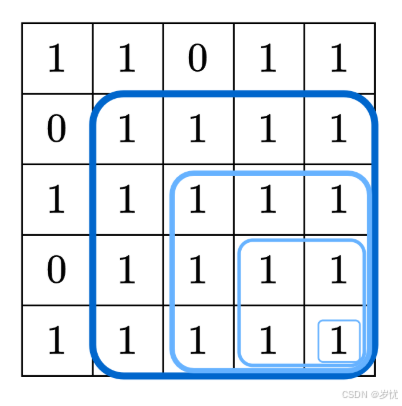
而如何找到最大的长度,其实可以由(x-1,y)、(x-1,y-1)、(x,y-1)这三个点的最大长度推出,其实就是三者的最大长度的最小值+1,即:v[i+1][j+1]=min({v[i][j],v[i+1][j],v[i][j+1]})+1。这里用到的就是动态规划
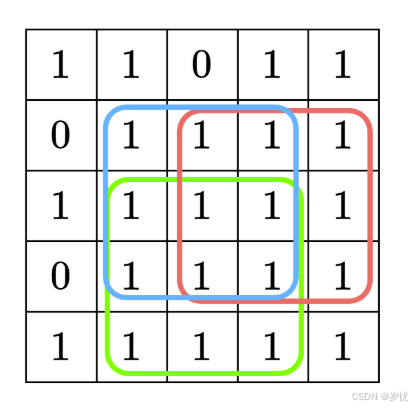
大神的思路
C++版本:
class Solution {
public:int countSquares(vector<vector<int>>& matrix) {int n=matrix.size(),m=matrix[0].size();vector<vector<int>> v(n+1,vector<int>(m+1,0));int ans=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(matrix[i][j]==1){v[i+1][j+1]=min({v[i][j],v[i+1][j],v[i][j+1]})+1;ans+=v[i+1][j+1];}}}return ans;}
};
JAVA版本:
class Solution {public int countSquares(int[][] matrix) {int n=matrix.length,m=matrix[0].length;int[][] v=new int[n+1][m+1];int ans=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(matrix[i][j]==1){v[i+1][j+1]=Math.min(Math.min(v[i][j],v[i+1][j]),v[i][j+1])+1;ans+=v[i+1][j+1];}}}return ans;}
}
GO版本:
func countSquares(matrix [][]int) int {n,m:=len(matrix),len(matrix[0])v:=make([][]int,n+1)for i:=range v {v[i]=make([]int,m+1)}ans:=0for i:=0;i<n;i++ {for j:=0;j<m;j++ {if matrix[i][j]==1 {v[i+1][j+1]=min(min(v[i][j],v[i+1][j]),v[i][j+1])+1ans+=v[i+1][j+1]}}}return ans}
