算法——质数筛法

前言

这些是数学相关的算法，理解一下思路，记一下模板代码即可，多用于数据处理，即解题中的某一步。

质数概念：

• 质数，又称素数，即约数只有1以及它本身的数。
• 0和1既不是质数也不是合数。

比如在自然数中，分三部分：

1. 0和1
2. 质数
3. 合数

就是说如果有一个除了0和1的数，它不是质数就是合数。

筛质数:

将0—n之间的质数筛选出来，并保存到一个数组中或者直接输出。

方法（1-3时间复杂度逐渐降低）:

(1)朴素方法

根据定义，因为质数除了1和本身之外没有其他约数，所以判断n是否为质数根据定义直接判断从2到n-1是否存在n的约数即可。代码如下:

bool isPrime( int n){
if(n<2){return 0;//0和1不是质数
}
int tmp =n-1;//判浙到n-1
for(int i= 2;i <=tmp; i++){if(n %i== 0){return 0;//n与比它小的数相除，除的尽则不是质数}return 1;//都除不尽，是质数
}
for(int i=2;i<=n;i++){if(isPrime(i)==1){printf(“%d ”,i);}
}

优化1：

思考一个数去除以比它的一半还要大的数，一定除不尽的，这还用判断吗???
因此，只需要除到n/2。

bool isPrime( int n){
if(n<2){return 0;//0和1不是质数
}
int tmp =n/2;//判浙到n/2
for(int i= 2;i <=tmp; i++){if(n %i== 0){return 0;//n与比它小的数相除，除的尽则不是质数}return 1;//都除不尽，是质数
}
for(int i=2;i<=n;i++){if(isPrime(i)==1){printf(“%d ”,i);}
}

时间复杂度是O(n^2)

优化2：

一个数若可以进行因数分解，那么分解时得到的两个数一定是一个小于等于sqrt(n)，一个大于等于sqrt(n)，据此，上述代码中并不需要遍历到n-1，遍历到sqrt(n)即可，因为若sqrt(n)左侧找不到约数，那么右侧也一定找不到约数。因此只要从2枚举到 √n即可。

bool isPrime( int n){
if(n<2){return 0;//0和1不是质数
}
int tmp =sqrt(n);//sqrt()是计算一个非负实数的平方根
for(int i= 2;i <=tmp; i++){if(n %i== 0){return 0;//能整除，是合数}return 1;//都除不尽，是质数
}
for(int i=2;i<=n;i++){if(isPrime(i)==1){printf(“%d ”,i);}
}

时间复杂度是O(n^(3/2))

(2)埃氏筛法

埃拉托色尼选筛法(the Sieve of Eratosthenes)简称埃氏筛法，是古希腊数学家埃拉托色尼提出的一种筛选法。

基本原理:

一个合数总是可以分解成若干个质数的乘积，那么如果把质数(最初只知道2是质数)的倍数都去掉，那么剩下的就是质数了。

步骤:

1. 先把1删除(1既不是质数也不是合数)
2. 读取数组中当前最小的数2，然后把2的倍数删去
3. 读取数组中当前最小的数3，然后把3的倍数删去A读取数组中当前最小的数5，然后把5的倍数删去
4. … …

n. 读取数组中当前最小的状态为true的数n，然后把n的倍数删去

代码思路：

代码思路:
1、状态初始化。
2、从2开始，判断是否是质数，保存2，遍历比n小的所有2的倍数，状态
置false。
3、判断是否是质数，保存3，遍历下一一个质数即3的倍数，并将状态置false。

int n=100000;
int isPrime[100005];//1为质数，0不是质数 
int prime[100005];
int k=0;
int main(){for(int i=2;i<=n;i++){isPrime[i]=1;//假设都是质数 }for(int i=2;i<=n;i++){//开始遍历 O(n)if(isPrime[i]==1){k++;//prime[k]=i;//是质数保存到质数数组里面 for(int j=i*2;j<=n;j+=i){//遍历j的倍数 O(1og*1ogn)isPrime[j]=0;//j的倍数必然不是质数 }}}return 0；
} 

埃氏做了许多无用功一个数会被筛到好几次，比如6是2和3的倍数，则被到了两次最后的时间复杂度是O(nloglogn)。
如果我们在筛选时，对每一个数只筛一遍，那么这个时间复杂度将会怎样变化呢?

(3)欧拉筛法

算术基本定理(唯一分解定理)任何合数都能表示为若干质数的乘积且该分解因式是唯一的。(不考虑顺序性)

原理:

规定每个合数只会被它最小的质因数筛去。(后面的质因数直接跳过)，这个最小的质因式必定小于它本身。

代码：

int n=10000;
int isPrime[100005];//1为质数，0不是质数 
int prime[100005];
int k=0;
int x;
int main(){for(int i=2;i<=n;i++){isPrime[i]=1;//假设都是质数 }for(int i=2;i<=n;i++){//枚举需要判断的每个数+枚举倍数 if(isPrime[i]==1){k++;//prime[k]=i;//是质数保存到质数数组里面 }//枚举质数表——质数表的数都是有序的（升序）for(int j=1;j<=k;j++){x=i*prime[j];//质数表里面的倍数一定不是质数 if(x>n){//超出筛选范围结束 break;}isPrime[x]=0;//倍数设为0if(i%prime[j]==0){//保证每个合数被其最小质因数给筛掉 //保证了只能筛选到以prime[j]为最小质因数的数//就是说，i之前被prime[j]筛选过，prime[j]是升序的//如果继续循环让i乘上后面的质数，得到的合数就不是被prime[j]筛掉的 break;}} }return 0;
} 

时间复杂度是O(n)。线性时间复杂度，线性筛

图片示例

i枚举倍数

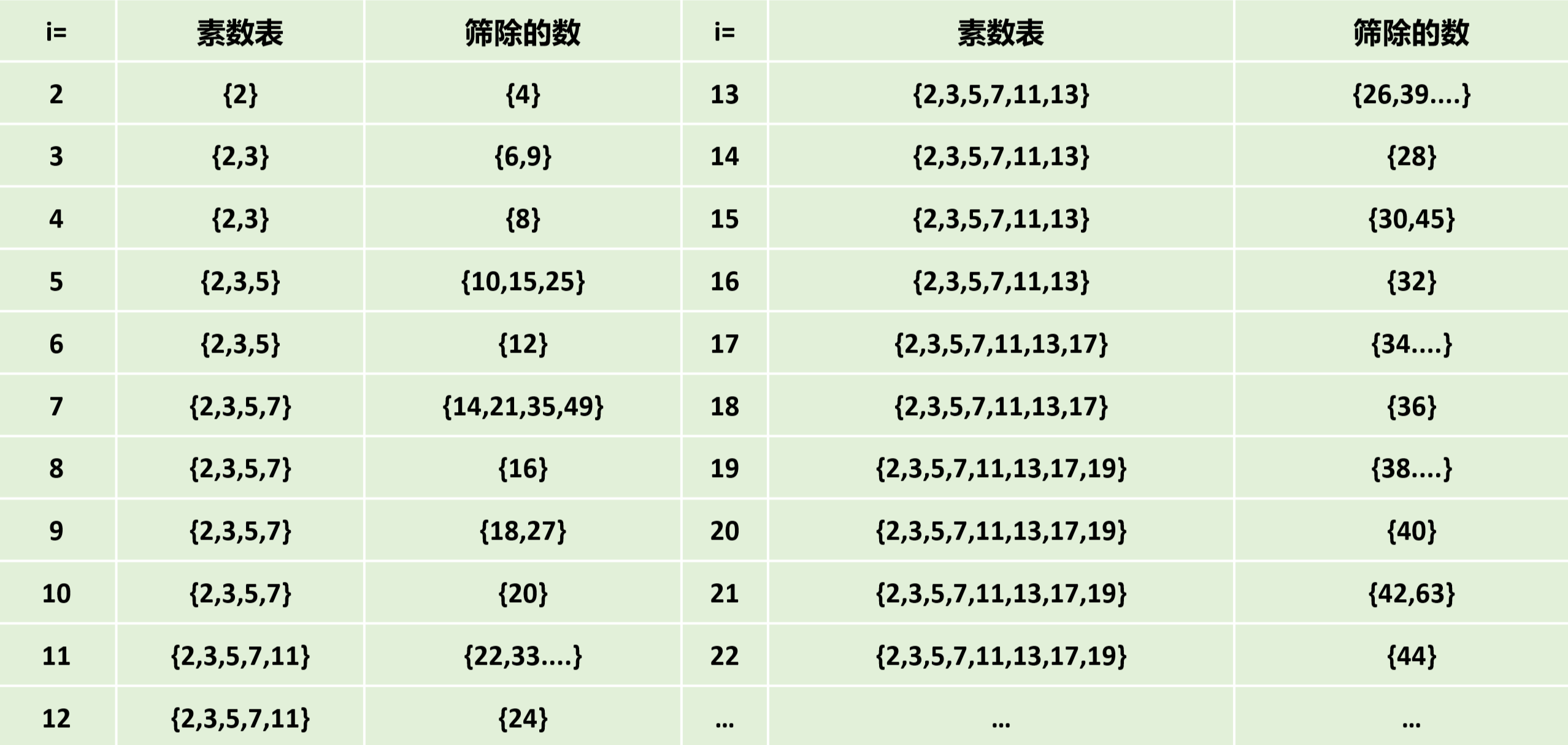
• 为什么在i=4时只筛掉8？不筛掉12？

答：用上面示例过的代码来说，此时来到这一步i%prime[j]==0，即4除以2的余数为0，意味着2是4的最小质因数，退出是为了确保每个合数只被其最小质因数标记一次，如果不退出，筛掉12（4×3），那么当i=6时，又会筛掉一次12（6×2），这样就达不到线性时间复杂度了，因为12的最小质因数为2，由i=6时筛掉。就是说，当遇到最小质因数时，停止当前i枚举倍数。

板子题

https://www.luogu.org/problemnew/show/P3383

看数据范围，选择筛法。其实直接把欧拉筛法啃下来，以后叫你找质数直接无脑欧拉筛法，因为它是最快的，不理解背也要背下来